
- •Глава1. Проблема аппроксимации
- •§1. Полиномиальная апппроксимация
- •§2. Интерполяционный полином в форме Лагранжа
- •§3. Интерполяционный полином в форме Ньютона
- •§4. Аппроксимация сплайнами
- •§5. Метод наименьших квадратов
- •§6. Полиномиальная интерполяция с кратными узлами
- •§7. Свойства разделенных разностей
- •§8. Задача Чебышева. Разрешимость системы
- •§9. Теорема Чебышева
- •§10. Многочлены Чебышева
- •Глава2. Численное дифференцирование
- •Глава3. Численное интегрирование
- •§1. Интерполяционные квадратурные формулы
- •1.Интерполяционные квадратурные формулы
- •2.Интерполяционные квадратурные формулы наилучшей алгебраической точности
- •3.Ортогональные многочлены и их свойства
- •§2. Применение квадратурных формул
- •§3. Метод Монте-Карло (метод статистических испытаний)
- •§4. Правило Рунге практической оценки погрешности
- •Глава4. Алгебраическая проблема собсвенных значений
- •§1. Ортогональные матрицы
- •1.Ортогональные матрицы
- •2.Матрица элементарного поворота
- •§2. Вариационное свойство собственных значений
- •§3. Приведение симметричной матрицы к диагональному виду
- •§4. Сингулярное разложение матрицы
- •§5. Сопряженная матрица
- •§6. Частная спектральная задача
- •1.Вариационный метод
- •2.Степенной метод
- •§7. Метод максимизации столбцов
- •1.Максимизация первого столбца
- •2.Алгоритм сингулярного разложения
- •3.Главное собственное число
- •§8. Метод вращения
§3. Интерполяционный полином в форме Ньютона
Рассматривается функция f(х), заданная дискретно в узлах х0...хn. Ставится задача её аппроксимации по этим данным.
Введём понятие разделённых разностей:
1-ого порядка -
![]()
2-ого порядка -
![]()
k-ого порядка -
![]()
нулевого порядка
-
![]()
Тогда:
![]() ,
,
![]()
....................
![]()
....................
![]()
Из первого равенства получим:
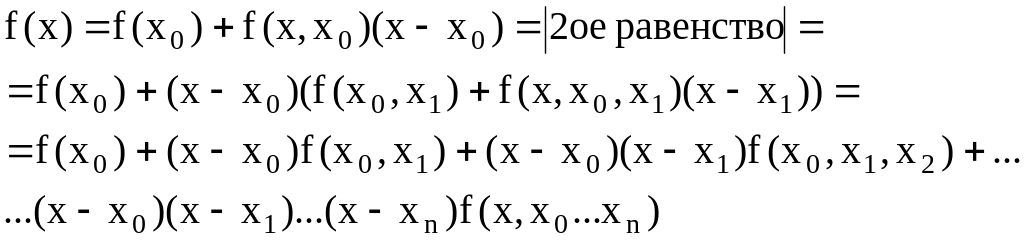
Обозначим все слагаемые, кроме последнего как Рn(х), последнее - Rn(х).
Рn(х) – интерполяционный полином (т.к. он порядка n и совпадает в узлах с f(х)) Ньютона.

Следствие:
![]()
§4. Аппроксимация сплайнами
Рассматривается
задача приближения функции f(х) на
некотором интервале по её значениям в
узлах х0...хn
(хk<
хk+1
![]()
К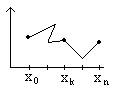 усочно-линейная
функция, совпадающая в узлах с f(х) –
линейный
сплайн.
усочно-линейная
функция, совпадающая в узлах с f(х) –
линейный
сплайн.
Обозначим разбиение {x0…xn} как Т.
Сплайн
![]() порядка m
для функции f(х) по разбиению Т –
кусочно-полиномиальная функция, если:
порядка m
для функции f(х) по разбиению Т –
кусочно-полиномиальная функция, если:
1) на каждом из
отрезков [xk-1,
xk]
![]() это многочлен
m-ого порядка
это многочлен
m-ого порядка
2) в узлах совпадает
с функцией f(х):
![]()
3) во внутренних
узлах (х1...хn-1)
эта функция непрерывна вместе со своими
производными до (m-1)-ого порядка
![]() .
.
Построение сплайна
Обозначим многочлен, который необходимо найти на [xk-1, xk] как:
![]() (m+1
коэффициент).
(m+1
коэффициент).
Из условия 2) для сплайна => (n+1) уравнение.
Из условия 3) => (n-1) уравнение для каждой из m функций.
Итого всего уравнений для сплайна: n+1+m(n-1)=n(m+1)+1-m
Всего неизвестных коэффициентов (m+1) для каждого из n отрезков, т.е. n(m+1).
Таким образом, число уравнений и искомых коэффициентов совпадает при m=1, иначе условий не хватает для нахождения коэффициентов, и требуются дополнительные условия.
Основные сплайны:
- 1-ого порядка – линейные;
- 2-ого порядка – кубические (m=3).
Для них 4n-2 уравнения и 4n коэффициентов.
В качестве двух дополнительных условий обычно задают значения производных в двух узлах.
Таким образом, функция f(х) может быть интерполирована на [x0, xn] сплайном заданного порядка.
§5. Метод наименьших квадратов
Рассмотрим некоторую
функцию
![]() .
В полиномиальной аппроксимации она
приближается по значениям в узлах
х0...хn
линейной комбинацией степеней хk
(полиномом k-ой степени).
.
В полиномиальной аппроксимации она
приближается по значениям в узлах
х0...хn
линейной комбинацией степеней хk
(полиномом k-ой степени).
Таким образом, функцию f(х) на [a,b], заданную в узлах х0...хn можно аппроксимировать некоторыми функциями φk(k), общее число которых (р+1), р≠n.
Рассмотрим некоторые употребляемые частные случаи:
1) Полиномиальная
задача: найти
для функции f(х) такую линейную комбинацию
функций φk:
![]() что их разность в некотором определенном
смысле минимальна (в случае полиномиальной
аппроксимации разность рассматривается
в узлах).
что их разность в некотором определенном
смысле минимальна (в случае полиномиальной
аппроксимации разность рассматривается
в узлах).
Рассмотрим следующее выражение:
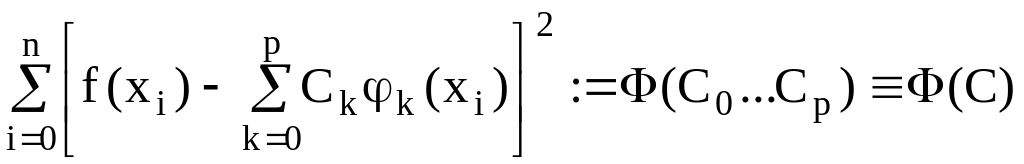
Необходимое условие
минимума функции
![]()
![]()
Таким образом, получим следующую систему уравнений:
![]()
Или:
![]()
2) Континуальная задача: аппроксимировать функцию f(х) в С [a, b] в смысле средне квадратичного.
Обозначим
![]()
Необходимое условие экстремума имеет вид:
Получим систему:
![]()
Или:
![]()
т.к.
![]() -
скалярное произведение φm
на φk
в L2
(а, b),
то:
-
скалярное произведение φm
на φk
в L2
(а, b),
то:
![]()
Определитель с матрицей А=(аkm), где аkm= (φk, φm) – определитель Грамма.
Заметим, что det
А≠0, если система
![]() линейно независима, следовательно,
наилучшее средне квадратичное приближение
существует и притом единственно.
линейно независима, следовательно,
наилучшее средне квадратичное приближение
существует и притом единственно.
Рассмотрим
подпространство
![]() (натянутое на функции φ0...φр
в пространстве L2
(а, b)).
(натянутое на функции φ0...φр
в пространстве L2
(а, b)).
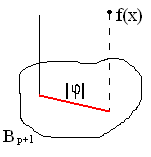
![]() - проекция f(х) на
Вр+1.
Приэтом она существует единственно,
если φk
линейно независима.
- проекция f(х) на
Вр+1.
Приэтом она существует единственно,
если φk
линейно независима.
