§6. Полиномиальная интерполяция с кратными узлами

Пусть дана дискретная функция f(х) в узлах х₀, х₁...х_m (х_k<х_k+1, ). А также заданы значения в узлах для производных функции f(х):

; S=0, 1...S_k-1. Причем

Требуется построить многочлен Q_n(х) n-ой степени, совпадающий в узлах со всеми этими значениями, т.е. получим систему:

Интерполяционный многочлен Q_n(х) определяется единственным образом. Действительно, предположим, что существует многочлен n-ой степени:

удовлетворяет условиям вышеописанной системы. Тогда их разность удовлетворяет следующим условиям:

Т.е. точки х₀...х_m – нули многочлена Р_n(х) кратности S₀...S_m соответственно. Получено: многочлен Р_n(х)≠0 степени n имеет n+1 нулей (из кратности). Отсюда, Р_n(х)≡0. Противоречие доказывает требуемое.

Таким образом, линейная алгебраическая система невырождена, и её решение находится единственным образом.

Погрешность интерполяции.

Обозначим f(х):=Q_n(х)+R_n(х).

Представим погрешность R_n в виде:

Отсюда, (1)

где S=0...S_k-1; φ(х_k)=0; k=0, 1...m (т.е. х_k – нули кратности S₀...S_m соответственно).

Выберем k из условия φ(х')=0, где х' – точка, в которой оценивается погрешность

Из уравнения φ(х')=0 получим:

Будем предполагать, что Тогда при таком выборе К и обращается в ноль в (n+2) точках (считая кратность): х₀...х_m, х'.

Следовательно, по Т. Ролля φ'(х) обращается в ноль в по крайней мере (n+1) точке.

...........................................................................

Тогда, по Т. Ролля φ⁽ⁿ⁺¹⁾(х) имеет хотя бы один нуль.

Т.е. существует g=g(х'): φ⁽ⁿ⁺¹⁾(g)=0.

Из равенства (1) получим:

Отсюда,

Т.к. х' выбрано произвольно, то последнее равенство верно при

§7. Свойства разделенных разностей

Пусть задана дискретная функция f(х) в узлах х₀...х_n (х_k < х_k+1), а также её разделенная разность k-ого порядка:

Лемма: Справедливо равенство:

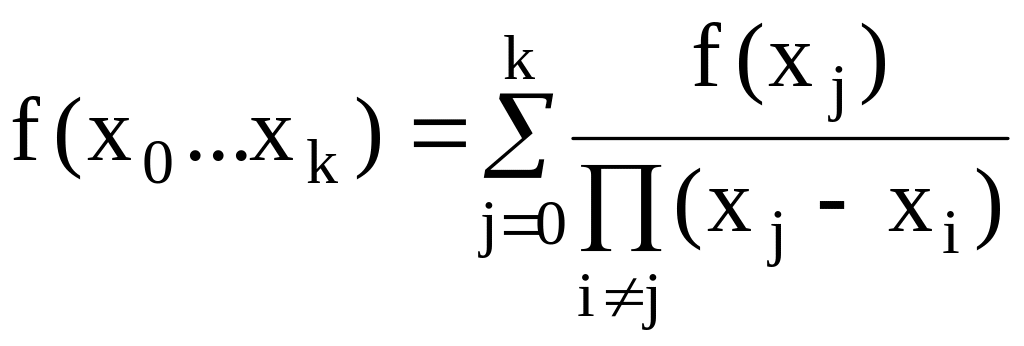
Доказательство(методом математической индукции):

При k=1:

Пусть верность равенства доказана при

Докажем для m-ого порядка:

Рассмотрим слагаемое для f(х₁):

Аналогично для остальных слагаемых.

Что и требовалось доказать.

Числа α_k. Пусть х_i<х_i+1 при

Обозначим:

Данные числа обладают следующими свойствами:

1. - очевидно

2. Действительно, т.к.

1)

2) Умножим на (-1)^n-i. Тогда знак числителя не зависит от i, значит знак каждого слагаемого такой же, отсюда, α_i>0.

3.

Действительно:

Из ранее доказанной Леммы:

Что и требовалось доказать.

§8. Задача Чебышева. Разрешимость системы

Пусть f(х) задана дискретно в узлах х₀...х_n+1 значениями у₀...у_n+1 соответственно (х_i<x_i+1). Требуется построить многочлен Р_n(x), наилучшим образом аппроксимирующий в узлах значения функции.

Задача Чебышева.

Обозначим:

Р_n(x)=P_n(x,A), где А=(а₀, а₁...а_n).

Необходимо определить μ=inf max |P_n(x_k)-y_k| и минимизирующий многочлен P_n(x,A), если он существует.

Задачи такого типа называют минимальными.

Предварительно рассмотрим систему:

В системе n+2 неизвестных: h, а₀, а₁...а_n.

Докажем, что определитель системы Δ≠0.

Заметим, что:

а) sgn Δ₀=sgn Δ₁

Действительно, рассмотрим функцию q₀(x):

- многочлен n-ого порядка с нулями

в х₂, х₃...х_n+1

Отсюда, sgn q₀(x₀)=sgn q₀(x₁), т.к. точки промежутку знакопостоянства функции.

б) sgn Δ₁ = sgn Δ₂

Рассмотрим следующую функцию:

- многочлен n-ого порядка с нулями

в х₀, х₃...х_n+1

Отсюда, sgn q₁(x₁)=sgn q₁(x₂). И т.д.

Таким образом, получим: Δ≠0, следовательно, решение системы существует. Обозначим его как P_n(x,A*).