
- •Лекция №1
- •Введение
- •Закон сохранения электрического заряда
- •Взаимодействие точечных зарядов. Закон Кулона
- •Электрическое поле. Напряженность электрического поля.
- •Напряженность поля точечного заряда
- •Линии напряженности.
- •Потенциальная энергия пробного заряда в поле точечного заряда (потенциальная энергия системы двух точечных зарядов). Потенциал электрического поля.
- •Работа по перемещению заряда в электрическом поле. Условие потенциальности электрического поля.
- •Эквипотенциальные поверхности.
- •Вектор градиента потенциала электрического поля. Связь напряженности и градиента потенциала.
- •Графическое изображение электрических полей.
- •Поток вектора напряженности электрического поля.
- •Теорема Гаусса
- •Дивергенция векторного поля
- •Теорема Гаусса в дифференциальном виде
- •Применение теоремы Гаусса для расчёта электрических полей
- •Поле бесконечной, равномерно заряженной плоскости
- •Две бесконечные плоскопараллельные разноименно заряженные плоскости
- •Бесконечный равномерно заряженный цилиндр (нить)
- •Два коаксиальных бесконечных равномерно заряженных цилиндра
- •Заряженная сфера
- •Концентрические равномерно заряженные сферы
- •Поле равномерно заряженного шара Принцип суперпозиции полей
- •Электрический диполь. Электрический (дипольный) момент
- •Поле точечного диполя
- •Энергия диполя в поле
- •Момент сил, действующих на диполь. Сила, действующая на диполь в неоднородном поле.
- •Электрическое поле в диэлектриках
- •Механизмы поляризации
- •Поверхностные и объёмные связанные заряды
- •Электростатическое поле в диэлектрике
- •А следовательно, . Таким образом, физической причиной ослабления поля в диэлектрике является поляризация его и появление собственного поля поляризационных связанных зарядов.
- •Вектор электрической индукции (электрического смещения)
- •Связь между векторами и .
- •Поведение векторов и на границе двух сред
- •Сегнетоэлектрики
- •В зависимости от сегнетоэлектрика петля может быть широкой или узкой.
- •Пьезоэлектрики
- •Проводники в электрическом поле
- •Поле заряженного проводника
- •Электроемкость уединенного проводника. Электроемкость проводящего шара
- •Конденсаторы. Емкость конденсаторов
- •Емкость плоского конденсатора
- •Емкость сферического конденсатора
- •Емкость цилиндрического конденсатора
- •Соединение конденсаторов
- •Энергия системы точечных зарядов
- •Энергия заряженного проводника
- •Энергия конденсатора
- •Энергия электрического поля
- •Законы постоянного тока Электрический ток
- •Плотность тока
- •Сторонние силы. Эдс сторонних сил. Напряжение.
- •Закон Ома для однородного участка цепи. Сопротивление проводника.
- •Закон Ома в дифференциальной форме
- •Закон Джоуля — Ленца
- •Закон Ома для замкнутой цепи. Закон Ома для неоднородного участка цепи
- •Разветвленные цепи. Правила Кирхгофа
- •Работа и мощность тока
- •Электронная теория проводимости металлов (классическая теория Друде — Лоренца)
- •Закон Ома в электронной теории
- •Закон Джоуля — Ленца в электронной теории
- •Закон Видемана — Франца в электронной теории
- •Затруднения классической электронной теории металлов
- •Сверхпроводимость
- •Работа выхода электрона из металла Работа, которую нужно затратить для удаления электрона из твердого тела в вакуум, называется работой выхода.
- •Контактная разность потенциалов
- •Термоэлектрические явления и их применение
- •Явление Зеебека.
- •Явление Пельтье.
- •3.Явление Томсона
- •Термоэлектронная эмиссия
- •Квантовая теория. Энергетические состояния электронов в твердых телах. Энергия Ферми
- •Классификация твердых тел по зонной теории
- •Объяснение затруднений классической теории металлов. Как справилась с затруднениями квантовая теория?
- •Полупроводники Собственная проводимость полупроводника
- •Примесная проводимость полупроводников
- •Полупроводник типа n
- •Полупроводник типа p
- •Объяснение p-n перехода с квантовой точки зрения
Дивергенция векторного поля
Положительные заряды являются источниками электрического поля, (силовые линии поля выходят из этих зарядов). Отрицательные заряды являются стоками электрического поля, (силовые линии входят в отрицательные заряды).
Для характеристики мощности источников
вводится понятие дивергенции
(расходимость), определяемой формулой: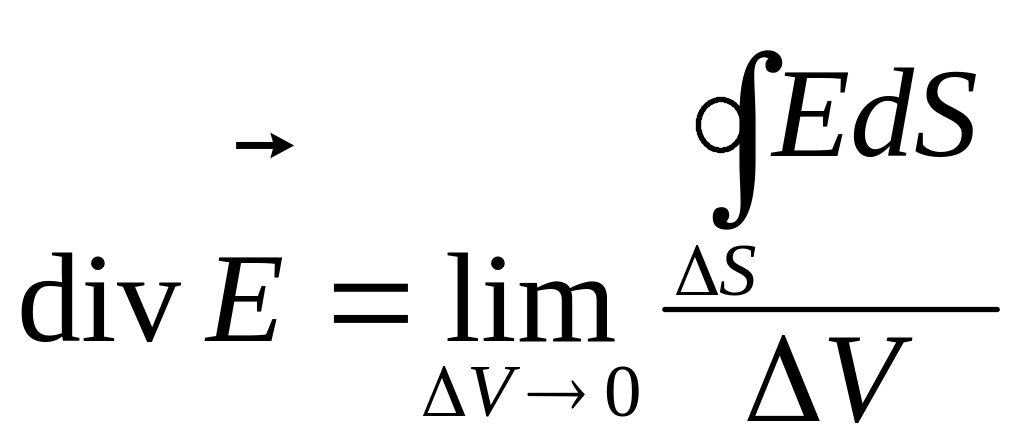 ,
где
,
где
![]() — малая
замкнутая поверхность, ограничивающая
малый объём
— малая
замкнутая поверхность, ограничивающая
малый объём
![]() .
.
Дивергенция соответствует потоку, исходящему из замкнутой поверхности, приходящему на единицу объёма.
Выражение
дивергенции
![]() в
декартовых прямоугольных координатах
имеет вид:
в
декартовых прямоугольных координатах
имеет вид:
![]() ,(доказывается
в математике). Используя,
векторно-дифференциальный оператор
«набла», (
)
запишем дивергенцию, как скалярное
произведение векторов
,(доказывается
в математике). Используя,
векторно-дифференциальный оператор
«набла», (
)
запишем дивергенцию, как скалярное
произведение векторов
![]() и
:
и
:
![]()
Теорема Гаусса в дифференциальном виде
Из определения дивергенции для малой
замкнутой поверхности
![]() справедливо:
справедливо:![]() .
Для всех точек внутри этой поверхности
.
Для всех точек внутри этой поверхности
![]() .
.
Для замкнутой поверхности S
больших размеров это равенство будет
выполняться в интегральном виде
![]() ,
(2)
,
(2)
где V — объём, ограниченный замкнутой поверхностью S. Приведённое равенство доказывается в математике и имеет название «теорема Остроградского-Гаусса».
Применив теоремы Гаусса (1) и Остроградского-Гаусса (2) видим, что левые части этих равенств одинаковы, а, следовательно, будут равны и правые части:
![]() .
Это соотношение справедливо при любом
объёме V, тогда будет
справедливым равенство
.
Это соотношение справедливо при любом
объёме V, тогда будет
справедливым равенство
![]() ,
называемое дифференциальной формулировкой
теоремы Гаусса. Выражая дивергенцию
через оператор «набла» запишем,
,
называемое дифференциальной формулировкой
теоремы Гаусса. Выражая дивергенцию
через оператор «набла» запишем,
![]() .
.
Применение теоремы Гаусса для расчёта электрических полей
В некоторых случаях применение теоремы Гаусса облегчает задачу расчета электрических полей, по сравнению с интегрированием проведённым по принципу суперпозиции полей. Расчет с применением теоремы Гаусса проводят по следующей схеме:
Необходимо выяснить, исходя из соображений симметрии, направление силовых линий и геометрическую форму эквипотенциальных поверхностей.
Провести такую, воображаемую замкнутую поверхность через данную точку поля, чтобы поток напряжённости электрического поля через эту поверхность нашёлся наиболее легко (практически устно). Приравняв его к заряду, находящемуся в объёме этой поверхности (делённому на электрическую постоянную) составим уравнение, из которого найдем напряженность электрического поля E.
Поле бесконечной, равномерно заряженной плоскости
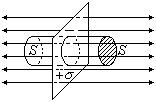
![]() .
По теореме Гаусса этот же поток
определяется зарядом той части плоскости,
которая лежит внутри цилиндра, и равен
.
По теореме Гаусса этот же поток
определяется зарядом той части плоскости,
которая лежит внутри цилиндра, и равен
![]() .
Сравнивая эти выражения для потока
.
Сравнивая эти выражения для потока
![]() ,
находим
,
находим
![]() .
.
Для равномерно заряженной пластины конечных размеров полученное выражение приближенно справедливо в области, находящейся достаточно далеко от краев пластины и не слишком далеко от ее поверхности.
