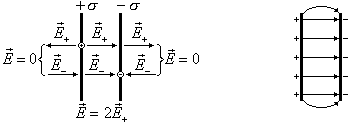
Две бесконечные плоскопараллельные разноименно заряженные плоскости

Пусть плоскости заряжены равномерно разноименными зарядами с поверхностными плотностями , и . Поле таких плоскостей найдем как суперпозицию полей, создаваемых каждой из плоскостей в отдельности, , где и — поля, создаваемые положительно и отрицательно заряженными плоскостями. Как видно из рисунка напряженности, создаваемые обеими плоскостями правее правой и левее левой плоскостей, направлены в противоположные стороны, и при суммировании взаимно компенсируют друг друга. В этих областях результирующее поле равно нулю, .

Напряженности полей обеих плоскостей между плоскостями направлены в одну сторону, следовательно, модуль напряженности результирующего поля равен сумме модулей напряженностей, накладываемых полей. Напряженность поля каждой плоскости равна , тогда полная напряженность между плоскостями , т. е.

Поле, как и в случае одной пластины будет однородным. Полученный результат приближенно справедлив и для плоскостей конечных размеров, если линейные размеры пластин много больше расстояния между ними. Такая система образует плоский конденсатор. Картина поля плоского конденсатора приведена на рисунке. Поле получается однородным всюду, кроме областей вблизи краев пластины. В дальнейшем при расчетах краевыми эффектами будем пренебрегать, и считать поле плоского конденсатора однородным.

Бесконечный равномерно заряженный цилиндр (нить)

Возьмем цилиндрическую поверхность радиуса R, заряженную с постоянной линейной плотностью (заряд приходящийся на единицу длинны вдоль оси цилиндра). Из соображений симметрии следует, что поле здесь имеет радиальный характер, т. е. вектор в каждой точке перпендикулярен оси цилиндра, а модуль вектора зависит только от расстояния до оси цилиндра. В качестве замкнутой поверхности применения теоремы Гаусса выберем поверхность коаксиального, прямого цилиндра (смотрим рисунок). Тогда поток вектора сквозь торцы этого цилиндра равен нулю, и полный поток через замкнутую поверхность равен потоку через боковую поверхность , где — площадь боковой поверхности, выбранного цилиндра, — его длинна.

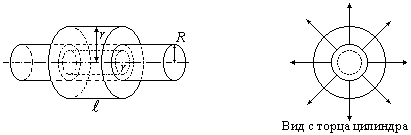
По теореме Гаусса для случая этот же поток определяется зарядом, вырезаемый выбранной замкнутой, цилиндрической поверхностью на заряженном цилиндре (длинною ), и равен . Сравнивая эти выражения для потока , находим

.

Если , то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области . Внутри равномерно заряженного цилиндра поля нет.

Два коаксиальных бесконечных равномерно заряженных цилиндра

Воспользуемся предыдущим результатом и принципом суперпозиции. Между цилиндрами поле определяется выражением , так как в этой области поле, создаваемое внешним цилиндром, равно нулю. Вне большого цилиндра вектора и направлены в разные стороны, и результирующее поле . Два таких проводящих цилиндра представляют собой цилиндрический конденсатор. Картина поля такого конденсатора показана на рисунке.

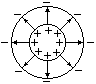
Заряженная сфера

Пусть q — заряд, равномерно распределенный на сфере радиуса R. Очевидно, из соображений симметрии направление вектора в любой точке проходит через центр сферы, а модуль вектора должен зависеть только от расстояния r до центра сферы. Такое поле является центрально-симметричным, силовые линии идут радиально от поверхности сферы. В качестве замкнутой поверхности надо взять концентрическую сферу. Пусть ее радиус , тогда по теореме Гаусса , откуда

.

Вне заряженной поверхности поле убывает с расстоянием r по такому же закону, как у точечного заряда.

Если , то замкнутая поверхность не содержит внутри зарядов, поэтому в этой области всюду , т. е. внутри равномерно заряженной сферической поверхности электрическое поле отсутствует.