5. Тем волна (параметры)

Поперечными электромагнитными волнами принято называть волны для которых характерно отсутствие продольных составляющих как электрического , так и магнитного

векторов, сокращенно называют ТЕМ.

Простейшим примером волны типа ТЕМ может служить переменное электромагнитное поле, образующееся в волноводе из двух проводящих плоскостей при распространении плоской электромагнитной волны, имеющей параллельную поляризацию и падающей под углом φ=90⁰как показано на рисунке.

Данное поле по своей конфигурации полностью совпадает с однородной плоской

волной; роль идеально проводящих стенок сводится лишь к локализации поля в пространстве.

Основные свойства волн типа ТЕМ:

1)Поскольку граничные условия для вектора Е в изображенной линии передачи удовлетворяется автоматически, структура поля не зависит от расстояния между плоскостями и от длины волны.

(λ_кр)_ТЕМ=∞

то есть система пропускает колебания всех частот вплоть до постоянного тока.

2)Механизм распространения волны типа ТЕМ не связан с явлениями многократных отражений от стенок. Поэтому

(λ_в)_ТЕМ=λ₀

Здесь λ₀ следует понимать длину однородной плоской волны в заполняющем диэлектрике.

3)Характеристическое сопротивление волны типа ТЕМ, обозначенное как Z_сТЕМ и равное отношению амплитуды элек. поля к амплитуде маг.поля, совпадает с аналогичной величиной ,вычисленной для однородной плоской волны в неограниченном пространстве.

Действительно,

Z_сТЕМ= limZ_cE= limZ_cH=Z_c

λ_кр→∞ λ_кр→∞

7. Дивергенция вектора. Пребразования Остроградского-Гауса

Дивергенция вектора D-это лимит

-поток вектора D через замкнутую поверхность S

∆V→0

DdS=DdS(cos(D)Ds)

Направление вращения определяется по правилу буравчика

Поле определенно или известно значение D в каждой точке

Дивергенция вектора D-это расхождение данного вектора в какой-то

∆V→0 точке.

Векторное преобразование Остроградского-Гаусса это есть переход от двойного интеграла(интеграла по поверхности) к тройному интегралу(интегралу по объёму).

Это преобразование применяется что бы перейти от дифференциальной формы закона Гаусса divD= =ρ к интегральной

Разобьём рассматриваемый объём на бесконечно малые параллелепипеды с объёмом dV и поверхностью dS.

Элементарный поток вектора D через объём

Суммарный общий поток через поверхность S будет равен сумме потоков через элементарные поверхности dS.

Поскольку между гранями разбитых ячеек с одной стороны поток входит с одним знаком, а с другой стороны выходит с противоположным знаком ,то все такие потоки между соседними гранями внутри поверхности S сократятся

преобразование Остроградского

8. Дивергенция вектора в прямоугольной системе координат.

Найдём значение дивергенции в прямоугольной системе координат

Окружаем точку поверхностью в виде параллелепипеда

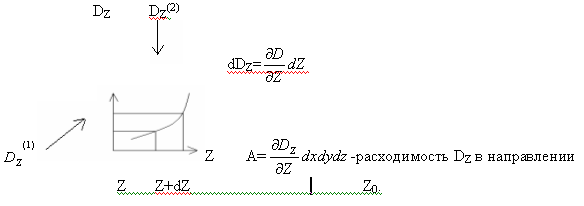
Общий поток через поверхность dS с объёмом dV=dx*dy*dz

Z.Входная грань-1,выходная-2

X 3,4

Y 5,6

Поток вектора в направлении Z равен разности выходного потока из поверхности 2 и входным потоком поверхности 1 площадью dxdy

-расходимость вектора в направлении X₀

- расходимость вектора в направленииY₀

По определению

div

Расходимость проэкции dD_Z в направлении Z₀ равняется чувствительности к изменению величины dZ на единицу длины в направлении Z и умножить на величину dZ(на перпендикулярную грань dX-dY по направлению к Z)

8 продолжение

-вектор чувствительности,

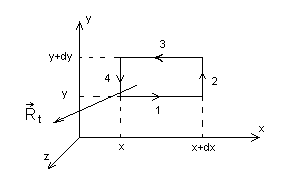
9. Ротор вектора. Теорема Стокса.

Теорема Стокса (преобразования)

Е сли суммировать циркуляции вектора H к определенным бесконечно малым контурам, то на смежных линиях циркуляции с противоположным знаком сложатся и в сумме останется циркуляция по наружному контуру L.

Ротор вектора

∆S→0

В отличии от операции ”div” ротор вектора –это вектор циркуляции H по замкнутому контуру dl- это

10. Ротор вектора в прямоугольной системе

координат.

11. закон Гаусса в дифференциальной и интегральной формах. Переход

Этот закон получен экспериментально и устанавливает связь между векторным полем Е и вели­чиной порождающего его заряда. Рас­смотрим некоторый объем V, ограниченный замкнутой поверхностью S (рис), если внутри объема V за­ключен суммарный электри­ческий заряд, то его ве­личина, деленная на элек­трическую постоянную ва­куума ε₀, численно совпадает с потоком векторного по­ля Е через поверхность S. Математически закон Гаусса в вакууме записывается как

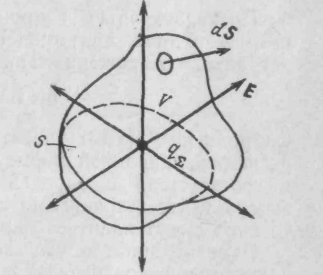
Если рассматриваются точечные заряды, то величина q, может быть найдена алгебраическим суммированием. Если же заряд распределен непрерывно, то Q. определя­ется интегрированием плотности заряда р по объему V:

Закон Гаусса, выражаемый формулой, связы­вает поток вектора электрического поля с суммарным зарядом, заключенным внутри объема. Поэтому данная формулировка носит название закона Гаусса в инте­гральной форме. Пользуясь методами векторного ана­лиза, можно получить другую форму записи данного закона.

Поскольку объем V произволен, последнее равенство возможно лишь при тождественном совпадении подын­тегральных выражений. Таким образом,

Соотношение (1.13) носит название закона Гаусса в дифференциальной форме. Физически это соотношение в соответствии с определением понятия дивергенции означает, что источниками силовых линий электрическо­го поля могут являться лишь электрические заряды.