22. Закон непрерывности зарядов.

Одно из основных положений теории электромагне­тизма состоит в том, что ни при каких условиях электри­ческие заряды не могут ни самопроизвольно зарождать­ся, ни исчезать бесследно. Это положение многократно подтверждается экспериментами и является одним из фундаментальных физических законов — законом сохранения заряда.

Предположим, что внутри произвольного замкнутого объема V с поверхностью S содержится некоторый за­ряд Q, величина которого может быть найдена интегри­рованием плотности заряда р по всему объему:

Если теперь предположить, что с течением времени ве­личина Q по каким-либо причинам изменяется, то в со­ответствии с законом сохранения заряда следует счи­тать, что часть зарядов пересекает поверхность S, вызы­вая наличие тока проводимости с плотностью J_np.

Интегрируя J_пр поверхности 5, получаем резуль­тирующий ток проводимости

По определению

(ток считается положительным, если заряд внутри объема уменьшается). Отсюда с учетом предыдущих формул будем иметь

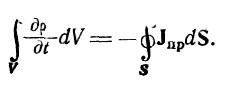
Преобразовав правую часть по теореме Остроградско­го — Гаусса, получим

Последнее тождество из-за полной произвольности объема V возможно лишь при тождественном совпаде­нии подынтегральных выражений.

В результате приходим к математической формули­ровке закона сохранения заряда, носящей название уравнения непрерывности:

23. Уравнение Максвелла для гармонических колебаний. Комплексная диэлектрическая проницаемость

Если воспользоваться материальным уравнением, то первое уравнение Максвелла может быть записано в виде

где носит название комплексной ди­электрической проницаемости данного веще­ства.

Введение комплексной диэлектрической проницаемо­сти позволяет весьма просто учитывать как диэлектри­ческие, так и проводящие свойства данного вещества. Значение вещественной ча­сти говорит об интенсив­ности процесса поляризации, в то время как мнимая часть характеризует плотность то­ков проводимости. Изобра­жая число «_а на комплексной плоскости (рис. 1.13), мож­но характеризовать соотношение между веществен­ной и мнимой частями при помощи угла б, носящего на­звание угла диэлектрических потерь. Чем больше этот угол, тем относительно большая часть элек­тромагнитной энергии рассеивается в виде тепла при протекании токов проводимости. На практике чаще все­го пользуются тангенсом этого угла:

Тангенс угла потерь хороших диэлектриков на СВЧ ле­жит в пределах 10^-4-10^-3; если tg »10-³, то диэлек­трик обычно считается плохим

24.Уравнение Гельмгольмца для плоской эм волны в однородном диэлектрике

В физике колебательное движение непрерывной среды принято называть волновым процессом

Можно доказать волновой характер эл. поля математически ,сводя уравнения Максвелла к другим уравнениям ,которые описывают волновой процесс.

Рассмотрим эл. поле в некоторой области пространства ,где плотность зарядов отсутствует т.е. ρ=0.

Плотность сторонних эл.токов также равна 0.

Выпишем два уравнения

Применим операцию rot к левой и правой частям второго уравнения, а затем выразим полученную правую часть первое уравнение

Здесь в общем случае комплексное число, являющееся постоянной распространения электромагнитной волны. Для величины γ можно встретить также названия фазовая постоянная или волновое число.

Дальнейшее преобразование формулы можно осуществить, если воспользоваться известным тождест­вом векторного анализа:

Здесь ² (читается „набла квадрат") — векторный диф­ференциальный оператор второго порядка, конкретная форма которого полностью определяется той координат­ной системой, в которой проводятся вычисления. В де­картовой координатной системе действие оператора ² сводится к тому, что к каждой из проекций векторного поля применяется оператор Лапласа

Если воспользоваться законом Гаусса, который в со­ответствии с принятым условием ρ=0 обеспечивает div E’= 0, то уравнение может быть записано в следующем виде:

Пользуясь симметрией уравнений Максвелла, совер­шенно аналогично получаем также уравнение относи­тельно векторного поля Н:

Предыдущие 2-а уравнения носят название уравнений Гельмгольца по име­ни выдающегося немецкого физика Г. Гельмгольца. Можно показать, что эти уравнения опи­сывают стационарные волновые процессы, т. е. распро­странение в пространстве волн с некоторой постоянной частотой.

В координатной форме уравнение Гельмгольца записывается следующим образом:

или

25 Плоские волны. Рассмотрим безграничное трехмерное пространство с декартовой системой координат х, у,z ,в каждой точке которого задана некоторая величина А (физическая природа ее безразлична), которая во време­ни и в пространстве меняется по закону

При этом говорят, что в пространстве существует монохроматическая плоская волна. Аргумент косинуса, т. е ωt±βz,называемый обычно фазой волны, является функцией времени t и пространственной координаты z.

Если зафиксировать г, то величина А принимает те же самые значения через промежутки времени, кратные пе­риоду T=2π/ω. Если же фиксировано время, то величи­на А изменяется периодически вдоль оси Z с периодом λ , называемым длиной волны. Легко видеть, что величи­ны λ и β связаны друг с другом:

Число β служит важнейшей характеристикой волнового процесса и носит название постоянной распро­странения волны. Употребляются также термины фазовая постоянная и волновое число. Физиче­ский смысл величины β состоит в том, что она указывает, на сколько радиан изменяется фаза волны при прохож­дении одного метра пути.

Наличие двух возможных знаков в формуле связано с тем, что плоские волны могут распространять­ся в двух противоположных направлениях. Назовем по­верхность, удовлетворяющую уравнению

волновым фронтом плоской волны Очевидно, что в рассматриваемом случае волновые фронты представля­ют собой бесконечные плоскости, перпендикулярные оси г и перемещающиеся в пространстве со скоростью

носящей название фазовой скорости.