4.2 Решение задач нелинейного программирования с ограничениями-равенствами

Основными среди точных методов решения задач нелинейного программирования данного типа является метод множителей Лагранжа.

Теорема. Если - точка локального минимума дифференцируемой функции , то при ограничениях , удовлетворяющих некоторому условию регулярности, для функции Лагранжа

(4.3.)

существует вектор множителей Лагранжа такой, что

, (4.4)

. (4.5.)

Замечания. 1.Множители Лагранжа имеют произвольные знаки.

2. Если f и выпуклы, то необходимые условия (4.4.), (4.5.) являются и достаточными для существования решения задачи (4.1.), (4.2.).

3. Требование регулярности связано с существованием решения системы (4.4.), (4.5.).

Метод множителей Лагранжа позволяет отыскивать максимум или минимум функции при ограничениях–равенствах, т.е. в (4.1) все ограничения являются равенствами. Основная идея метода заключается в переходе от задачи на условный экстремум к задаче отыскания безусловного экстремума некоторой специально построенной функции Лагранжа.

Пусть требуется найти

(4.6.)

при ограничениях

(4.7.)

Составим функцию Лагранжа следующего вида:

Для того чтобы вектор являлся решением задачи (4.6.), (4.7.) , необходимо существование такого вектора , чтобы пара векторов удовлетворяла системе уравнений:

Пример 11. В двух цехах предприятия нужно изготовить 20 изделий некоторой продукции. Затраты, связанные с изготовлением х₁ изделий в 1-м цехе, равны руб., а затраты при изготовлении х₂ изделий во 2-м цехе равны руб. Составить план производства изделий в двух цехах с минимальными затратами.

Решение. Математическая модель задачи:

Запишем функцию Лагранжа

Для данной точки получим в точке экстремума:

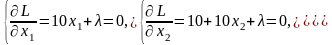
Исследуем характер функции f в окрестности точки , для этого находим

Так как и , то функция выпукла, и точка - точка минимума.

Ответ: Оптимальный план изделий.

4.3. Решение задач нелинейного программирования с ограничениями-неравенствами

Имеется задача нелинейного программирования с ограничениями-неравенствами:

(4.8)

при условиях

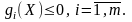(4.9)

Допустим, что функции и все , выпуклы по Х. Такая задача носит название выпуклого программирования и множество решений , определяемое условиями (4.9), является выпуклым. Для задачи (4.8), (4.9) справедлива теорема Куна-Таккера.

Теорема. Пусть , , обладают непрерывными частными производными на некотором открытом множестве пространства , содержащем . Если является точкой минимума при ограничениях , удовлетворяющих некоторому дополнительному условию регулярности, то существуют такие неотрицательные множители Лагранжа для которых выполняются следующие условия:

(4.10)

(4.11)

Последнее условие называется условием дополняющей нежесткости.

Если функции и - выпуклы по Х, то условия оптимальности (4.10), (4.11) будут не только необходимыми, но и достаточными. В этом случае условие существования решения Х и , удовлетворяющего (4.10), (4.11), которое называют условием регулярности, примет вид

для всех .

Пользуясь теоремой Куна-Таккера, задачу нелинейного программирования решают следующим образом.

Шаг 1. Составляют функцию Лагранжа

Шаг 2. Составляют систему уравнений вида (4.10), (4.11).

Шаг 3. Находят ее решение . В отличие от задачи с ограничениями-равенствами вектор должен в этом случае удовлетворять условию неотрицательности.

Часто в задачах исследования операций приходится решать задачи, в которых переменные , должны удовлетворять условию .

Основные положения теории могут быть легко распространены на этот случай. Тогда к ограничению (4.9) следует добавить следующее ограничение:

(4.12)

Это ограничение в общем виде можно записать как

.

Задача представлена в каноническом виде. Применим к ней теорему Куна-Таккера, для чего составим функцию Лагранжа

(4.13)

где - множители, связанные с ограничениями (4.12). Условия теоремы Куна-Таккера выглядят так:

Последнее соотношение представляет собой условия дополняющей нежесткости для ограничений неотрицательности.

Теорема. Пусть задача нелинейного программирования имеет вид

при условиях:

,

а функции и дифференцируемы и выпуклы по Х. Вектор является оптимальным решением задачи тогда и только тогда, когда существует такой вектор , что пара является седловой точкой функции Лагранжа , т.е. выполняются следующие условия:

Пример 12. Предприятие выпускает два вида изделий А и Б. Норма расхода на производство каждого вида изделий приведены в таблице. При этом известно, что сырья имеется 12 т, а оборудования - 30 станко-часов.

Ресурсы	Норма расхода ресурсов на 1 изделие		Запас ресурсов
	Изделие А	Изделие Б
Сырье, т	3	2	12
Оборудование, станко-час	5	6	30
Оптовые цены, руб.	9	7

Определить оптимальный план реализации продукции, если себестоимость одного изделия соответственно равна руб. и руб., где и - план выпуска изделий вида А и Б.

Решение.

Математическая запись задачи. Прибыль предприятия при плане равна

.

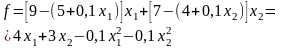Для удобства решения перейдем от задачи , к задаче . Тогда ее модель получит вид

Функция Лагранжа получит вид

.

Для данной функции в точке экстремума получим:

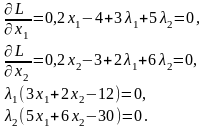
При решении данной системы уравнений рассмотрим четыре случая.

1. Этот случай соответствует предположению о том, что - внутренняя точка Х. Тогда

Откуда

Но эта точка не принадлежит Х, так как условие (4.9) не выполняется, т.е.

2. Из и условия (4.8) следует, что точка лежит на границе . Получаем систему линейных уравнений вида

Решив данную систему уравнений, получаем

3. Случай невозможен.

4. Случай невозможен.

Ответ. Оптимальный план изделий.