2.3. Решение матичной игры в смешанных стратегиях

Если платежная матрица не имеет седловой точки, т.е. и , то применение чистых стратегий не дает оптимального решения игры. В этом случае можно получить оптимальное решение, случайным образом чередуя (выбирая) чистые стратегии, т.е. используют смешанную стратегию.

Смешанной стратегией игрока А называется применение чистых стратегий с вероятностями , причем: .

Смешанные стратегии игрока А записываются в виде матрицы или в виде строки .

Аналогично смешанные стратегии игрока В обозначаются: или в виде строки , где .

Пример 5. Найти верхнюю и нижнюю цену, заданной платежной матрицей

.

Решение. Платёжная матрица, в которой не существует решения в чистых стратегиях

.

Так как нижняя цена игры достигается в стратегии А₁ и её значение равно 2, в то время как верхняя цена игры достигается в стратегии В₄ и её значение равно 3.

Теорема Неймана. Каждая конечная игра имеет, по крайней мере, одно оптимальное решение в области смешанных стратегий.

Обозначим 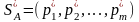и - пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Теорема об активных стратегиях: если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры , если второй игрок не выходит за пределы своих активных стратегий.

Если в платежной матрице все элементы i-й строки не меньше соответствующих элементов к-й строки, то i-я стратегия игрока А называется доминирующей над к-й стратегий, а к-я – доминируемой. Если все элементы j-го столбца платежной матрицы не больше соответствующих элементов к-го столбца, то j-я стратегия игрока В называется доминирующей над к-й стратегией.

Первому игроку невыгодно применять стратегии, которым соответствуют доминируемые строки; второму игроку невыгодно применять стратегии, которым соответствуют доминирующие столбцы. Поэтому при решении игры можно уменьшить размеры платежной матрицы путем удаления из нее доминирующих столбцов и доминируемых строк.

Пример 6. Определите, имеет ли платёжная матрица

доминируемые и доминирующие стратегии.

Решение.

Рассмотрим платежную матрицу

,

Все элементы стратегий А₂ и А₄ меньше элементов стратегии А₃. Данные стратегии не будут выбраны игроком, так как являются заведомо проигрышными и удаление этих стратегий из платёжной матрицы не повлияет на определение нижней и верхней цены игры, описанной данной матрицей. Исключим стратегии А₂ и А₄.

.

Для второго игрока. Все элементы стратегий В₁, В₂ и В₃ больше элементов стратегии В_4, поэтому их можно исключить. В результате преобразований получим матрицу

,

2.4. Игра 2 2

Рассмотрим игру 2 2, которая является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке.

В игре, где отсутствует седловая точка, в соответствии с основной теоремой теории игр оптимальное решение существует и определяется парой смешанных стратегий и .

Игра задана платежной матрицей .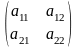

Средний выигрыш игрока А, если он использует оптимальную смешанную стратегию , а игрок В – чистую стратегию В₁ (это соответствует 1-му столбцу платежной матрицы P), равен цене игры , т.е. . Тот же средний выигрыш получает игрок А, если игрок В применяет стратегию В₂, т.е. . Учитывая, что , получаем систему уравнений для определения оптимальной стратегии и цены игры :

Решая эту систему, получим оптимальную стратегию :

,

,

и цену игры .

Применяя теорему об активных стратегиях при отыскании - оптимальные стратегии игрока В определяются по формулам:

,

.

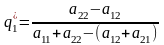Решение игры 2 2 приведенной выше платежной матрицы допускают наглядную геометрическую интерпретацию. По оси абсцисс (рис. 1) надо отложить единичный отрезок А₁А₂; точка А₁ (x=0) изображает стратегию А₁, а все промежуточные точки этого отрезка – смешанные стратегии S_A первого игрока, причем расстояние от S_A до правого конца отрезка – это вероятность стратегии А₁, расстояние до левого – вероятность стратегии А₂. На перпендикулярных осях I-I и II-II откладываем выигрыши при стратегиях А₁ и А₂ соответственно. Если 2-й игрок примет стратегию В₁, то она дает выигрыши и на осях I-I и II-II, соответствующие стратегиям А₁ и А₂. Обозначим эти точки на осях I-I и II-II буквой В₁. Средний выигрыш , соответствующий смешанной стратегии S_A, определяется по формуле математического ожидания и равен ординате точки М₁, которая лежит на отрезке В₁В₁ и имеет абсциссу S_A (рис. 1).

Аналогично строим отрезок В₂В₂, соответствующий применению вторым игроком стратегии В₂ (рис 2). При этом средний выигрыш - ордината точки М₂.

I

II

B₁

y

II

M₁

a₂₁

В₁

B₂

a₁₁

a₂₂

P₂

P₁

x

x

А₁

А₂

A₂

I

II

II

Рис. 1

I

y

II

M₂

B₂

a₁₂

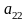
A₁

P₂

P₁

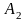
I

Рис. 2

II

В соответствии с принципом минимакса оптимальная стратегия такова, что минимальный выигрыш игрока А (при наихудшем поведении игрока В) обращается в максимум. Ординаты точек, лежащих на ломаной (рис. 3), показывают минимальный выигрыш игрока А при использовании им любой смешанной стратегии (на участке В₁N – против стратегии В₁, на участке NВ₂ – против стратегии В₂). Оптимальную стратегию определяет точка N, в которой минимальный выигрыш достигает максимума; ее ордината равна цене игры . На рис. 3 обозначены верхняя и нижняя цены игры и .

Пример 7. Дайте геометрическую интерпретацию решения игры для двух игроков. Для проверки геометрического решения проведите также алгебраические расчеты и сравните результаты с полученными геометрическим способом для платежной матрицы .

Решение. Игра не имеет седловой точки, так как Оптимальное решение следует искать в смешанных стратегиях.

Геометрическая интерпретация игры . Построим на плоскости отрезки, соответствующие стратегиям второго игрока. Найдем оптимальную стратегию игрока А. Откладываем по оси абсцисс единичный отрезок А₁А₂;

точка А₁(х=0) изображает стратегию А₁, а все промежуточные точки отрезка А₁А₂ – смешанные стратегии S_A первого игрока, причем расстояние от S_A до правого конца отрезка – это вероятность p₁ стратегии А₁, расстояние до левого конца - вероятность p₂ стратегии А₂. На осях Y и Y¹ откладываем выигрыши при стратегиях А₁ и А₂ соответственно. На вертикальной оси Y откладываем отрезки , соответствующий стратегии В₁, , соответствующий В₂. На вертикальной оси Y¹ откладываем отрезки , соответствующий стратегии , , соответствующий . Абсцисса точки N определяет стратегию S_A , ордината – цену игры . Точка N является точкой пересечения прямых и . 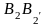Уравнения прямой , проходящей через точки (0,1), (1,2): или .Уравнение прямой , проходящей через точки (0,3), (1,1): или . Точка пересечения прямых является решением системы

Точка N . Тогда . Оптимальная стратегия S_A = . Цена игры .

Геометрически можно так же определить оптимальную стратегию игрока В, если поменять местами игроков А и В. Абсцисса точки М определяет q₂

в оптимальной стратегии игрока В, ордината этой точки – цена игры. Прямая , проходящая через точки (0,1), (1,3), удовлетворяет уравнению . Прямая , проходящая через точки (0,2), (1,1), удовлетворяет уравнению . Координаты их точки пересечения М:

Откуда . Оптимальная стратегия S_в= .

Алгебраические расчеты игры . Оптимальная стратегия определяется по формуле:

,

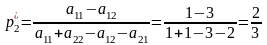
и цену игры

.

Оптимальная стратегия определяется по формуле:

,

.

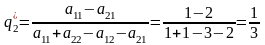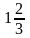Ответ: Оптимальные смешанные стратегии игроков , цена игры составляет . Если первый игрок с вероятностью 1/3 будет применять первую стратегию и с вероятностью 2/3 вторую, то при достаточно большом количестве игр с данной матрицей его выигрыш в среднем составит не менее . Если второй игрок с вероятностью 2/3 будет применять первую стратегию и с вероятностью 1/3 вторую, то при достаточно большом количестве игр с данной матрицей его проигрыш в средней составит не более .