Метод Гомори
Основная идея решения целочисленных задач заключается в том, что задача сначала решается без ограничения целочисленности. Если решение получается целочисленным, то задача решена, если нет, то к задаче присоединяют новое дополнительное ограничение, которое называется сечением. Оно обладает следующими:
- оно должно быть линейным;
- должно отсекать найденный оптимальный нецелочисленный план;
- не должно отсекать ни одного целочисленного плана.
Вновь полученную задачу решают методом линейного программирования. Процесс построения сечения и решения задачи повторяется до получения целочисленного оптимального решения. Общий систематический способ построения сечения разработал Гомори в 1958г.
Алгоритм метода Гомори
Пусть дана целочисленная задача линейного программирования: найти максимальное значение функции
при ограничениях
Отбросив условие целочисленности, решаем исходную задачу симплексным методом. Если получится целочисленное оптимальное решение, то задача решена. Если в оптимальном решении не все переменные целочисленны, то строим сечение.
Пусть в оптимальном решении переменная
- дробное число, т.е.
.
Рассмотрим уравнение, в котором
- базисная переменная.
(1.3)
где J – множество индексов свободных переменных.
Разобьем все коэффициенты и свободный член (1.3) на два слагаемых: целую и дробную часть. Целой частью числа а называется наибольшее целое число, не превышающее а. Дробной частью числа а называется разность между число а и его целой частью. Целую часть числа обозначим [a], а дробную часть – {a}, т.е. а=[a]+{a}. Тогда уравнение (1.3) примет вид
(1.4)
или
.
Для любого целочисленного решения задачи левая часть уравнении (1.4) есть целое число, следовательно, правая часть также будет целым числом.
Неравенство
(1.5)
является сечением Гомори.
Покажем, что любое целочисленное решение
задачи удовлетворяет этому неравенству,
а нецелочисленное решение ему не
удовлетворяет. Пусть
- целочисленное решение, и предположим,
что оно не удовлетворяет неравенству
(1.5), т.е.
,
или
по условию
,
,
отсюда
,
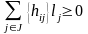кроме того,
.
Получим
,
или
,
т.е.является дробным числом.
Подставив
в уравнение (1.4), получим
.
Правая часть уравнения – дробное число, а левая часть – целое число. Получили противоречие. Следовательно, любое целочисленное решение задачи удовлетворяет неравенству (1.5).
Покажем. Что нецелочисленное оптимальное решение не удовлетворяет неравенству (1.5).
Пусть
- нецелочисленное оптимальное решение
задачи. Подставим его в неравенство
(1.5):
,
но
.
Следовательно,
не удовлетворяет неравенств (1.5).
Присоединяя неравенство (1.5) к ранее решенной задаче, получим новую задачу линейного программирования, которую вновь решаем симплексным методом; если ее оптимальное решение окажется целочисленным, то оно и будет оптимальным решением исходной задачи. Если снова получится нецелочисленное решение, то строим новое сечение, и т.д.
Замечание. Если в оптимальном решение несколько переменных нецелочисленные, то сечение строят по базисной переменной, имеющей наибольшую дробную часть.
Если в процессе решения появится уравнение (выражающее основную переменную через не основные) с нецелым свободным членом и целыми остальными коэффициентами, то соответствующее уравнение не имеет решения в целых числах. В этом случае и данная задача не имеет целочисленного оптимального решения.
Недостатком метода Гомори является требование целочисленности для всех переменных – как основных (выражающих, например, в задаче об использовании ресурсов единицы продукции), так и дополнительных переменных (выражающих величину неиспользованных ресурсов, которые могут быть и дробными).
Пример
1. Методом Гомори найти наибольшее
значение функции
при ограничениях
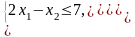
Решение: Решим задачу симплексным методом без учета целочисленности, для этого приведем ее к каноническому виду
-
№
Б.п.
2
2
0
0
1
2
0
0
x3
x4
2
-1
-1
2
1
0
0
1
7
3
-2
-2
0
0
0
1
2
2
0
x1
x4
1
0
-1/2
3/2
1/2
1/2
0
1
7/2
13/2
0
-3
1
0
7
1
2
2
2
x1
x2
1
0
0
1
2/3
1/3
1/3
2/3
17/3
13/3
0
0
2
2
20
Решение нецелочисленное, поэтому строим
сечение Гомори. Возьмем первое уравнение
из последней симплексной таблицы, так
как у х1 наибольшая дробная
часть
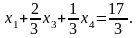
Сечение примет вид
или
.
Присоединив это дополнительное ограничение к ограничениям последней симплексной таблицы, получим новую задачу:
Решим эту задачу симплексным методом.
-
№
Б.п.
2
2
0
0
0
1
2
3
2
2
х1
х2
1
0
0
0
1
0
2/3
1/3
2/3
1/3
2/3
1/3
0
0
-1
7/3
13/3
2/3
1
2
3
2
2
0
x1
x2
x3
1
0
0
0
1
0
0
0
1
0
1/2
1/2
1
1/2
-3/2
5
4
1
0
0
0
1
3
18
Это решение целочисленное, значит
исходная задача решена
.