- •Математическое программирование.
- •Введение
- •1. Целочисленное программирование
- •Метод Гомори
- •Метод ветвей и границ
- •1.3 Задачи для самостоятельной работы
- •2. Теория игр
- •2.1. Основные положения теории игр
- •2.2. Решение матричной игры в чистых стратегиях
- •2.3. Решение матичной игры в смешанных стратегиях
- •2.4. Игра 2 2
- •2.5. Сведение матричной игры к задаче линейного программирования
- •2.6. Игры с природой
- •2.7. Задачи для самостоятельной работы
- •3. Линейный межотраслевой баланс
- •3.2. Задачи для самостоятельной работы
- •4. Нелинейное программирование
- •4.1 Постановка задача нелинейного программирования
- •4.2 Решение задач нелинейного программирования с ограничениями-равенствами
- •4.3. Решение задач нелинейного программирования с ограничениями-неравенствами
- •4.4. Задачи для самостоятельной работы
- •5. Динамическое программирование
- •Долл., долл.,
- •5.3 Задачи для самостоятельной работы
- •6. Контрольные задания
- •Литература
- •Содержание
- •Математическое программирование
4.4. Задачи для самостоятельной работы
1. Определить методом множителей Лагранжа условные экстремумы функций:
1)
 при условии
при условии
 ,
,
2)
 при условии
при условии
 .
.
2. Найти оптимальный набор продуктов
 ,
максимизирующий функцию полезности
,
максимизирующий функцию полезности
 при заданных ценах
и
продуктов
и
и доходе М.
при заданных ценах
и
продуктов
и
и доходе М.
3. Предприятие выпускает изделия двух
видов А1 и А2,
при изготовлении которых используется
сырье I и II.
Известны запасы сырья
 ,
нормы его расхода на единицу изделия
,
нормы его расхода на единицу изделия
 ,
оптовые цены
,
оптовые цены
 за единицу изделия и себестоимость
за единицу изделия и себестоимость
 .
Составить план выпуска изделий, дающий
предприятию максимальную прибыль.
.
Составить план выпуска изделий, дающий
предприятию максимальную прибыль.
4. Найти оптимальное распределение
ресурсов объемом не более 100 единиц
между 4 потребителями, если прибыль при
выделении i-му
потребителю
единиц ресурса равна
 млн. руб. При
млн. руб. При
 .
.
5. Динамическое программирование
Динамическое программирование представляет собой математический аппарат, позволяющий быстро находить оптимальное решение в случае, когда анализируемая ситуация не содержит факторов неопределенности, но имеется большое количество вариантов поведения, приносящих различные результаты, среди которых необходимо выбрать наилучший. Динамическое программирование подходит к решению некоторого класса задач путем их разложения на части, небольшие и менее сложные задачи. В принципе, задачи такого типа могут быть решены путем перебора всех возможных вариантов и выбора среди них наилучшего, часто такой перебор затруднителен. В этих случаях процесс принятия оптимального решения может быть разбит на шаги (этапы) и исследован с помощью метода динамического программирования.
Решение задач методом динамического программирования проводится на основе сформулированного Р.Э. Беллманом принципа оптимальности: оптимальное поведение обладает тем свойством, что каким бы ни было первоначальное состояние системы и первоначальное решение, последующее решение должно определять оптимальное поведение относительно состояния, полученного в результате первоначального решения.
Таким образом, планирование каждого шага должно проводиться с учетом общей выгоды, получаемой по завершении всего процесса, что и позволяет оптимизировать конечный результат по выбранному критерию.
Вместе с тем динамическое программирование не является универсальным методом решения. Практически каждая задача, решаемая этим методом, характеризуется своими особенностями и требует проведения поиска наиболее приемлемой совокупности методов для ее решения. Кроме того, большие объемы и трудоемкость решения многошаговых задач, имеющих множество состояний, приводят к необходимости отбора задач малой размерности либо использования сжатой информации.
Динамическое программирование применяется для решения таких задач, как: распределение дефицитных капитальных вложений между новыми направлениями их использования; разработка правил управления спросом или запасами; разработка принципов календарного планирования производства и выравнивания занятости в условиях колеблющегося спроса на продукцию; составление календарных планов текущего и капитального ремонтов оборудования и его замены; формирование последовательности развития коммерческой операции и т.д.
Пусть процесс оптимизации разбит на n
шагов. На каждом шаге необходимо
определить два типа переменных –
переменную состояния S
и переменную управления Х. Переменная
Sопределяет, в каких
состояниях может оказаться система на
данном k-м шаге. В
зависимости от S на
этом шаге можно применить некоторые
управления, которые характеризуются
переменной X. Применение
управления X на
k-м шаге приносит
некоторый результат
 и переводит систему в некоторое новое
состояние
и переводит систему в некоторое новое
состояние
 .
Для каждого возможного состояния на
k-м шаге среди всех
возможных управлений выбирается
оптимальное управление
.
Для каждого возможного состояния на
k-м шаге среди всех
возможных управлений выбирается
оптимальное управление
 такое, что результат, который достигается
за шаги с k-го по
n-й оказался
оптимальным. Числовая характеристика
этого результата называется функцией
Беллмана
такое, что результат, который достигается
за шаги с k-го по
n-й оказался
оптимальным. Числовая характеристика
этого результата называется функцией
Беллмана
 и зависит от номера шага k
и состояния системы S.
и зависит от номера шага k
и состояния системы S.
Все решение задачи разбивается на два этапа. На первом этапе, который называют условной оптимизацией, отыскиваются функция Беллмана и оптимальные управления для всех возможных состояний на каждом шаге, начиная с последнего.
После того, как функций Беллмана и соответствующие оптимальные управления найдены для всех шагов с n-го по первый, производится второй этап решения задачи, который называется безусловной оптимизацией.
В общем виде задача динамического
программирования формулируется следующим
образом: требуется определить такое
управление
 ,
переводящее систему из начального
состояния
,
переводящее систему из начального
состояния
 в конечное состояние
в конечное состояние
 ,
при котором целевая функция
,
при котором целевая функция
 принимает наибольшее (наименьшее)
значение.
принимает наибольшее (наименьшее)
значение.
Особенности математической модели динамического программирования заключается в следующем:
задача оптимизации формулируется как конечный многошаговый процесс управления;
целевая функция (выигрыш) является аддитивной и равна сумме целевых функций каждого шага:
 ;
;выбор управления
 на каждом шаге зависит только от
состояния системы к этому шагу
на каждом шаге зависит только от
состояния системы к этому шагу
 и не влияет на предшествующие шаги (нет
обратной связи);
и не влияет на предшествующие шаги (нет
обратной связи);состояние системы
 после каждого шага управления зависит
только от предшествующего состояния
системы
и этого управляющего воздействия
(отсутствие последействия) и может быть
записано в виде уравнения состояния:
после каждого шага управления зависит
только от предшествующего состояния
системы
и этого управляющего воздействия
(отсутствие последействия) и может быть
записано в виде уравнения состояния:
 ;
;на каждом шаге управления зависит от конечного числа управляющих переменных, а состояние системы зависит от конечного числа параметров;
оптимальное управление представляет собой вектор , определяемый последовательностью оптимальных пошаговых управлений:
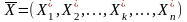 ,
число которых и определяет количество
шагов задачи.
,
число которых и определяет количество
шагов задачи.
Условная оптимизация. На данном
этапе отыскиваются функции Беллмана и
оптимальные управления для всех возможных
состояний на каждом шаге, начиная с
последнего в соответствии с алгоритмом
обратно прогонки. На последнем n-м
шаге найти оптимальное управление
 и значение функции Беллмана
и значение функции Беллмана
 не сложно, так как
не сложно, так как
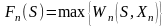 ,
где максимум ищется по всем возможным
значениям
,
где максимум ищется по всем возможным
значениям
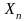 .
.
Дальнейшие вычисления производятся согласно рекуррентному соотношению, связывающему функцию Беллмана на каждом шаге с этой же функцией, но вычисленной на предыдущем шаге:
 .
.
Этот максимум (или минимум) определяется по всем возможным для k и S значениям переменной управления Х.
Безусловная оптимизация. После
того, как функция Беллмана и соответствующие
оптимальные управления найдены для
всех шагов с n-го по
первый (на первом шаге k=1
состояние системы равно ее начальному
состоянию S0),
осуществляется второй этап решения
задачи. Находится оптимальное управление
на первом шаге
 ,
применение которого переведет систему
в состояние
,
применение которого переведет систему
в состояние
 ,
зная которое можно, пользуясь результатами
условной оптимизации, найти оптимальное
управление на втором шаге, и так далее
до последнего n-го
шага.
,
зная которое можно, пользуясь результатами
условной оптимизации, найти оптимальное
управление на втором шаге, и так далее
до последнего n-го
шага.
5.1 Задача об оптимальном распределении инвестиций.
Требуется вложить имеющиеся Т единиц
финансовых средств в n
предприятий, прибыль
 от
которых в зависимости от количества
вложенных средств
от
которых в зависимости от количества
вложенных средств
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
|
|
|
… |
|
… |
|
|
… |
… |
… |
|
… |
… |
|
|
|
… |
|
… |
|
где - прибыль i-го предприятия при вложении в него средств.
Математическая модель задачи будет следующей.
Определить вектор , удовлетворяющий условиям
 ,
,
И обеспечивающий максимум целевой функции
 .
.
Процесс оптимизации разобьем на n
шагов, на k-м шаге будем
оптимизировать инвестирование не всех
предприятий, а только предприятий с
k-го по n-е.
При этом на них расходуются не все
средства, а некоторая меньшая сумма
 ,
которая и будет являться переменной
состояния системы. Переменной управления
на k-м шаге назовем
величину
,
которая и будет являться переменной
состояния системы. Переменной управления
на k-м шаге назовем
величину
 средств, вкладываемых в k-е
предприятие. В качестве функции Беллмана
средств, вкладываемых в k-е
предприятие. В качестве функции Беллмана
 на k-м шаге в этой
задаче можно выбрать максимально
возможную прибыль, которую можно получить
с предприятий с k-го
по n-е при условии, что
на их инвестировании осталось
на k-м шаге в этой
задаче можно выбрать максимально
возможную прибыль, которую можно получить
с предприятий с k-го
по n-е при условии, что
на их инвестировании осталось
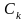 средств. При вложении в k-е
предприятие
средств получим прибыль
средств. При вложении в k-е
предприятие
средств получим прибыль
 ,
а система к (k+1)-му
шагу перейдет в состояние
,
а система к (k+1)-му
шагу перейдет в состояние
 ,
т.е. на инвестирование предприятий с
(k+1)-го до n-го
останется
,
т.е. на инвестирование предприятий с
(k+1)-го до n-го
останется
 средств.
средств.
Таким образом, на первом шаге условной
оптимизации при k=n
функция Беллмана представляет собой
прибыль только с n-го
предприятия. При этом на его инвестирование
может выделяться количество средств
,
 .
Чтобы получить максимум прибыли с этого
последнего предприятия, надо вложить
в него все эти средства, т.е.
.
Чтобы получить максимум прибыли с этого
последнего предприятия, надо вложить
в него все эти средства, т.е.
 и
и
 .
.
На каждом из последующих шагов для вычисления функции Беллмана следует использовать результаты предыдущего шага. Максимально возможная прибыль, которая может быть получена предприятиями с k-го по n-е, равна
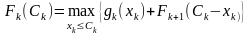 ,
,
 .
.
Максимум этого выражения достигается
на некотором значении
 ,
которое и является оптимальным управлением
на k-м шаге для состояния
системы
.
Аналогично можно отыскать функции
Беллмана и оптимальные управления
вплоть до шага
,
которое и является оптимальным управлением
на k-м шаге для состояния
системы
.
Аналогично можно отыскать функции
Беллмана и оптимальные управления
вплоть до шага
 .
.
Функция Беллмана
 представляет собой максимально возможную
прибыль со всех предприятий (с 1-го по
n-е), а значение
представляет собой максимально возможную
прибыль со всех предприятий (с 1-го по
n-е), а значение
 ,
на котором достигается максимум прибыли,
является оптимальным количеством
средств, которое необходимое вложить
в 1-е предприятие. Для всех последующих
шагов вычисляется величина
,
на котором достигается максимум прибыли,
является оптимальным количеством
средств, которое необходимое вложить
в 1-е предприятие. Для всех последующих
шагов вычисляется величина
 и оптимальным управлением на k-м
шаге является то значение
,
которое доставляет максимум прибыли
при соответствующем состоянии системы
.
и оптимальным управлением на k-м
шаге является то значение
,
которое доставляет максимум прибыли
при соответствующем состоянии системы
.
Пример 13. Распределить T=40 ден. ед. по трем предприятиям с целью получения максимальной суммарной прибыли. Прибыль с предприятий задается таблицей
Х |
|
|
|
0 |
0 |
0 |
0 |
10 |
17 |
21 |
19 |
20 |
23 |
25 |
24 |
30 |
34 |
30 |
29 |
40 |
40 |
37 |
32 |
Решение:
I этап. Условная оптимизация
I-й шаг. k=3.
Предполагаем, что все средства 40 ден.
ед. переданы на инвестирование третьего
предприятия. В этом случае максимальная
прибыль составит
 .
.
Таблица 2.
|
|
|
|
|||||
0 |
10 |
20 |
30 |
40 |
|
|
||
0 |
0 |
- |
- |
- |
- |
0 |
0 |
|
10 |
- |
19 |
- |
- |
- |
19 |
10 |
|
20 |
- |
- |
24 |
- |
- |
24 |
20 |
|
30 |
- |
- |
- |
29 |
- |
29 |
30 |
|
40 |
- |
- |
- |
- |
32 |
32 |
40 |
|
2-й шаг. k=2. Определяем оптимальную стратегию инвестирования во второе и третье предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид
 .
.
На его основе рассчитываются данные
Таблица 3.
|
|
|
|
||||
0 |
10 |
20 |
30 |
40 |
|||
0 |
0+0 |
- |
- |
- |
- |
0 |
0 |
10 |
0+19 |
21+0 |
- |
- |
- |
21 |
10 |
20 |
0+24 |
21+19 |
25+0 |
- |
- |
40 |
10 |
30 |
0+29 |
21+24 |
25+19 |
30+0 |
- |
45 |
10 |
40 |
0+32 |
21+29 |
25+24 |
30+19 |
37+0 |
50 |
10 |
3-й шаг. k=1. Определяем оптимальную стратегию инвестирования в первое и остальные предприятия. При этом рекуррентное соотношение Беллмана будет иметь вид
 .
.
На его основе находим данные.
Таблица 4.
|
|
|
|
||||
0 |
10 |
20 |
30 |
40 |
|||
0 |
0+0 |
- |
- |
- |
- |
0 |
0 |
10 |
0+21 |
17+0 |
- |
- |
- |
21 |
0 |
20 |
0+40 |
17+21 |
23+0 |
- |
- |
40 |
0 |
30 |
0+45 |
17+40 |
23+21 |
34+0 |
- |
57 |
10 |
40 |
0+50 |
17+45 |
23+40 |
34+21 |
40+0 |
63 |
20 |
II этап. Безусловная оптимизация
I-й шаг. По данным
таблицы 4 максимальный доход при
распределении 40 ден. ед. между тремя
предприятиями составляет
 .
При этом первому предприятию нужно
выделить
.
При этом первому предприятию нужно
выделить
 ден.ед.
ден.ед.
2-й шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю второго и третьего предприятий:
 ден. ед.
ден. ед.
По данным таблицы 3 находим, что оптимальный
вариант распределения денежных средств
размером 20 ден. ед. между вторым и третьим
предприятиями составляет
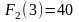 ден. ед. при выделении второму предприятию
ден. ед. при выделении второму предприятию
 ден. ед.
ден. ед.
3-шаг. Определяем величину оставшихся денежных средств, приходящуюся на долю третьего предприятия:
 ден. ед.
ден. ед.
Из таблицы 2 находим
 и
и
 ден. ед.
ден. ед.
Таким образом, оптимальный план
инвестирования предприятий
 ,
обеспечивающий максимальный доход,
равен
,
обеспечивающий максимальный доход,
равен
 ден. ед.
ден. ед.
5.2 Задача инвестирования
Предположим, что в начале каждого из
следующих n лет
необходимо сделать инвестиции Р1,
Р2, …,Рn.
Вы имеет возможность вложить капитал
в два банка: первый банк выплачивает
годовой сложный процент r1,
а второй – r2.
Для поощрения депозитов оба банка
выплачивают новым инвесторам премии в
виде процента от вложенной суммы.
Премиальные меняются от года к году, и
для i-го года равны
 и
и
 в первом и втором банках соответственно.
Они выплачиваются в конце года, на
протяжении которого сделан вклад, и
могут быть инвестированы в один из двух
банков на следующий год. Это значит, что
лишь указанные проценты и новые деньги
могут быть инвестированы в один из двух
банков. Размещенный в банке вклад должен
находится там до конца рассматриваемого
периода. Необходимо разработать стратегию
инвестиций на следующие n
лет.
в первом и втором банках соответственно.
Они выплачиваются в конце года, на
протяжении которого сделан вклад, и
могут быть инвестированы в один из двух
банков на следующий год. Это значит, что
лишь указанные проценты и новые деньги
могут быть инвестированы в один из двух
банков. Размещенный в банке вклад должен
находится там до конца рассматриваемого
периода. Необходимо разработать стратегию
инвестиций на следующие n
лет.
Элементы модели динамического программирования таковы.
Этапы i представляется порядковым номером года i, i=1, 2, …, n.
Вариантами решения на i-м этапе (для i-го года) являются суммы
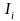 и
и
 инвестиций в первый и второй банк
соответственно.
инвестиций в первый и второй банк
соответственно.Состоянием на i-м этапе является сумма денег на начало i-го года, которые могут быть инвестированы.
По определению
 .
Следовательно,
.
Следовательно,

 (5.1)
(5.1)
где
 Сумма денег
,
которые могут быть инвестированы,
включает лишь новые деньги и премиальные
проценты за инвестиции, сделанные на
протяжении (i-1)-го
года.
Сумма денег
,
которые могут быть инвестированы,
включает лишь новые деньги и премиальные
проценты за инвестиции, сделанные на
протяжении (i-1)-го
года.
Пусть
 - оптимальная сумма инвестиций для
интервала от i-го до
n-го года при условии,
что в начале i-го года
имеется денежная сумма
.
Обозначим через
- оптимальная сумма инвестиций для
интервала от i-го до
n-го года при условии,
что в начале i-го года
имеется денежная сумма
.
Обозначим через
 накопленную сумму к концу n-го
года при условии, что
и
накопленную сумму к концу n-го
года при условии, что
и
 - объемы инвестиций на протяжении i-го
года в первый и второй банк соответственно,
- объемы инвестиций на протяжении i-го
года в первый и второй банк соответственно,
 .
.
Сформулируем задачу в следующем виде:
Максимизировать

где


Премиальные за n-й год
являются частью накопленной денежной
суммы от инвестиций, в выражения для
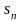 добавлены
добавлены
 и
и
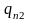 .
.
В данном случае рекуррентное уравнение для обратной прогонки в алгоритме динамического программирования имеет вид

где
 выражается через
в соответствии с формулой (5.1), а
выражается через
в соответствии с формулой (5.1), а
 .
.
Пример 14. Необходимо инвестировать 4000 долл. сейчас и 2000 долл. в начале каждого года, от второго до четвертого, считая от текущего года. Первый банк выплачивает годовой сложный процент 8% и премиальные на протяжении следующих четырех лет в размере 1,8; 1,7; 2,1 и 2,5% соответственно. Годовой сложный процент, предлагаемый вторым банком, на 0,2% ниже, чем предлагает первый банк, но его премиальные на 0,5% выше. Задача состоит в максимизации накопленного капитала к концу четвертого года.
Решение. Используя обозначения, имеем следующее.