
- •Математическое программирование.
- •Введение
- •1. Целочисленное программирование
- •Метод Гомори
- •Метод ветвей и границ
- •1.3 Задачи для самостоятельной работы
- •2. Теория игр
- •2.1. Основные положения теории игр
- •2.2. Решение матричной игры в чистых стратегиях
- •2.3. Решение матичной игры в смешанных стратегиях
- •2.4. Игра 2 2
- •2.5. Сведение матричной игры к задаче линейного программирования
- •2.6. Игры с природой
- •2.7. Задачи для самостоятельной работы
- •3. Линейный межотраслевой баланс
- •3.2. Задачи для самостоятельной работы
- •4. Нелинейное программирование
- •4.1 Постановка задача нелинейного программирования
- •4.2 Решение задач нелинейного программирования с ограничениями-равенствами
- •4.3. Решение задач нелинейного программирования с ограничениями-неравенствами
- •4.4. Задачи для самостоятельной работы
- •5. Динамическое программирование
- •Долл., долл.,
- •5.3 Задачи для самостоятельной работы
- •6. Контрольные задания
- •Литература
- •Содержание
- •Математическое программирование
2.5. Сведение матричной игры к задаче линейного программирования
Теория игр находится в тесной связи с линейным программированием, так как каждая конечная игра двух лиц с нулевой суммой может быть представлена как задача линейного программирования и решена симплексным методом и, наоборот, каждая задача линейного программирования может быть представлена как конечная игра двух лиц с нулевой суммой.
Рассмотрим игру двух лиц с нулевой суммой, заданную платежной матрицей
 .
.
Если платежная матрица не имеет седловой точки, т.е. и , то решение игры представлено в смешанных стратегиях и .
Применяя первым игроком оптимальной стратегии должно обеспечить ему при любых действиях второго игрока выигрыш не меньше цены игры.
 .
.
Рассмотрим задачу отыскания оптимальной стратегии игрока А, для которой имеют место ограничения

Величина
неизвестна, можно считать, что цена игры
 .
Последнее условие выполняется всегда,
если все элементы платежной матрицы
неотрицательны, а этого можно достигнуть,
прибавив ко всем элементам матрицы
некоторое положительное число. Преобразуем
систему ограничений, разделив все члены
неравенств на
.
.
Последнее условие выполняется всегда,
если все элементы платежной матрицы
неотрицательны, а этого можно достигнуть,
прибавив ко всем элементам матрицы
некоторое положительное число. Преобразуем
систему ограничений, разделив все члены
неравенств на
.
 (2.1)
(2.1)
где

По условию
 .
Разделим обе части этого равенства на
,
получим
.
Разделим обе части этого равенства на
,
получим
 .
.
Оптимальная стратегия игрока А должна максимизировать величину , следовательно, функция
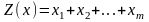 (2.2)
(2.2)
должна принимать минимальное значение.
Таким образом, получена задача линейного
программирования: найти минимум целевой
функции (2.2) при ограничениях (2.1), причем
на переменные наложено условие
неотрицательности. Решая ее, находим
значения
 и цену игры
и цену игры
 .
Тогда оптимальные стратегии находятся
по формулам
.
Тогда оптимальные стратегии находятся
по формулам
 .
.
Аналогично для второго игрока оптимальная стратегия должна обеспечить при любых стратегиях первого игрока проигрыш, не превышающий цену игры.

Преобразуем систему ограничений, разделив все члены неравенств на .
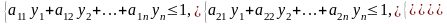 (2.3)
(2.3)
где

По условию
 .
Разделим обе части этого равенства на
,
получим
.
Разделим обе части этого равенства на
,
получим
 .
.
Оптимальная стратегия игрока В должна минимизировать величину , следовательно функция
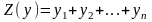 (2.4)
(2.4)
должна принимать максимальное значение.
Таким образом, получена задача линейного
программирования: найти максимум целевой
функции (2.4) при ограничениях (2.3), причем
на переменные наложено условие
неотрицательности. Решая ее, находим
значения
 .Оптимальные
стратегии находятся по формулам
.Оптимальные
стратегии находятся по формулам
 .
При этом цена игры
.
При этом цена игры
 .
.
Для нахождения решения игры имеем симметричную пару двойственных задач линейного программирования. Можно найти решение одной из них, а решение второй находится с использованием теории двойственности.
Пример
8. Фирма с учетом трех возможных
вариантов В1, В2,
и В3 поведение (стратегии)
партнера разработала также три стратегии
А1, А2 и А3
своей деятельности. Коэффициент
платежной матрицы представляет собой прибыль фирмы в
ситуации, в которой фирма применяет
стратегию Аi,
а ее партнер случайным образом для фирмы
применяет стратегию Вj.
Показать, что матричная игра не имеет
решения в чистых стратегиях и решить
ее в смешанных стратегиях, используя
эквивалентность матричной игры двух
игроков сводя к задаче линейного
программирования.
представляет собой прибыль фирмы в
ситуации, в которой фирма применяет
стратегию Аi,
а ее партнер случайным образом для фирмы
применяет стратегию Вj.
Показать, что матричная игра не имеет
решения в чистых стратегиях и решить
ее в смешанных стратегиях, используя
эквивалентность матричной игры двух
игроков сводя к задаче линейного
программирования.
Решение.
Вводя обозначения
 ,
находим:
,
находим:
 ,
т.е.
,
т.е.
 .
Следовательно, седлова точка отсутствует
и задача не имеет решения в чистых
стратегиях. Следует искать решение в
смешанных стратегиях: SA=(p1,p2,p3)
и SB=(q1,q2,q3).
.
Следовательно, седлова точка отсутствует
и задача не имеет решения в чистых
стратегиях. Следует искать решение в
смешанных стратегиях: SA=(p1,p2,p3)
и SB=(q1,q2,q3).
Обозначив
 и
и
 ,
составим две взаимно-двойственные
задачи линейного программирования
,
составим две взаимно-двойственные
задачи линейного программирования


Решаем симплексным методом одну из задач, например, задачу 2 (разрешающий элемент отмечен звездочкой).



Таким образом,
 и, следовательно, цена игры равна
и, следовательно, цена игры равна
 .
Оптимальную стратегию SB
находим из формул
.
Оптимальную стратегию SB
находим из формул
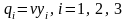 ,
т.е.
,
т.е.
 .
.
В соответствии с теоремами двойственных
задач линейного программирования и
приведенной симплексной таблицы имеем:
 и, следовательно, оптимальную стратегию
SA
находим по формуле
и, следовательно, оптимальную стратегию
SA
находим по формуле
 ,
т.е.
,
т.е.
 .
.
Проверка показывает, что
 и
и
 .
Таким образом, оптимальная стратегия
партнера банка SB=(0;
0,3077; 0,6923), самого банка SA=(0;
0,231; 0,769). Цена игры
.
Таким образом, оптимальная стратегия
партнера банка SB=(0;
0,3077; 0,6923), самого банка SA=(0;
0,231; 0,769). Цена игры
 .
.
