9. Обработка статистических данных методами линейной корреляции.

Предположим, что мы произвели одновременные измерения двух серий величин x и y. Разумеется, эти измерения были подвержены влиянию случайных ошибок. Как уже говорилось выше, причины возникновения случайных ошибок многочисленны и практически не поддаются учёту. Среди них могут быть ошибки, выражающие некоторую неизвестную нам закономерность, или ошибки, одновременно влияющие на обе величины. То есть эти серии измерений уже нельзя считать независимыми друг от друга. С другой стороны, сказать, что они связаны жёсткой функциональной зависимостью вида y=ax+b, тоже нельзя. В нашем случае взаимосвязь является статистической, т.е. при изменении величины x величина y имеет тенденцию также изменяться.

Эта тенденция соблюдается лишь в большей или меньшей степени, а в каждом конкретном случае возможны отклонения от неё. Зависимость в таких случаях называется корреляционной и характеризуется коэффициентом корреляции r (-1 ≤ r ≤ 1). Если r>0, то большим значениям x в среднем соответствуют большие значения y и наоборот. Чаще всего эта тенденция носит линейный характер. Если r=±1, то зависимость становится функциональной. При r<|0.2| можно считать, что величины не коррелированны.

Стоит заметить, что разговор в этой главе идет о наиболее частом случае корреляции – линейной корреляции. В случае корреляционной зависимости более высоких порядков (гиперболическая, параболическая) зависимости для коэффициента линейной корреляции могу не выполняться, а сам коэффициент рассчитывается более сложным образом.

Численное значение коэффициента r можно найти из специально организованных наблюдений. В штурманской практике нередко возникает необходимость учёта корреляционной зависимости при решении ряда навигационных задач, в первую очередь в вопросах оценки точности обсервации.

Для определения коэффициента корреляции необходимо измерить при более или менее идентичных условиях n парных значений двух навигационных параметров x_i и y_i (например, два пеленга береговых ориентиров). После определённой статистической обработки данных коэффициент корреляции рассчитывается по формуле:

, ( 9.0)

где v_xi и v_yi уклонения величин x_i и y_i от вероятнейших значений соответственно.

Сама зависимость будет задаваться уравнением линейной регрессии:

, ( 9.0)

где и вероятнейшие значения измеряемых величин.

Смысл уравнения линейной регрессии можно выразить так, каждому значению x_i с наибольшей вероятностью будет соответствовать значение y_xi.

Теперь обратимся к такому важному случаю, когда некоторая искомая величина a определяется, как функция непосредственно измеряемых величин x, y: a=f(x, y).

Предположим, что величины x, y коррелированны, т.е. если налицо взаимная зависимость случайных ошибок в аргументах x и y, в этом случае, СКП величины a определяется следующим образом:

( 9.0)

В случае отсутствия корреляционной связи между величинами x и y, формула (9.3) примет вид (5.1).

Пример 9.14

Дано: две серии пеленгов ИП1, ИП2.

ИП1	30.8°	34.9°	36.5°	39.2°	38.9°	40.0°	45.8°	44.1°
ИП2	81.0°	78.8°	78.2°	85.0°	80.6°	84.4°	83.5°	87.7°

Найти:

1. вероятнейшие значения измеренных величин;

2. коэффициент корреляции между пеленгами;

3. составить уравнение линейной регрессии, построить график;

4. СКП каждого навигационного параметра;

5. рассчитать вероятнейшее значение горизонтального угла ;

6. рассчитать СКП вероятнейшего значения горизонтального угла .

Решение:

1. Составляем расчётную таблицу:

• во вторую и восьмую колонку вводим ИП2 и ИП1 соответственно и рассчитываем вероятнейшее значение (среднее арифметическое) каждой величины;

• в третьей и седьмой колонках рассчитываем соответствующие уклонения вышеперечисленных величин;

• в четвёртой и шестой колонках квадраты уклонений;

• в пятой их произведения;

• внизу 4 – 6 колонок находим их суммы.

Таблица 9.16

1	2	3	4	5	6	7	8
n	ИП2	vип2	v^2ип2	vип2*vип1	v^2ип1	vип1	ИП1
1	81.0	1.4	2.0	11.2	63.6	8.0	30.8
2	78.8	3.6	13.0	14.0	15.0	3.9	34.9
3	78.2	4.2	17.6	9.6	5.2	2.3	36.5
4	85.0	-2.6	6.8	1.1	0.2	-0.4	39.2
5	80.6	1.8	3.2	-0.2	0.0	-0.1	38.9
6	84.4	-2.0	4.0	2.4	1.5	-1.2	40.0
7	83.5	-1.1	1.2	7.7	49.4	-7.0	45.8
8	87.7	-5.3	28.1	28.2	28.4	-5.3	44.1
	82.4		75.86	73.95	163.2		38.8

2. По формуле (9.1) находим коэффициент корреляции:

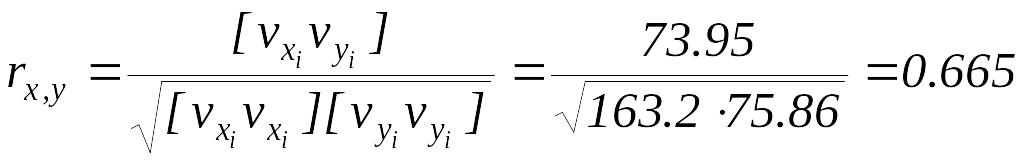
3. Составляем уравнение линейной регрессии

ИП1
30.8	79.9
34.9	81.2
36.5	81.7
39.2	82.5
38.9	82.4
40.0	82.8
45.8	84.6
44.1	84.0

Строим зависимость от ИП₁

4. По формуле (4.2) рассчитываем СКП единичных значений

;

и формуле (4.7) СКП вероятнейших значений пеленгов.

5. Рассчитываем значение горизонтального угла .

6. Рассчитываем СКП горизонтального угла 

• без учёта корреляционной зависимости по формуле (5.1);

Находим частные производные пеленгов:

;

• и с учётом корреляционной зависимости по формуле (9.3)

Как видим, учёт корреляционной зависимости даёт нам меньшее значение погрешности.