Глава 5. Нечеткая информация и нечеткие выводы.

В настоящее время наблюдается тенденция внедрения нечетких систем не только в промышленности, но и в непромышленных областях деятельности человека. Весьма актуально применение теории нечетких множеств в медицине, охране окружающей среды, защите от стихийных бедствий, обучении и многих других областях для обработки информации, диагностики, оценки, прогнозирования и моделирования.

Отличительная особенность нечетких систем состоит в том, что помимо объективных законов в их функционировании существенную роль играют субъективные представления и суждения людей.

Почти все понятия в естественном языке и наши знания в большинстве областей являются нечеткими.

В традиционной математике невозможно моделирование реальных сложных систем, так как в ней нет средств адекватного описания понятий, которыми пользуется человек, и которые имеют неопределенный смысл. Для успешного применения математических методов для анализа сложных систем необходимо создание средств учета нечетких представлений и суждений людей о реальном мире в математических моделях.

Математическая теория нечетких множеств позволяет оперировать нечеткими знаниями и делать нечеткие выводы. Эта теория составляет основу одной из современных передовых технологий и является новым средством связи человека с информационными системами. Это единственная теория, которая математически оперирует со смысловым содержанием слов, представляет смысловые нечеткости слов, позволяет математически обрабатывать субъективные данные.

В настоящее время применение теории нечетких множеств в медицине имеет важное значение для улучшения медицинской диагностики, оценки действия лекарственных препаратов, создания искусственных органов, анализа риска, оценки состояния окружающей среды и др. Нечеткое рассуждение обеспечивает более интуитивный способ трактования нечетких данных и, как следствие, более точное приближение клинической реальности.

Способность человека принимать правильные решения в реальных ситуациях, содержащих большое количество неопределенностей и неточностей, требует создания математической теории, учитывающей и моделирующей приближенные рассуждения человека.

В 1965г. Л.Заде опубликовал в журнале “InformationandControl” статью “FuzzySets” (“Нечеткие Множества”), которая явилась основополагающей работой для нового направления в прикладной математике, получившего название теории нечетких множеств.

Математическая теория нечетких множеств позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы.

Заде ввел понятие нечеткого множества, характеристическая функция которого может принимать не только значения 0 или 1, но любые значения выше 0 и ниже 1 в интервале [0, 1]. Вместо термина «характеристическая функция» Заде использовал термин «функция принадлежности». Заде определил ряд операций над нечеткими множествами и предложил обобщение известных методов логического вывода modusponensиmodustollens.

Для анализа ситуаций, в которых определяющими являются качественные, а не количественные характеристики, Заде ввел понятие лингвистической переменной, лингвистическими значениями которой (термами) являются нечеткие множества.

Нечеткие множества.

Пусть Х – множество элементов, называемое полным пространством или универсальным множеством, xявляется элементом Х, а соответствующие обозначения:

xX– элементxпринадлежит множествуX,

X= {x} –Xявляется совокупностьюx.

Четкое множество Aв полном множествеXопределяется с помощью характеристической функции_A(x), принимающей значение 1, еслиxX, и 0 – в противном случае. МножествоAопределяется как множество упорядоченных пар:

Пример. Пусть множество чиселA= {x| 0x2}. Функция принадлежности этого множества представлена на рис. 5.1 ,а.

_A_A

1 1

0 2 x0 1x

Рис. 5.1 Определение нечеткого множества с помощью характеристической функции.

(а) (б)

Заде расширил двузначную оценку 0 или 1 до неограниченной многозначной оценки выше 0 и ниже 1 в [0, 1]. Нечеткое множество Aполного множестваXопределяется как множество упорядоченных пар:

,

где xX, а_A(x) – функция принадлежности, принимающая значения в некотором упорядоченном множествеM, например,M= [0, 1]. Значение_A(x) этой функции для конкретного элементаxназывается степенью принадлежности этого элемента нечеткому множествуA. МножествоMназывается множеством принадлежностей. Четкое множество является частным случаем нечеткого множества, для негоM= {0, 1}.

Пример. Пусть нечеткое множество чиселA= {x| «значенияxблизки к 1»}. Функция принадлежности этого нечеткого множества представлена на рис. 5.1,б.

Нечеткое множество можно представить в виде записи. Например, пусть X= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} иA– нечеткое множество «маленьких чисел». ТогдаAможно представить в видеA= {(1/0), (1/1), (0,8/2), (0,5/3), (0,1/4)} илиA= 1/0 + 1/1 + 0,8/2 + 0,5/3 + 0,1/4. Здесь, например, 0,8/2 означает_A(2) = 0,8. При этом опускают члены со значениями функции принадлежности, равными 0. В этой записи знак «+» не является обозначением операции сложения, а имеет смысл объединения.

Нечеткое множество называетсяпустым, если его функция принадлежности равна нулю на всем множествеX, т.е.

_A(x) = 0, x  X .

Носителемнечеткого множестваA(обозначениеsuppA) является обычное множество со свойством_A(x)0, т.е.

supp A = {x | _A(x)  0}, x  X .

Нечеткое множество Aназываетсянормальным, если его высотаsup_A(x) равна 1,

В противном случае нечеткое множество называется субнормальным. Непустое субнормальное множество можно нормализовать, разделив функцию принадлежности этого множества_A(x) на величину.

Нечеткое множество унимодально, если_A(x) = 1 только на одномxизX. ЭлементыxX, для которых_A(x) = 0,5, называютсяточками переходамножестваA.

Пример. ПустьX= {0, 1, 2,, 10},M= [0, 1]. Нечеткое множество «несколько» можно определить следующим образом: «несколько» = 0,5/3 + 0,8/4 + 1/5 + 1/6 + 0,8/7 + 0,5/8; его характеристики: высота = 1, носитель = {3, 4, 5, 6, 7, 8}, точки перехода = {3, 8}.

Как видно из приведенного определения, нечеткое множество строго определяется с помощью функции принадлежности, которая принимает значения из интервала [0, 1]. Нечеткое множество, значения функции принадлежности которого имеют точную оценку в [0, 1], называются множествами типа 1.

Л. Заде определил нечеткое множество типа 2, у которого значениями функции принадлежности является нечеткое множество над значениями оценки в интервале [0, 1]. Продолжая обобщение, Л. Заде предложил нечеткое множество типа n,n= 1, 2, 3,, значениями функции принадлежности которого являются нечеткие множества типаn– 1.

В приближенных рассуждениях не обязательно использовать числовые оценки. Можно использовать лингвистические значения истинности (например, более или менее истинно, не очень истинно, совершенно ложь), выраженные посредством нечетких подмножеств единичного интервала.

Операции над нечеткими множествами.

Рассмотрим наиболее распространенные операции над нечеткими множествами. Пусть AиBнечеткие множества на универсальном множествеX, а μ_A(x) и μ_B(x) – их функции принадлежности, соответственно.

Логические операции.

Включение.

Дополнение.

Дополнением нечеткого множества A в Xназывается нечеткое множествоBс функцией принадлежности вида

x  X _A(x) = 1 - _B(x).

Дополнение обозначается как или.

Пересечение.

Пересечением нечетких множеств A и BвXназывается нечеткое множествоABс функцией принадлежности вида

AB– наибольшее нечеткое множество, содержащееся одновременно вAиB.

Объединение.

Объединением нечетких множеств A и B в Xназывается нечеткое множествоABс функцией принадлежности

AB– наименьшее нечеткое множество, включающее какA, так иB.

Графическое изображение логических операций над нечеткими множествами представлено с помощью колоколообразной функции принадлежности на рис. 5.2.

1.0 _B (x) 1.0 _Ā (x)

_A (x) _A (x)

0 X 0 X

a б

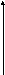
_A (x) _B (x) _A (x) _B (x)

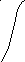
1.0 1.0

_AB (x)

_AB (x)

0 Х 0X

в г

Рис. 5.2. Основные логические операции над нечеткими множествами.

а – включение AB, б – дополнительное нечеткое множество, в – пересечение нечетких множествAB, г – объединение нечетких множествAB.

Для операций пересечения и объединения, определенных над нечеткими множествами, справедливы следующие свойства:

1. идемпотентность

A  A = A; A  A = A;

2. коммутативность

A  B = B  A; A  B = B  A;

3. ассоциативность

A  (B  C) = (A  B)  C;

A  (B  C) = (A  B)  C;

4. дистрибутивность

A  (B  C) = (A  B)  (A  C);

A  (B  C) = (A  B)  (A  C);

5. A=A, где- пустое множество, т. е._(x) = 0xX;

A   = ;

6. AX=A, гдеX– универсальное множество;

A  X = X;

7. – формулы де Моргана.

Алгебраические операции над нечеткими множествами.

Алгебраическое произведение A*Bопределяется следующим образом:

Алгебраическая сумма определяется следующим образом:

Для операций не выполняются свойства идемпотентности и дистрибутивности.

Унарная операция возведения в степень нечеткого множестваA(- положительное число) определяется следующим образом:

x  X .

Частным случаем возведения в степень являются:

• операция концентрирования (уплотнения);

• операция растяжения ,

графически представленные на рис. 5.3. Операция концентрирования уменьшает «нечеткость» множества, уточняет диапазон его определения. Операция растяжения расширяет диапазон определения.

Умножение на число. Если- положительное число, такое, что, то нечеткое множествоимеет функцию принадлежности:

1.0

A²

AA^0.5

0

X

Рис. 5.3. Операции концентрирования и растяжения.

.

Выпуклая комбинация нечетких множеств.

Пусть A₁,A₂, …,A_n– нечеткие множества универсального множестваX, а ω₁, ω₂, …, ω_n– неотрицательные числа, сумма которых равна 1.

Выпуклой комбинацией A₁,A₂, …,A_nназывается нечеткое множествоAс функцией принадлежности:

x  X

Декартово произведение A₁A₂A_nнечетких множествA₁,A₂, …,A_n универсальных множествX₁,X₂, …,X_n, соответственно, определяется как нечеткое множествоAуниверсального множестваX=X₁X₂X_nс функцией принадлежности:

Четкое множество  – уровня (или уровня )

Множеством  – уровня нечеткого множестваAуниверсального множестваXназывается четкое множествоA_универсального множестваX, составленное из элементовxX, степени принадлежности которых нечеткому множествуAне меньше числа. Множество- уровняA_определяется как

A_ = x  _A(x)   x  X, где   1

Пример.ПустьA= 0.2/x₁+ 0/x₂+ 0.5/x₃+ 1/x₄.

Тогда A_0.3 = x₃, x₄, A_0.7 = x₄.

Если ₁ ₂, тоA_1A_2.

Нечеткие отношения.

Нечеткое отношение представляет собой важное математическое понятие, позволяющие формулировать и анализировать математические модели реальных задач принятия решений. Отношение на множестве альтернатив в таких задачах выявляется обычно путем консультаций с лицом, принимающим решения, или с экспертом, которые зачастую не имеют вполне четкого суждения об этом отношении. В подобных случаях нечеткое отношение может служить удобной и более адекватной реальности формой представления исходной информации, чем обычное отношение.

Начнем изложение с обычного отношения, которое будем называть просто отношением.

Отношением R на множестве X называется декартово произведение

XX. Задать отношение на множествеXозначает указать все пары элементовx,yXтакие, чтоxиyсвязаны отношениемR. Для обозначения того, что элементыxиyсвязаны отношениемR, можно воспользоваться двумя эквивалентными значениями:xRyили (x,y)R.

Если множество X, на котором задано отношениеR, конечно, то это отношение удобно описывать матрицей, представляющей собой характеристическую функцию множестваRXX. Элементы этой матрицы определяются следующим образом:

.

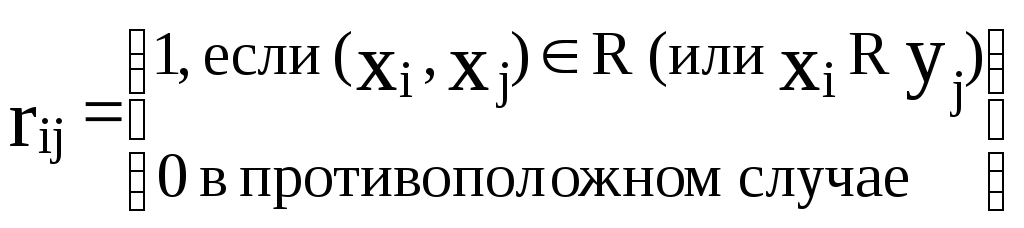Пусть E=E₁E₂E_n– декартово произведение универсальных множеств иM– некоторое множество принадлежностей (например,M= [0, 1]). Нечеткое парное отношение определяется как нечеткое подмножествоRнаE, принимающее свои значения вM. В случаеn= 2 иM= [0, 1], нечетким отношениемRмежду множествамиX=E₁иY=E₂будет называться функцияR: (X,Y)[0, 1], которая ставит в соответствие каждой паре элементов (x,y)XYвеличину.

Нечеткое отношение XYзаписывается в виде:xX,yYxRy. В случае когдаX=Y, т.е.XиYсовпадают, нечеткое отношениеR:XX[0,1] называется нечетким отношением на множествеX.

Пример.Пусть,,M= [0, 1]. Нечеткое отношениеR=XRYможет быть задано следующим образом:

R	y1	y2	y3	y4
x1	0	0	0.1	0.3
x2	0	0.8	1	0.7
x3	1	0.5	0.6	1

Обычное отношение можно рассматривать как частный случай нечеткого отношения, функция принадлежности которого принимает лишь значения 0 или 1.