Установление функции принадлежности для вывода

Норм Хр.геп. Агр.геп. Цирроз

1

0

0 10 20 30 40 50

Рис. 5.8. Шаги в нечетком рассуждении.  = не используется.

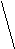
1 1 1

49. 0.59 0.42 0.52 0.62 0.34 0.60

Малое Среднее Большое

0 0 0

Рис. 5.9. Функции принадлежности для предположений лев/прав отношения

Нечеткое множество Большое отмечается как 1 для чисел больше среднего значения для пациентов с острой формой болезни и как нуль для среднего значение минус одно среднеквадратичное отклонение. Нечеткое множество Среднее строится в виде треугольника. Среднее значение свойства для пациентов с хронической формой болезни отмечается как единица и любое значение в диапазоне среднее значение среднеквадратичное отмечается как нуль.

Для определения категории состояния пациента у объекта измерялись значения свойств сцинтиграммы и затем выполнялись 4 этапа.

1 этап. Вводилась нечеткость для измеренных четких значений свойств, т.е. определялась степень их принадлежности к членам предпосылки каждого правила.

2 этап. Вычислялся уровень «отсечения» для предпосылки каждого правила как результат операции МИНИМУМ для лингвистических значений свойства.

3 этап. Полученные «отсечением» заключения каждого из четырех правил сводились к одному нечеткому множеству посредством операции МАКСИМУМ.

4 этап. Дефаззификация была выполнена методом вычисления центра тяжести.

Рассмотренные до сих пор нечеткие выводы представляют собой восходящие выводы от предпосылок к заключениям:

(Знание) Если xестьA, тоyестьB

(Факт) xестьA’



(Вывод) y есть B’ (восходящий нечеткий вывод)

Такие выводы наиболее часто используются на практике. В последние годы в диагностических нечетких экспертных системах начинают применять нисходящие выводы:

(Знание) Если xестьA, тоyестьB

(Факт) yестьB’



(Вывод) x есть A’ (нисходящий нечеткий вывод)

По существу это метод моделирования с помощью уравнения нечетких отношений.

Рассмотрим нисходящий нечеткий вывод на примере диагностической системы. Пусть полное пространство предпосылок Xсостоит изmфакторов, а полное пространство заключений – изnсимптомов:

X= {x₁,x₂,,x_m}, (5.22)

Y= {y₁,y₂,,y_n} (5.23)

Возьмем упрощенную модель диагностики неисправности автомобиля при m= 2 иn= 3:

x₁– неисправность аккумулятора,

x₂– отработка машинного масла,

y₁– затруднения при запуске,

y₂– ухудшение цвета выхлопных газов,

y₃– недостаток мощности.

Между каждым членом предпосылок x_iи каждым членом заключенийy_jсуществуют нечеткие причинные отношенияr_ij=x_iy_j. Все нечеткие отношения можно представить в виде матрицыRсmстроками иnстолбцами. То есть, имеем матрицу нечетких отношений:

R = [r_ij], r_ij  [0, 1], i = 1, , m; j = 1, , n. (5.24)

Предпосылки будем рассматривать как входы, а заключения – как выходы нечеткой системы, показанной на рис. 5.10. Предпосылки и заключения можно рассматривать как нечеткие множества AиBна пространствахXиY. Отношения этих множеств можно представить в виде

B = A  R (5.25)

где «» обозначает правило композиции нечетких выводов, например,max-minкомпозицию. При этом направление выводов является обратным по отношению к направлению выводов для правил. То есть, в случае диагностики задана матрицаR(знания эксперта), наблюдаются выводыB(симптомы) и определяются входыA(факторы).

В приведенном выше примере диагностики неисправностей автомобиля модель диагностики системы состоит из двух предпосылок и трех заключений: X= {x₁,x₂},Y= {y₁,y₂,y₃}. Знания эксперта-механика преобразуются в матрицу нечетких отношений и имеют вид:

(5.26)

Пусть в результате осмотра автомобиля его состояние можно оценить как

B = 0,9/y₁ + 0,1/y₂ + 0,2/y₃ . (5.27)

Необходимо найти причину такого состояния:

A = a₁/x₁ + a₂/x₂ . (5.28)

В этом случае формулы (5.27) и (5.28) можно представить в виде нечетких векторов-строк:

B= [0,9 0,1 0,2], (5.29)

A= [a₁,a₂]. (5.30)

Тогда формулу (5.25) можно представить в виде

(5.31)

либо, транспонируя, в виде нечетких векторов-столбцов

(5.32)

Здесь также в качестве правила композиции нечетких выводов «» изучаются различные способы, но традиционно чаще используют композицию максимум-минимум. В этом случае формулы (5.31) или (5.32) преобразуются в вид

0,9 = (0,9 a₁)(0,6a₂), (5.33)

0,1 = (0,1 a₁)(0,5a₂), (5.34)

0,2 = (0,2 a₁)(0,5a₂), (5.35)

что можно рассматривать как моделирование с помощью системы уравнений первого порядка, если заменить сложение на максимум, а умножение на минимум. Решим эту систему. Заметим, что в уравнении (5.33) второй член правой части не влияет на левую часть, поэтому

0,9 = 0,9 a₁,a₁0,9 (5.36)

Из уравнения (5.34) получим

0,1 0,5a₂,a₂0,1. (5.37)

Формулы (5.36) и (5.37) удовлетворяют третьему уравнению (5.35). Таким образом, получаем решение

1,0 a₁0,9, 0a₂0,1, (5.38)

т.е. лучше заменить аккумулятор (a₁– мера неисправности аккумулятора,a₂– мера отработки машинного масла).

На практике mиnпринимают значения от нескольких единиц до нескольких десятков, могут одновременно использоваться различные правила композиции нечетких выводов и сама схема выводов может быть многокаскадной.

Входы Выходы

R = ( r _ij )

i = 1 ~ m

j = 1 ~ n

x₁oy₁

x₂oy₂

 

x_i o y_j

 

x_m o y_n

A R B

(нечеткое (нечеткое (нечеткое

множество множество множество

в X) в X Y) в Y)

Рис. 5.10 Моделирование с помощью нечеткой системы :

В данном примере решение получено как значения в отрезке (выражение (5.38)), в результате можно предложить максимальное [1,0 0,1] или минимальное решение [0,9 0]. В общем случае очевидно, что для композиции максимум-минимум существует единственное максимальное и несколько «меньших» решений. На практике количество методов решения систем уравнений нечетких отношений значительно меньше, чем количество методов выводов по правилам, и в настоящее время пока не поставляются программы для решения таких систем.

В работе (Лосев) для решения задачи оценки качества лекарственных препаратов при их испытаниях на безвредность и переносимость использовались элементы теории нечетких множеств. На этапе применялся нечеткий восходящий вывод для классификации качества воздействия препаратов. Наэтапе выполнялось построение полиномиальных моделей, описывающих зависимость качества реакции от схемы применения фармакологических средств.

Оценка лекарственного препарата производилась по каждому показателю качества следующим образом.

Использовались две величины, определяющие качество реакции:

• нормированная величина показателя на пике реакции di,

• разность между значением показателя на пике реакции и его исходной величиной di.

На основе этих величин можно составить 2 группы функций принадлежности. Для решения поставленной задачи была разработана методика, основанная на методе Харрингтона и теории нечетких множеств. Для установления первой группы функций принадлежности использовалась шкала желательности Харрингтона, состоящая из подмножеств А, В, С, характеризующих величину исследуемого показателя на пике реакции (d). На множестве [0, 1] была определена лингвистическая переменная «желательность». Лингвистические значения этой переменной аналогичны смысловым значениям подмножеств А, В, С и, следовательно, смысловым значениям шкалы Харрингтона (рис. 5.11, а). Вторая группа функций принадлежности основана на множествахD,E,F,G, характеризующих изменение величины показателя по сравнению с исходным уровнем (d). Границы между этими множествами и вид соответствующих им функций принадлежности выбраны экспертным методом (рис. 5.11, б).



На следующем шаге осуществляется классификация типов реакции на основе операции конъюнкции лингвистических значений параметровdиd, как показано в таблице 5.1.



1

A

B

C

d

0

0.2

0.63

Рис. 5.11(а). Множества, характеризующие исследуемый показатель на пике реакции.



1

D

E

F

G

d

-0.5

-0.1

0

0.7

Рис. 5.11(б). Множества, характеризующие изменение величины показателя по сравнению с исходным уровнем.

Таблица 5.1.

Логические правила классификации реакций.

Реакция	Условие	Критерий оценки:
очень хорошо	AD
хорошо	A E BD
удовлетворительно	A F BE
плохо	BF
Очень плохо	B G C  F C  G

Алгоритм принятия решения состоит в следующем. Исследуется выборка объектов. Измеряются показатели состояния человека у каждого объекта выборки. Составляется матрица значений функций принадлежности (d), оценивающих степень принадлежности каждого показателя к каждому классу по всем объектам, и аналогичная матрица оценок функций принадлежности(d). На основании операции конъюнкции все объекты относятся по каждому показателю к определенному классу. Пример использования данной процедуры представлен в таблице 5.2 на основе результатов оценки реакции испытуемых по содержанию в крови сегментоядерных нейтрофилов в условиях действия препарата «реаферон».

Аналогичные таблицы составляются для всех показателей. Таким образом, могут быть получены качественные оценки воздействия препарата по каждому исследуемому показателю для каждого исследуемого объекта.

Полученные качественные оценки в дальнейшем преобразуются в баллы. В таблице 5.3 показано соответствие между классами и балльными оценками, причем лучшему классу присваивается меньший балл с целью последующей минимизации полученного результата по факторам.

После вычисления балльной оценки показателя у каждого испытуемого проводилось усреднение этой оценки по всем объектам выборки. Тем самым

Таблица 5.2.

Результаты классификации реакций.

N Испытуемых	Оценка реакции			Оценка
	d	d
1	0.61	-0.28		Плохо
2	0.99	0.02		Хорошо
3	0.89	-0.11		Удовлетвори-тельно
4	0.49	-0.2		Плохо
5	0.97	0.25		Очень хорошо
6	0.61	0.24		Хорошо
7	1.00	0.62		Очень хорошо

определялся усредненный отклик каждого показателя на конкретную комбинацию воздействующих факторов.

Таблица 5.3.

Преобразование классов в балльные оценки

Классы типов реакций	Балльные оценки
Очень хорошо	1
Хорошо	2
Удовлетворительно	3
Плохо	4
Очень плохо	5

На этапе для каждой оценки качества реакции по соответствующему показателю строилась полиномиальная модель, количественно описывающая зависимость балльной оценки реакции от комплексного влияния факторов, определяющих схему применения препарата, например: доза, кратность введения и т.д. Все расчеты выполнялись на основе методологии математического планирования эксперимента.

По результатам спланированного эксперимента строится система полиномиальных моделей:

В качестве функции отклика (y_m) рассматривается балльная оценка качества реакции, полученная на основании использования функции Харрингтона и теории нечетких множеств.

Среди полиномиальных моделей выбирается целевая функция

y _i = f _i (x ₁, x ₂, , x _n) ,

которая должна отражать эффективность препарата и стремиться к максимуму, например, фагоцитарный индекс, характеризующий неспецифическую резистентность организма. На остальные функции накладываются односторонние ограничения вида:

y _i = f _i (x ₁, x ₂, x _n)  y _{i max} ,

где y_{i max}– пороговая балльная оценка реакции.

В конечном итоге рассчитывается оптимальное сочетание значений воздействующих факторов, являющихся параметрами схемы применения препарата. Для решения задачи оптимизации были разработаны алгоритм и компьютерная программа на основе использования метода Дэвидона–Флетчера-Пауэлла. Этот метод переменной метрики применялся в сочетании с методом одномерного поиска ДСК-Пауэлла (Коггина).

Нечеткие и лингвистические переменные.

В теории нечетких множеств для описания объектов и явлений используются нечеткие и лингвистические переменные.

Нечеткая переменная характеризуется тройкой параметров (X, U, A) , где X – название переменной, U – универсальное множество, на котором определена переменная X, A – нечеткое множество на U, описывающее ограничения на значения нечеткой переменной X

Нечеткие числа – это нечеткие переменные, определенные на множестве действительных чисел.

Лингвистической называется переменная, значениями которой являются слова или предложения. Совокупность ее лингвистических значений (термов) составляет терм – множество. Лингвистическая переменная более высокого порядка, чем нечеткая переменная, так как значениями лингвистической переменной являются нечеткие переменные.

Лингвистическая переменная характеризуется набором параметров (, T, U, G, M), в котором- название лингвистической переменной; T – терм – множество, т.е. множество лингвистических значений (нечетких переменных), областью определения каждого из которых является множество U; G – синтаксическая процедура, позволяющая генерировать новые термы; M – семантическая процедура, позволяющая для каждой нечеткой переменной сформировать соответствующее нечеткое множество.

Пример. Лингвистическая переменная Возраст определена на U = [0, 100]; ее термами являются: молодой, средний, старый. Новые термы образуются с помощью союзов «и», «или» и модификаторов «очень», «вполне» и др. Смысл каждого лингвистического значения характеризуется нечетким множеством.

Л. Заде определил лингвистическую переменную истинность, значения которой назваллингвистическими значениями истинности. Трактовка истинности как лингвистической переменной приводит к нечеткой логике и приближенным рассуждениям.

Косвенные нечеткие выводы.

В настоящее время во многих экспертных системах используются косвенные нечеткие выводы. Рассмотрим их применение на следующем примере.

При разработке новых лекарственных препаратов требуется проведение квалифицированных исследований безвредности данных препаратов и эффективности их воздействия. Необходимо оценить влияние препарата на пациента по показателям жизнедеятельности организма человека и отрегулировать схему применения лекарства, определяемую воздействующими факторами, такими как доза, кратность введения, длительность применения и т.д. При этом измеренные числовые данные часто являются неточными из-за нечеткости измерений и интерпретации числовых значений.

Экспертами устанавливаются численные интервалы для характеристик нормальности состояния организма, определяются пределы значений показателей для «нормы» и для отклонений от «нормы». При этом границы интервалов являются размытыми вследствие зависимости от процедур измерения, от специалиста, проводящего измерения, и от используемых приборов. Для реализации этих проблем теория нечетких множеств предлагает метод нечеткого вывода с помощью лингвистических правил, заменяющих количественные модели, и косвенных методов.

В работе (Лосев, Чурносов) нечеткие выводы использовались для управления воздействующими факторами, определяющими схему применения препарата. Наблюдались показатели состояния организма на пике реакции и их отклонения от исходного состояния.

Знания экспертов могут быть представлены в виде лингвистических правил:

Правило 1: если Пок1 есть P₁, то ∆uестьP_u1

Правило 2: если ∆Пок1 есть P₂, то ∆uестьP_u2

Здесь Пок1 – показатель состояния организма на пике реакции; ∆Пок1 – отклонение значения показателя на пике реакции от его начального состояния; ∆u– рекомендуемое изменение фактора воздействия, например, дозы лекарственного препарата;P₁,P₂иP_u1,P_u2– нечеткие множества, которые имеют функции принадлежности предпосылки и заключения, соответственно.

Функции принадлежности, построенные для набора используемых показателей состояния организма, для нормальных и патологических состояний, запоминаются как база знаний.

Нечеткий вывод можно представить следующим образом:

Здесь Правило является нечетким продукционным правилом типа «если…то…», в котором выражение, стоящее послеесли, является предпосылкой, условием, антецедентом, а выражение стоящее послето, заключением, операцией, действием.D₁иC₁– нечеткие (лингвистические) переменные.

Смысл формулы, представляющей нечеткий вывод, заключается в том, что при наличии нечеткого продукционного правила и D₁в качестве нечеткого входного значения определяется заключение, нечеткое выходное значениеC₁.

Нечеткий вывод является прямым, когда значение принадлежности нечеткого множества трактуется как значение истинности и вывод осуществляется при непосредственном использовании этого значения.

В приближенных рассуждениях можно применять нечеткое представление значения истинности и рассматривать лингвистические значения истинности (например: более или менее истинно, не очень истинно, совершенно ложь), выраженные посредством нечетких подмножеств единичного интервала.

Нечеткий вывод называется косвенным, когда он производится с использованием лингвистического значения истинности. Например, наблюдение «Пок1 есть D₁» может быть представлено нечетким суждением «реакция исследуемого показателя удовлетворительна – довольно истинно».

В случае косвенного вывода определяется истинность нечетких суждений. Пусть - нечеткое множество единичного интервалаv= [0, 1], представляющее лингвистическое значение истинности предпосылки «Пок1 естьP₁». Тогда «Пок1 естьP₁» есть«Пок1 естьD₁». По предпосылке правила «Пок1 естьP₁» и наблюдению «Пок1 естьD₁» определяется нечеткое множество степени истинности предпосылки. Определениеназывают определением обратного значения истинности, которое представляется формулой:

Нечеткое значение истинности заключения «∆uесть»выводится по степени истинностинечеткого условного предложения (продукционного правила)и нечеткому значению истинности предпосылки. С помощью логической системы Лукашевича можно представитькак:

Отсюда при заданных иможно определить. Обычнопредполагается истинным.

Далее по нечеткому значению истинности заключения «∆uесть» и нечеткому множеству заключенийможно определить нечеткое множествоC₁заключений «∆uестьC₁». Это называют определением значения истинности. Нечеткое множествоC₁определяется следующим выражением:.

Аналогично определяется , когда в нечетком косвенном выводе используется Правило 2.

При объединении Правила 1 и Правила 2 функция принадлежности C(∆u) определяется с помощью операции конъюнкции.

Далее для получения четкого значения изменения воздействующего фактора определяется значение ∆u^*, удовлетворяющее следующему выражению:, гдеU– полное множество выходных значений.

Рассмотрим определение обратного значения истинности в общем случае.

Пусть T– множество нечетких подмножествединичного интервала, представляющих лингвистические значения истинности, таких, что

,

где ↔ означает семантическую эквивалентность; X– переменная, принимающая значения в области определенияU;F– нечеткое подмножествоU;G– нечеткое подмножествоU, определенное следующим образом

 u  U

Здесь – нечеткое подмножествоV= [0, 1], представляющее лингвистическое значение истинности, аV– множество «численных» значений основной переменной ИСТИННОСТЬ.

Для решения обратной задачи определения истинности использовался принцип обобщения.

Пусть A– нечеткое подмножество области определенияUи пустьf– отображение изUв область определенияV. Принцип обобщения Заде утверждает, что образAподfявляется нечетким подмножествомV, определенным для всехvвVкак

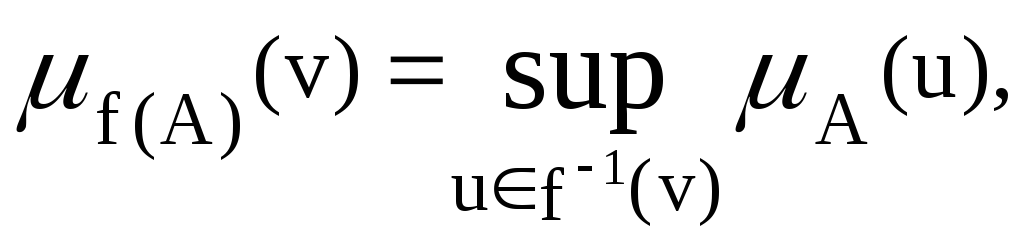
для

в противном случае.

В частном случае, когда _F– однозначное соответствие,

и однозначно определяется из знанияFиG.

В общем случае при решении обратной задачи определения истинности имеем множество Tнечетких подмножеств.₀и₁являются наименьшим и наибольшим элементомT, соответственно, и₀₁для всех членовT.

Для всех vв [0, 1]

для

и в противном случае.

для

и в противном случае.

Для всех uвU

.

₀и₁обеспечивают наилучшим образом нижнюю и верхнюю аппроксимацию для определения истинности, когда точное решение не может быть найдено.

Построение нечетких множеств ₀и₁ представлено на рис. 5.12 и 5.13.

v

F

G

 

τ₁

₁

1 ₀ 1 ₀

0

u

0

1

v

Рис. 5.12. Пример построения₀и₁

Рис.5.13.₀и₁из примера Рис.5.12.

В нечетких выводах измеренные данные наблюдения являются нечеткими из-за нечеткости измерений и интерпретации полученных значений.

Полагаем, что данное Dявляется нормальным нечетким множеством (SUP(D) = 1), имеющим симметричную треугольную функцию принадлежности, принимающую значения вокругd(Рис. 5.14).



1

D

0

d-k

d

d+k

U

Рис. 5.14. Представление нечеткого числа.

Использование нечетких исходных данных позволяет употребить несколько мер совместимости для сопоставления образов. В статье (Sanchez) предложены три меры совместимости: мера возможности, мера необходимости и показатель возможности-истинности в качестве оптимистической, пессимистической и нейтральной меры совместимости образа и данных, соответственно.

Пусть Pнечеткое подмножество образа области определенияU, аD– данное, выраженное нечетким числом. Тогда

мера возможности:

П (PD)=SUP (P  D) = SUP [  _P (u)   _D (u) ].

uU

мера необходимости:

N (PD)=INF (P  D’) = INF [  _P (u)   _D’ (u) ] ,

uU

где _P(u) и_D(u) значения функций принадлежности нечетких множествPиD.

Показатель возможности-истинности является дополнением к обычным мерам возможности и необходимости и основан на использовании лингвистической переменной ИСТИННОСТЬ, определении обратного значения истинности, применении принципа обобщения и уравнения нечеткого отношения.

Эта мера позволяет произвести сравнение данных с образом в терминах истинности. Она определяется из двух нечетких подмножеств единичного интервала ₀и₁, представляющих лингвистические значения истинности и дающих нижнюю и верхнюю аппроксимации оценки:

 (PD) = П ( ₀ ₁) =  _P (d).

N (PD)   (PD)  П (PD)

При нейтральном выборе (PD) нечеткость данных больше не рассматривается и нечеткое числоDзамещается числомd,(PD) =_P(d). Мера возможности наиболее употребляема, но имеет смысл при принятии решения учитывать все три меры.

На рис. 5.15 представлена оценка реакции показателя состояния организма по функциям принадлежности, построенным в соответствии с функцией Харрингтона, и с применением трех мер совместимости.

P– образ,D– данные: «вокруг»d

D^’ = 1 - D

D

D^’

хорошо P

2

3

1

Рис. 5.15. 1 – необходимость, 2 – возможность, 3 – показатель возможность-истинность

d

Объединение трех мер совместимости находит полезное практическое применение в выводах по правилам с И нечеткими суждениями в антецеденте. Так для показателей состояния испытуемого объекта можно определить класс реакции организма по совокупности показателей следующим образом. Медицинское знание представляется составными нечеткими суждениями

Класс А Если (Пок1 есть Р₁) И … И (ПокIесть Р_i)… И (ПокNесть Р_n).

Аналогично классу Aдля всех классов можно назначить оценки между 0 и 1, вытекающие из меры возможности, меры необходимости и показателя возможности-истинности.

Таким образом, связи между показателями и диагностическими группами выражаются посредством таблицы с показателями состояния в столбцах и классами реакции организма в строках.

При исследовании пациента получена следующая информация:

(Пок1 есть D₁) И … И (ПокIестьD_i)… И (ПокNестьD_n).

В n– мерном пространствеU=U₁´¼´U_n, для данного класса А

P=P₁´¼´P_nбудет определено как обычно:

для всех u= (u₁,¼,u_n)ÎU,m_P(u) =m_P1(u₁)Ù¼Ùm_Pn(u_n).

Аналогично для D=D₁´¼´D_n:

для всех u= (u₁,¼,u_n)ÎU,m_D(u) =m_D1(u₁)Ù¼Ùm_Dn(u_n).

Можно сравнить состояние пациента (D) с медицинским знанием (P) посредством меры возможности (П), меры необходимости (N) и показателя возможности-истинности (r).

П (PD) = П (P₁D₁)    П (P _nD_n) ,

N (PD) = N (P₁D₁)    N (P _nD_n),

 (PD) =  (P₁D₁)     (P _nD_n) =  _P1(d₁)     _Pn (d_N).

Сравнивая оценки классов, лежащие в диапазоне от 0 до 1, для всех трех мер, можно определить класс реакции объекта для оптимистических, пессимистических и нейтральных отношений.