Глава 3. Методы статистического анализа эксперимента.

Генеральная совокупность и случайная выборка.

На практике ис­следователь всегда располагает лишь ограниченным числом значений случайной величины, представляющим собой некоторую выборку из генеральной совокупности. Под генеральной совокупностью понимают все допустимые значения случайной величины. При анализе какой-либо технологической случайной величины, непрерывно изменяющейся по времени (например, температура, давление и т. п.), под наблюдаемыми значениями случайной величины понимают значения технологического параметра в дискретные моменты времени, разделенные таким интервалом, при котором соседние значения можно считать полученными из независимых опытов.

Выборка называется репрезентативной (представительной), если она дает достаточное представление об особенностях генеральной совокупности. Если о генеральной совокупности ничего не известно, единственной гарантией репрезентативности может служить случайный отбор. В очень многих исследованиях случайный отбор или случайное перемешивание (рандомизация) данных необходима. Для имитации случайного отбора можно использовать таблицы случайных чисел. Допустим, необходимо отобрать 10 элементов из совокупности, содержащей 100 элементов. Для этого надо пронумеровать элементы генеральной совокупности от 00 до 99. Затем, начиная с любого места таблиц, выписать две последние цифры десяти идущих подряд чисел. Например, начиная с первого числа, получились номера

82 49 18 48 09 50 17 10 37 51

(если числа повторяются, их надо опустить). Полученные номера показывают, какие элементы надо отобрать. Выбранную последовательность изменять нельзя. Нарушение случайности, как правило, ведет к искажению результатов. Аналогично отбору производится рандомизация элементов. При этом нужно выписывать случайные номера до тех пор, пока они не охватят все заданные элементы.

Из случайного характера выборок немедленно вытекает, что любое суждение о генеральной совокупности по выборке само случайно. Предположим, что в результате эксперимента получена выборка y₁,y₂, …,y_nзначений случайной величиныY. Пустьy— некоторая точка числовой оси х; обозначим черезnчисло выборочных значений, расположенных левееyна той же оси. Отношениеn_y/nпредставляет собой частоту полученных в выборке значений случайной величиныY, меньшихy. Эта частота есть функция отy. Обозначим ееF_n(y):

Функция распределения F_n(y), получаемая по выборке, называется эмпирической иливыборочной функцией распределения(в отличие от распределения генеральной совокупности, или теоретического распределения). Для каждой выборки эмпирическая функция распределения будет своей, но все эмпирические функции распределения одной и случайной величины будут иметь нечто общее, что является информацией о функции распределения этой случайной величины.

Можно доказать (теорема Гливенко), что с вероятностью 1 при максимальная разность между функциями распределения случайных величинF_n(y) иF(y) стремится к 0. Практически это означает, что при достаточно большой выборке функцию распределения генеральной совокупности приближенно можно заменять выборочной функцией распределения.

При обработке выборок больших объемов используют метод «сгруппированных данных»: выборка объема nпреобразуется в статистический ряд. Для этого весь диапазон изменения случайной величины в выборке:делится наkравных интервалов. Число интервалов можно выбирать по формуле:, с округлением до ближайшего целого. Длина интервалаhравна . Число элементов выборки, попавших вi-й интервал, обозначим черезn_i. Величина, равная, определяет относительную частоту попадания случайной величины в i-й интервал. Все точки, попавшие вi-й интервал, относят к его середине:

Статистический ряд записывается в виде табл. 3.1.

Таблица 3.1.

Статистический ряд

Интервал	Длина интервала	Середина интервала	Число точек в интервале	Относительная частота
1	(ymin,y1)		n1
2	(y1, y2)		n2
, , ,	, , ,	, , ,	, , ,	, , ,
i	(yi-1, yi)		ni
, , ,		, , ,	, , ,	, , ,
k	(yk-1, yk)		nk
∑			n	1

График, который можно построить по данным табл. 3.1, называется гистограммой эмпирического или выборочного распределения.

При обработке наблюдений обычно не удается получить эмпирическую функцию распределения. Даже простейший анализ условий проведения опытов позволяет с достаточной степенью уверенности определять тип неизвестной функции распределения. Окончательное уточнение неизвестной функции распределения сводится к определению некоторых числовых параметров распределения. По выборке могут быть рассчитаны статистические характеристики (выборочное среднее, дисперсия и т.д.), которые являются оценками соответствующих генеральных параметров. Оценки, получаемые по выборке, сами являются величинами случайными, но нужная точность при этом достигается при меньших n, чем при непосредственном использовании теоремы Гливенко. К оценкам обычно предъявляются требования состоятельности и несмещенности. Оценканазывается состоятельной, если с увеличением объема выборкиnона стремится (по вероятности) к оцениваемому параметруa. Эмпирические (выборочные) моменты являются состоятельными оценками теоретических моментов. Оценка называется несмещенной, если ее математическое ожидание при любом объеме выборки равно оцениваемому параметру. Еще одной важной характеристикой оценок генеральных параметров является их эффективность, которая для различных несмещенных оценок одного и того же параметра при фиксированном объеме выборок обратно пропорциональна дисперсиям этих оценок.

Метод максимального правдоподобия.

Для получения оценок используют различные методы. Широко применяется метод максимального правдоподобия. Оценки, полученные при помощи этого метода, отвечают большинству изложенных требований. Сущность метода максимального правдоподобия заключается в нахождении таких оценок неизвестных параметров, для которых функция правдоподобия при случайной выборке объема nбудет иметь максимальное значение. Пусть известен общий вид плотности вероятностиf(y,а) теоретического распределения; а — неизвестный параметр, входящий в выражение закона распределения. На опыте получена выборка значений случайной вели­чиныy₁,y₂, ...,y_n. Окружим каждую точку х_i, окрестностью длины ε. Вероятность попасть в интервал с границамиприближенно равнаf(y_i,a)ε. Если произведеноnнаблюдений, то ве­роятность того, что одновременно первое наблюдение попадает в пер­вый интервал, второе — во второй и т. д., есть вероятность совмест­ного осуществления событий и в силу независимости событий равна произведению вероятностей:

Событие с вероятностью Росуществилось на самом деле. Естественно ожидать, что событию, осуществившемуся при первом же испытании, со­ответствует максимальная вероятность. Поэтому в качестве оценки для а следует взять то значениеа*из области допустимых значений параметраа, для которого эта вероятность принимает наибольшее воз­можное значение, т.е. корень уравнения

представляющего собой необходимое условие экстремума вероят­ности Р. Достаточным условием максимума при этом является выпол­нение неравенства. Если максимумов несколько, необходимо выбрать среди них наиболь­ший. Решение проще получить, если перейти к функции , которая называется функцией правдоподобия. ВероятностьРи функ­цияLимеют максимумы при одних и тех же значениях определяемых параметров, так как .

В общем случае требуется оценить одновременно несколько пара­метров одномерного или многомерного распределения. Если а иyпонимать как векторы, то формулировка принципа максимального правдоподобия сохранится: надо найти такую совокупность допустимых значений параметровкоторая обращает функцию правдоподобия в максимум. Необходимые условия экстремума дает система уравнений

а неотрицательная определенность матрицы

является достаточным условием того, чтобы локальный экстремум был максимумом функции правдоподобия.

Оценка математического ожидания и дисперсии.

Метод максималь­ного правдоподобия всегда приводит к состоятельным, хотя иногда и смещенным оценкам, имеющим наименьшую возможную дисперсию при неограниченном возрастании объема выборки. Для нормально распределенной случайной величины получают оценки следующего вида: среднее арифметическое для математического ожиданияm_y

и выборочную дисперсию для дисперсииD[Y]

Последняя оценка получается несколько смещенной:

Для получения несмещенной оценки надо умножить на n/(n-1):

Уменьшение знаменателя на единицу непосредственно связано с тем, что величина , относительно которой берутся отклонения, сама зависит от элементов выборки. Каждая величина, зависящая от элементов выборки и входящая в формулу выборочной дисперсии, называетсясвязью.

Классификация ошибок измерения.

Каждый результат измерения — случайная величина. Отклонение реального результата от истинного называется ошибкой наблюдения. Ошибка наблюдения также есть слу­чайная величина — она является результатом действия только случайных (не учитываемых) факторов. Если обозначить истинный результат через а, ошибку — через ∆Y, результат измерения — черезY, то

Y-а= ∆Y.

Различают ошибки трех видов.

1. Грубые ошибкивозникают вследствие нарушения основных усло­вий измерения. Результат, содержащий грубую ошибку, резко отличает­ся по величине от остальных измерений. На этом основаны некоторые критерии исключения грубых ошибок.

2. Систематические ошибкипостоянны во всей серии измерений или изменяются по определенному закону. Выявление их требует спе­циальных исследований, но как только систематические ошибки обна­ружены, они могут быть легко устранены введением соответствующих поправок в результаты измерения.

3. Случайные ошибки— ошибки измерения, остающиеся после устране­ния всех выявленных грубых и систематических ошибок. При таком определении к случайным факторам, порождающим случайную ошибку, не относят факторы с постоянным действием (систематические ошиб­ки) и факторы с однократным, но очень сильным действием (грубые ошибки). Случайные ошибки вызываются большим количеством таких факторов, эффекты действия которых столь незначительны, что их нельзя выделить в отдельности (при данном уровне техники измерения). При этом распределение случайных ошибок симметрично относительно нуля; ошибки, противоположные по знаку, но равные по абсолютной величине, встречаются одинаково часто. Из симметрии распределения ошибок сле­дует, что истинный результат наблюдения есть математическое ожидание соответствующей случайной величины. Так как изY =а+ ∆Yи при отсутствии грубых и систематических ошибок

M[∆Y]=0

то

M[Y]=a

В дальнейшем будут рассматриваться только случайные ошибки измере­ний.

Закон сложения ошибок.

Для независимых случайных величин свойством аддитивности обладают дисперсии, а не среднеквадратичные ошибки. Если Y₁, Y₂, …, Y_n — независимые случайные величины;a₁,a₂, …,a_n— неслучайные величины и

то выборочная дисперсия величины Zопределяется следующим образом:

.

Если положить a₁=a₂=…=a_n=1/n, то

В этом случае

где

Если величины Y₁,Y₂, …,Y_nинтерпретировать какnнезависимых наблюдений одной и той же случайной величиныY, то.

Тогда получим

(3.1)

Из выражения (3.1) следует практический вывод: при оценке двух методов следует учитывать длительность анализа. Применяя менее точный экспресс-метод, можно сделать за то же время значительно большее число опытов и добиться более высокой точности, чем дает трудоемкий точный метод.

Ошибки косвенных измерений.

Измерения делятся на прямыеикосвенные. В первом случае непосредственно измеряется определяемая величина, при косвенных измерениях она задается некоторой функцией от непосредственно измеряемых величин. Пусть случайная величинаzзависит от наблюденийz, зависит от наблюденийy₁, y₂, …,y_nпо известному закону;

Истинное значение величины zможет не совпадать с математическим ожиданиемМ_z, а определяться тем же законом:

Величина a_zназывается средним косвенного измерения.

Дисперсия косвенного измерения определяется так же, как обычная дисперсия, только отклонения берутся от среднего косвенного измеренияa_z. Ее можно найти, зная дисперсии отдельных наблюдений и вид функцииf. На практике определяют выборочные дисперсиии по ним выборочную дисперсию косвенного измерения, которая служит оценкой генеральной дисперсии. Чтобы найти, разложим функцию в ряд Тейлора в точке, ограничиваясь членами первого порядка

(3.2)

и определим по закону сложения дисперсий

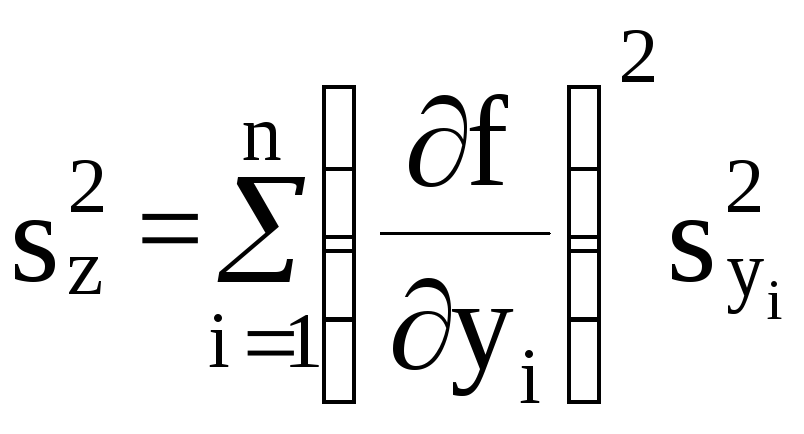. (3.3)

Выражение (3.3) называют закономнакопления ошибок.

Определение дисперсии по текущим измерениям.

Математическое ожидание (среднее) и дисперсия генеральной совокупности оцениваются средним и дисперсией выборки тем точнее, чем больше объем выборки. При этом среднее характеризует результат измерений, а дисперсия — точность этого результата (дисперсия воспроизводимости). Если проделаноmпараллельных опытов (опытов, проведенных при неизменном комплексе основных факторов) и получена выборкаy₁,y₂, …,y_mзначений измеряемой величины, то дисперсия воспроизводи­мости равна

и ошибка опыта (ошибка воспроизводимости)

Часто для оценки точности применяемой методики ставят специальную серию опытов, многократно повторяя анализ одной и той же пробы. Haпроведение большой серии опытов требуется много времени, в течение которого может неконтролируемым образом измениться среднее значение результатов анализа. Значительно проще и удобнее определять ошибку воспроизводимости по текущим измерениям. Предположим, анализируютсяnпроб. При анализе каждой пробы делается различное число параллельных опытов:m₁,m₂, …,m_n. Вычис­лим частные дисперсиидля каждой такой выборки в отдельности. Число степеней свободы частных дисперсий соответственно

равно: . Общая дисперсия воспроизводимости всех опытов будет равна средневзвешенному значению частных дисперсий (в качестве весов берутся степени свободы):

(3.4)

Число степеней свободы общей дисперсии равно общему числу измерений минус число связей, использованных для определения nсредних:

(3.5)

Учитывая, что частные дисперсии определяются по результатам параллельных опытов по формуле:

тогда из (3.4) имеем

(3.6)

Если число параллельных опытов при анализе каждой пробы одинаково m₁ =m₂= … =m_n=m, формулы для расчета дисперсии воспроизводимости упрощаются. При этом

(3.7)

Таким образом, при равном числе параллельных опытов общая дисперсия воспроизводимости равна среднеарифметическому значению частных дисперсий. Число степеней свободы общей дисперсии при этом равно

(3.8)

И тогда

(3.9)

Число степеней свободы у общей дисперсии воспроизводимости, определяемой по формулам (3.6) и (3.9), гораздо больше, чем у каждой частной дисперсии в отдельности. Поэтому общая дисперсия воспроиз­водимости намного точнее оценивает дисперсию генеральной совокупности .

При вычислении дисперсии воспроизводимости по текущим измерениям объединяют между собой только те пробы, которые можно рассматривать как выборки из генеральных совокупностей с равными дисперсиями. При этом каждое из значений можно рас­сматривать как оценку одной и той же генеральной дисперсии.

Проверка статистических гипотез.

Под статистическими гипотезамипони­маются некоторые предположения от­носительно распределений генеральной совокупности той или иной случайной величины. Проверка гипотезы заключа­ется в сопоставлении некоторых стати­стических показателей,критериев про­верки (критериев значимости), вычисляе­мых по выборке, со значениями этих показателей, определенными в пред­положении, что проверяемая гипотеза верна. При проверке гипотез подвергает­ся испытанию некоторая гипотезаH₀ в сравнении сальтернативной гипотезой H, которая формулируется или под­разумевается. Альтернативных гипотез может быть несколько. Чтобы принять или отвергнуть гипотезу, еще до получения выборки задаются уровнем значимостир. Наиболее употребительны уровни значи­мости 0,05; 0,02; 0,01; 0,10; 0,001. Уровню значимости соответствует довери­тельная вероятность= 1 - р. По этой вероятности, используя гипотезу о распределении оценки* (критерия значимости), находят квантильные доверительные границы, как правило, симметричные_p/2и_1-p/2. Числа_p/2и_1-p/2называютсякритическими значениями гипотезы; зна­чения*, меньшие_p/2и большие_1-p/2, образуют критическую область гипотезы, или область непринятия гипотезы. Если найденное по выборке значение₀попадает между_p/2и_1-p/2, то гипотеза допускает такое значение в качестве случайного, и поэтому нет оснований ее отвергать. Если же найденное значение₀попадает в критическую область, то по данной гипотезе оно является практически невозможным. Но так как оно все-таки появилось, то отвергается гипотеза.

При проверке гипотез можно совершать ошибки двух типов. Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероятность такой ошибки не больше принятого уровня значимости. Например, при р=0,05 можно совершить ошибку первого рода в пяти случаях из ста. Ошибка второго рода состоит в том, что гипотеза принимает­ся, а на самом деле она неверна. Вероятность ошибки второго рода зависит от характера проверяемой гипотезы, от способов проверки и от многих других причин, что сильно усложняет ее оценку.

Эта вероятность тем меньше, чем выше уровень значимости, так как при этом увеличивается число отвергаемых гипотез. Одну и ту же статисти­ческую гипотезу можно исследовать при помощи различных критериев значимости. Если вероятность ошибки второго рода равна , то 1 —называют мощностью критерия. На рис. 16 приведены две кривые плот­ности вероятности случайной величины, соответствующие двум конку­рирующим гипотезам Н(а) и(б).

Если из опыта получается значение >_p, отвергается гипотезаHи принимается альтернативная гипотеза, и наоборот, если<_p. Площадь под кривой плотности вероятности, соответствующей справедливости гипотезыHвправо от_p, равна уровню значимостиp, т.е. вероятности ошибки первого рода. Площадь под кривой вероятности, соответствующей справедливостивлево от_pравна вероятности ошибки второго рода, а вправо от_p– мощности критерия. Таким образом, чем большеpтем больше 1 -. Для проверки гипотезы стремятся из всех возможных критериев выбрать тот, у которого при заданном уровне значимости меньше вероятности ошибки второго рода.

Оценка математического ожидания нормально распределенной случайной величины.

При отсутствии грубых и систематических ошибок математическое ожидание случайной величины совпадает с истинным результатом наблюдений. Поэтому оценка математического ожидания имеет важное значение при обработке наблюдений. Легче всего оценить математическое ожидание при известной дисперсии генеральной совокупности. генеральную дисперсию s²нельзя получить из наблюдений, а только оценить при помощи выборочной дисперсии. Ошибка от замены генеральной дисперсии выборочной будет тем меньше, чем больше объем выборкиn. На практике эту погрешность не учитывают приn50. В дальнейшем предполагается, что наблюдаемая случайная величина имеет нормальной распределение.

При небольших объемах выборок для построения доверительного интервала математического ожидания используют распределение Стьюдента, или t-распределение. Распределение Стьюдента имеет случайная величинаt:

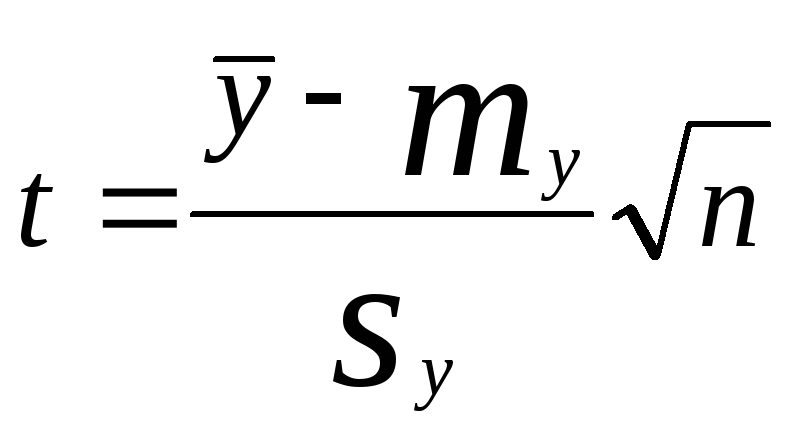(3.10)

Плотность ее вероятности имеет следующий вид:

(3.11)

где Г(f) – гамма-функция;f– число степеней свободы выборки.

Если дисперсия и среднееопределяются по одной и той же выборке, тоf=n-1.

Таким образом, распределение Стьюдента зависит только от числа степеней свободы f, с котором была определена выборочная дисперсия. Так как распределение Стьюдента симметрично относительно 0, то зачастую пользуются обозначениемt_p,f, гдеf– число степеней свободы, аp– вероятность, с которой рассматривается процесс.

Оценка дисперсии нормально распределенной случайной величины.

Дисперсию генеральной совокупности нормально распределенной случайной величины можно оценить, если известно распределение ее оценки — выборочной дисперсии. Распределение выборочной диспер­сии можно получить при помощи распределения Пирсона или²-распределения. Если имеется выборкаnнезависимых наблюденийy₁,y₂, …,y_nнад нормально распределенной случайной величиной, то сумма

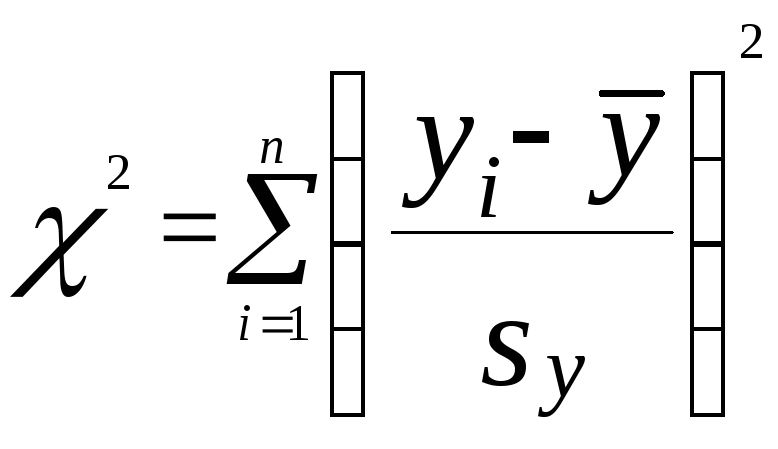(3.12)

имеет распределение ²сf=n-1 степенями свободы.

Плотность ²распределения зависит только от числа степеней свободыf:

0²<(3.13)

где Г(f) – гамма-функция.