5.1.2. Термодинамика упругого деформирования

Рассмотрим энергетические соотношения при упругой деформации породы. Для работы напряжений (объемных внутренних сил) по изменению тензора деформаций получим

. (5.4)

Поясним формулу (5.4). Элементарная работа объемных внутренних сил для смещения - (напомним, что - , , , ) - . Представляя интеграл по объему от - в виде суммы интегралов по поверхности и объему - (интегрирование по частям), заметим, что в пределе - интеграл по поверхности обращается в нуль (неограниченную среду на бесконечности можно считать недеформированной). Учитывая симметричность тензора деформаций, второй интеграл представим в виде - . Откуда следует справедливость (5.4) при переходе к пределу - .

Используя первое начало термодинамики, запишем

, или (5.5)

где , - изменение, соответственно, внутренней и свободной энергии деформируемой породы; - температура; - энтропия. Считая процесс адиабатическим ( ) или изотермическим ( ), получим

. (5.6)

Коэффициенты можно определить через внутреннюю или свободную энергию, используя (5.1)

. (5.7)

Учитывая, что вторая частная производная не зависит от порядка дифференцирования, приходим к равенству упругих модулей относительно перестановки первой и второй пар индексов, т.е. (или в матричном виде - ). В силу линейности закона Гука можно прейти к аналогичному выводу относительно модулей податливости, т.е. (или в матричном виде - ). Легко подсчитать количество независимых модулей, обратив внимание, что квадратные матрицы в (5.3) являются симметричными. Получим 6 + 5 + 4 + 3 + 2 + 1 = 21 независимый модуль.

5.1.3. Использование свойств симметрии для определения количества модулей упругости (на примере минералов кубической системы)

Оказывается, что для различных минералов количество независимых модулей зависит от симметрии внутреннего строения минералов подобно тому, как симметрия тензоров напряжения и деформации приводит к уменьшению количества независимых модулей. Симметрия минералов предполагает существование упорядоченной структуры минерала, т.е. кристаллической решетки. Характеристики симметрии кристалла заключаются в установлении следующих преобразований: поворотов, отражений, комбинаций поворотов и отражений и т.д. При установленных преобразованиях симметрии кристаллическая решетка минерала совмещается сама с собой.

П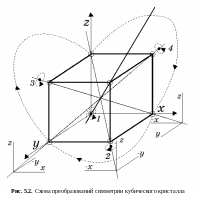 редположим, что кристаллическая решетка может быть составлена кубами без зазоров, а в пересечениях ребер кубов находятся атомы одного сорта. При повороте куба вокруг собственной пространственной диагонали на углы 120⁰, 240⁰, 360⁰ каждый атом будет совмещаться со своим соседом (рис. 5.2). При этом кристалл будет оставаться неизменным. Таким образом, кристаллическая решетка минерала обладает осью 3-го порядка.

Очевидно, что количество преобразований симметрии ограничено. Подсчетом общего количества преобразований симметрии заниматься не будем. Отметим лишь, что существует 7 кристаллографических систем: триклинная, моноклинная, орторомбическая, кубическая, тетрагональная, тригональная и гексагональная. Наибольшей симметрией обладает кубическая система. Так, к кубической системе относятся кристаллические решетки алмаза, сфалерита, галита и др. Более подробное изложение вопроса можно найти в учебниках по кристаллографии, например [26].

Для установления связи между симметрией кристалла и количеством независимых модулей упругости запишем выражение для свободной энергии упругодеформированного минерала, приходящейся на единицу объема. Используя закон Гука в тензорном виде, получим

. (5.8)

Поскольку при преобразованиях симметрии кристалл остается неизменным, то должна оставаться неизменной и свободная энергия упругодеформированного кристалла.

Определим количество независимых модулей упругости для минерала, относящегося к кубической системе. Для этого выберем прямоугольную систему координат так, чтобы координатные оси составляли одинаковые углы с осью симметрии 3-го порядка, проходящей через начало координат (рис. 5.2). Поскольку ось 3-го порядка совпадает по направлению с пространственной диагональю куба, то таких осей будет четыре. Поэтому необходимо рассмотреть четыре преобразования системы координат. В соответствии со схемой преобразования, приведенной на рис. 5.2 получим следующие условия

. (5.9)

Согласно формуле (5.8) необходимо рассмотреть произведения - ( ) и оставить те, которые при преобразованиях переходят друг в друга без изменения знака. Для этого необходимо учесть, что при изменении направления координатной оси на противоположное имеет место равенство - . Например, для - при - изменяется знак в знаменателе не только первого слагаемого, но и знак в числителе второго слагаемого, так как - смещение вдоль оси - . Легко убедиться, что указанным требованиям удовлетворяют только суммы вида¹⁾: (согласно первому условию (5.9): - равенство сумм слева и справа очевидно; рассматривая оставшиеся условия, прейдем к аналогичному выводу); ; . Рассматривая первую сумму, находим, что - , аналогично для второй суммы - и третьей суммы - . Таким образом, количество независимых упругих модулей для минералов, относящихся к кубической системе, равно трем. Поэтому закон Гука в этом случае принимает вид

. (5.10)

Выражение для свободной энергии упругодеформированного минерала, относящегося к кубической системе, в развернутом виде запишется следующим образом

. (5.11)

Наличие множителя «2» перед третьей скобкой объясняется тем, что через параметр « » обозначаются четыре упругих модуля.

Сравнительно простой вид уравнений (5.10) и (5.11) получается лишь при выборе системы координат с осями, проходящими вдоль ребер куба. При произвольном выборе системы координат количество модулей упругости, отличных от нуля, будет по-прежнему равно 21.

В отличие от минералов горные породы, которые можно было бы отнести к кубической системе, не обладают кубической симметрией в буквальном смысле. Однако в первом приближении такие породы могут быть представлены в виде сфер или «макроатомов», упакованных в виде кубов. В качестве примера приведем хорошо отсортированные зернистые породы. Очевидно, что закон Гука (5.10) также справедлив в этом случае.