5.2. Закон Гука для изотропных пород
Оказывается, что закон Гука для изотропных горных пород (пород, обладающих высшей симметрией) может быть получен как частный случай закона Гука для минералов, относящихся к кубической системе. Действительно, если для упругих модулей таких минералов выполняется условие
, (5.12)
то с учетом выражений
для инвариантов тензора деформаций
(4.49) выражение для свободной энергии
(5.11), представленное через пары модулей,
например, -
и
,
приобретает вид
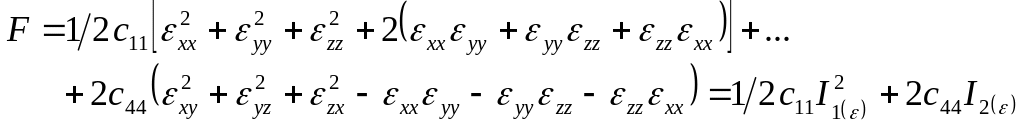; (5.13)
,
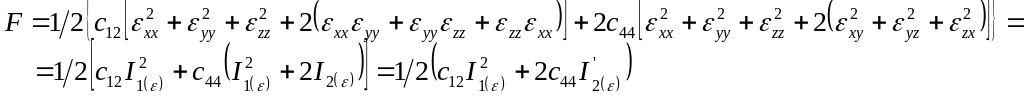(5.14)
где
- второй инвариант тензора деформаций
по аналогии с -
(§4.3).
Условие
(5.12) еще называют условием изотропии
кристалла, обладающего кубической
симметрией. В то же время в кристаллографии
величину -
,
определяемую
при одноосной
деформации, принято называть модулем
Юнга по
аналогии с коэффициентом пропорциональности
в законе Гука для изотропного стержня.
Действительно, если коэффициент -
не зависит от
преобразований системы координат, то
он в точности соответствует модулю Юнга
для изотропного тела. Используя закон
преобразования тензора 4-го ранга при
переходе от одной (нештрихованной)
системы координат к другой (штрихованной)
системе -
,
где
-
направляющие косинусы между координатными
осями штрихованной и нештрихованной
систем координат, для модуля Юнга
кристалла получим
.
Используя тождество
и переходя к
матричным обозначениям упругих модулей,
окончательно получим
.
Из требования инвариантности преобразований
-
следует условие (49).
Выражения (5.13) и (5.14) имеет простой физический смысл. Свободная энергия упругодеформированного изотропного минерала, будучи функцией от суммы квадратов деформаций, может быть выражена через два независимых инварианта тензора деформаций или комбинацию двух независимых инвариантов. Поскольку свободная энергия (как и инварианты тензора деформации, и их комбинации) не зависит от выбора системы координат, то не зависят от выбора системы координат и упругие модули, входящие в выражение для свободной энергии.
Для изотропных твердых тел выражение (5.14) принято записывать в следующем виде
, (5.15)
где
,
,
.
Величины -
и
называются коэффициентами Ламе.
В развернутом виде системы уравнений (5.3), составляющие закон Гука, в случае изотропных пород примут следующий вид:
; (5.16)
. (5.17)
Выясним,
какие ограничения накладываются на
коэффициенты Ламе. Состоянию
термодинамического равновесия отвечает
минимум свободной энергии, соответствующий
-
при -
,
следовательно,
.
Поэтому свободная энергия является
положительно определенной квадратичной
формой от деформаций. Приведенное
неравенство составляет условие
устойчивости деформируемого тела.
Из теории квадратичных
форм известно, что квадратичная форма
будет положительной, если будут
положительны все главные миноры
квадратной матрицы коэффициентов формы.
В нашем случае необходимо рассмотреть
миноры квадратной матрицы в (5.16). Первый
минор этой матрицы -
,
второй минор -
,
третий
минор –
.
Последующие миноры отличаются от
третьего минора лишь степенью коэффициента
-
.
Анализируя условия -
,
и
,
приходим к выводу, что коэффициенты
Ламе должны удовлетворять следующим
требованиям
и
. (5.18)
В соответствии с проведенным анализом обобщенного закона Гука можно утверждать, что для кристаллических тел изотропия является частным случаем кубической симметрии. На самом деле горные породы представлены минералами, относящимися к различным системам симметрии, и должны обладать существенной анизотропией. Поэтому, казалось бы, уравнения (5.16)-(5.17) не применимы для описания упругих свойств реальных горных пород. Если рассматривать сравнительно малые объемы горных пород, соизмеримые с объемами минеральных включений, то это действительно так. Однако в ряде случаев породы могут считаться изотропными телами, когда в деформируемом блоке преимущественная ориентация минеральных зерен, элементов порового пространства не устанавливается для какого-либо направления, т.е. носит статистический характер. Ограниченность применимости уравнений (5.16)-(5.17) иногда выявляется для сравнительно больших объемов горных пород – массивов. Это связано со слоистостью, блочностью, неоднородностью массива или его частей. Поэтому для корректного решения задач по определению напряженно-деформированного состояния массива, образца породы необходимо обосновать принадлежность объекта к той или иной системе симметрии. Выраженная слоистость, упорядоченная блочность являются надежными признаками, чтобы считать породу анизотропной.