5.2.2. Связь между пористостью и модулем Юнга

Выше уже говорилось, что одной из отличительных особенностей горных пород является наличие в них порового пространства. Этот факт являлся главенствующим в обсуждении плотностных и фильтрующих свойств горных пород. Следует ожидать, что между пористостью породы и ее упругими модулями будет существовать определенная связь. Однако нельзя найти однозначной связи такого влияния, используя только параметр пористости и модули упругости для минеральной фазы породы. Еще требуются определенные предположения относительно структуры порового пространства, например, о виде пор (сфера, вытянутая пора типа трещины), о систематизации пор (системы трещин, капилляров или поры ориентированы беспорядочно). Только в этом случае можно строить модели, объясняющие количественные связи между различными характеристиками горной породы. Очевидно, что на адекватность модели будет оказывать степень неоднородности породы.

Рассмотрим простейшую модель породы, имеющей общую пористость - и модуль Юнга минерального скелета - . Поровое пространство представим в виде ориентированных в одном направлении и не смыкающихся при деформации прямолинейных трубок. Определим модуль Юнга породы - . После очевидных преобразований получим следующий результат

или , (5.28)

где - сила, действующая вдоль направления трубок; - относительная деформация; и - суммарные площади поперечных сечений минерального скелета и трубок соответственно; - размер образца вдоль направления действия силы. Даже такая грубая модель позволяет предсказать зависимость модуля Юнга изотропной горной породы от пористости (не будем учитывать очевидную анизотропию порового пространства).

Модель (5.28) можно уточнить следующим образом. Предположим, что происходит смыкание отдельных пор при деформации. Тогда смыкание пор приведет к увеличению площади - по сравнению с . В результате следует ожидать, что кривая зависимости - в реальном случае пойдет выше линейной зависимости (5.28) и будет носить, например, квадратичный характер, что оправданно для линейного уменьшения просвета пор. Путем введения коэффициента при - учтем форму порового пространства – характеристику отклонения реальной формы пор от формы трубок. Тогда можно предложить формулу для аппроксимации экспериментальных данных модуля Юнга для различных значений общей пористости в виде

. (5.29)

Формула (5.29) предложена в [33], в которой - подгоночный параметр формы порового пространства ( ). Значение подгоночного параметра определяется таким образом, чтобы получить минимальное значение для среднеквадратичного отклонения экспериментальных данных от результатов, следующих из аппроксимируемой формулы.

5.2.3. Работа деформирования упруго-пластичных изотропных пород

Для идеально упругой изотропной породы выражение для работы внешних сил по ее деформированию, приходящейся на единицу объема, (удельной работы) согласно выражению (5.8) и закону Гука (5.24) будет

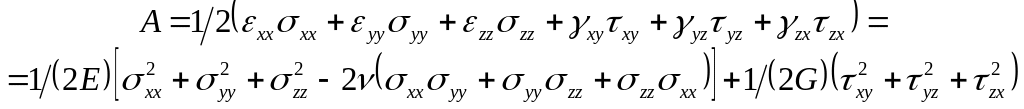. (5.30)

Размерность удельной работы - .

При одноосном приложении нагрузки, например, вдоль оси - выражение (5.30) для работы упругого деформирования приобретет наиболее простой вид

. (5.31)

Практический интерес представляет не сама работа деформирования, а энергия, необходимая для разрушения единицы объема породы (удельная энергия разрушения). В этом случае в выражении (5.31) необходимо заменить значение текущего напряжения - на некоторое предельное значение - , при котором происходит разрушение породы (глава 6). Для определенности положим - , где - предел прочности при одноосном сжатии.

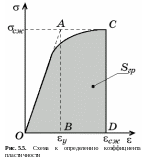Рассмотрим удельную энергию разрушения упруго-пластичной породы. Очевидно, что удельной энергии разрушения соответствует площадь под графиком деформация – напряжение (рис. 5.5). Не будет грубой ошибкой, если аппроксимировать площадь под графиком в виде суммы площадей треугольника и прямоугольника с одинаковыми сторонами, равными - . Выясним физический смысл площадей указанных фигур. Площадь треугольника будет численно равна удельной энергии разрушения абсолютно упругой породы с пределом прочности - . В то же время площадь прямоугольника будет соответствовать дополнительной удельной энергии, необходимой для достижения предельных пластических деформаций для разрушения упруго-пластичной породы с тем же пределом прочности.

Для того чтобы сопоставлять энергии разрушения различных пород, имеющих одинаковый предел прочности при сжатии, удобно ввести параметр – коэффициент пластичности. Коэффициент пластичности определяется через отношение энергии разрушения упруго-пластичной породы к энергии разрушения упругой породы для одного и того же значения предела прочности. Согласно обозначениям, приведенным на рис. 5.5, для коэффициента пластичности получим

. (5.32)

Если ввести следующие модули: - модуль полной деформации упруго-пластичной породы и - - модуль Юнга упругой породы, то с учетом (5.32) выражение для коэффициента пластичности примет следующий вид

. (5.33)

Поскольку - , то минимальное значение для коэффициента пластичности - будет для упругой породы. Для упруго-пластичной породы - . Таким образом, минимальная энергия разрушения требуется для разрушения упругих пород, которые обладают наименьшими предельными деформациями. По характеру разрушения такие породы называются хрупкими породами. Поэтому иногда удобно пользоваться величиной, равной отношению работы деформирования породы на линейном участке к энергии разрушения породы. Эту величину предложил Л.И. Барон и назвал ее коэффициентом хрупкости. В первом приближении можно считать, коэффициент хрупкости обратно пропорционален коэффициенту пластичности, т.е. . Очевидно, что справедливо - .

Наибольшей пластичностью обладают связные породы с преобладанием глинистых минералов. В то же время наиболее хрупкими являются малопористые изверженные нерудные породы.