5.3.2. Усреднение упругих модулей (на примере трансверсально-изотропной среды)

Опытное получение модулей - , , , , , входящих в уравнения (5.34), представляется крайне затруднительным. Это связано с тем, что для их определения требуются образцы горной породы, включающие слои количеством, зависящим от степени неоднородности, минералогического состава и структуры породы, разброса толщин слоев. При этом необходимое количество слоев, которое позволяет судить о представительности образца, может достигать десятков и более. В результате образец может иметь размеры, соизмеримые с размерами горной выработки, что практически не позволяет создать условия для инструментального определения модулей.

Решение рассматриваемой проблемы может осуществляться разными путями. Один из путей заключается в подборе комбинации модулей - , , , , , обеспечивающей наилучшее согласие между напряженным и деформированным состояниями, характеристики которых могут быть определены в результате натурных измерений или измерений на моделях. Поэтому получаемые таким образом значения модулей являются подгоночными параметрами. При этом существует ряд недостатков. С одной стороны инструментальные измерения, как правило, проводятся для узких интервалов изменений деформаций и напряжений, нежели для интервалов, имеющих место в реальных условиях. С другой стороны большое количество подгоночных параметров приводит к неоднозначному выбору подходящей их комбинации.

Однако можно пойти и другим путем: провести усреднение упругих модулей, характеризующих отдельные слои. Основная идея усреднения заключается в замене упругих модулей каждого слоя некоторой эффективной величиной, определяемой, как правило, вдоль или вкрест слоистости породы с учетом мощности слоев. В этом случае, упругие модули в системе уравнений (5.34) будут представлять собой средние значения упругих параметров всех слоев. Процедура усреднения хорошо сочетается с обработкой результатов лабораторных исследований выборки образцов, отобранных из разных слоев массива.

Рассмотрим закон Гука в виде первой системы уравнений (5.3). Вид матрицы упругих модулей для трансверсально-изотропной среды будет соответствовать виду матрицы упругих модулей для среды с кубической симметрией (5.10). В этом можно убедиться, используя результаты предыдущего параграфа. Однако в матрице упругих модулей трансверсально-изотропной среды будет пять независимых величин - . Остальные модули выражаются следующим образом: , , , . Переходя от матричного вида закона Гука к его явному виду, получим следующую систему уравнений

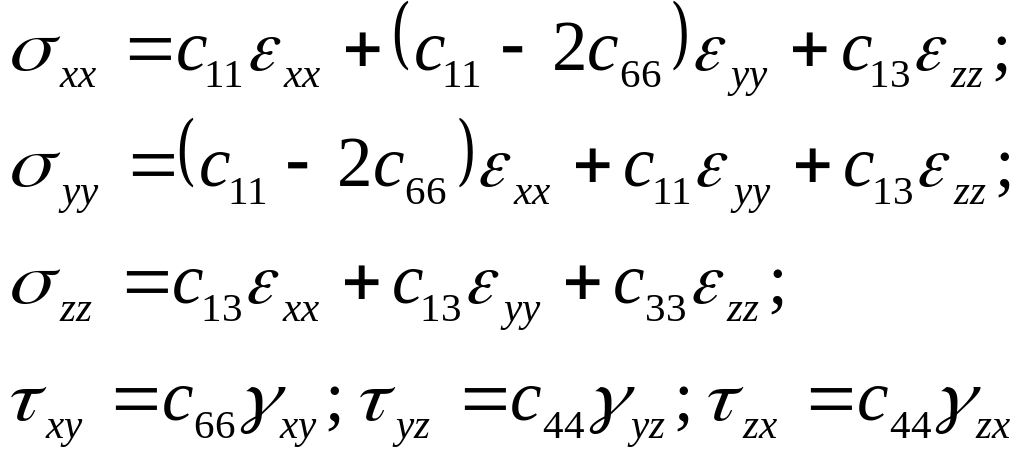. (5.36)

В качества примера покажем, как вычисляются средние значения модулей упругости для нормальных деформаций поперек и вдоль слоев - , . Для простоты будем считать горную породу, состоящую из слоев двух типов с упругими модулями, выраженными через коэффициенты Ламе - , и , и относительной мощностью слоев каждого типа - и ( , где , , - соответственно, суммарные толщины слоев первого типа, слоев второго типа и толщина породы). Поскольку при усреднении параметров в данном направлении подразумевается замена среды с чередованием слоев эффективной изотропной средой, то обоснованно воспользоваться законом Гука в виде (5.16).

Модуль упругости - определяется из 3-го уравнения системы (5.36) при условии равенства нулю деформаций - и по формуле - . Для сплошной среды на каждый слой будет действовать одинаковое напряжение - . Действительно, при приложении одноосного напряжения вдоль оси - соответствующее уравнение равновесия среды примет вид - . Откуда следует, что - .Так как деформации каждого типа слоев вдоль оси - есть - , а деформация породы - , то получим следующее выражение

. (5.37)

Используя последовательно (5.16) , (5.37) и (5.22), получим

(или в общем случае для слоев ). (5.38)

Усреднение согласно выражениям (5.38) соответствует определению величины - по закону гармонического средневзвешенного.

Модуль упругости - находится из первого или второго уравнения системы (5.36) при условии равенства нулю соответствующих деформаций. Например, если в первом уравнении положить равными нулю - и , то модуль упругости вдоль слоев - . При этом, деформации в плоскости изотропии будут тем однороднее, чем тоньше будут слои в породе. Складывая силы, приложенные к поперечным сечениям каждого слоя, получим для напряжения - выражение

, (5.39)

где и - напряжения, действующие вдоль соответствующих типов слоев.

Принимая во внимание (5.16), (5.37) , (5.39), условия , и , выпишем систему уравнений для определения модуля упругости

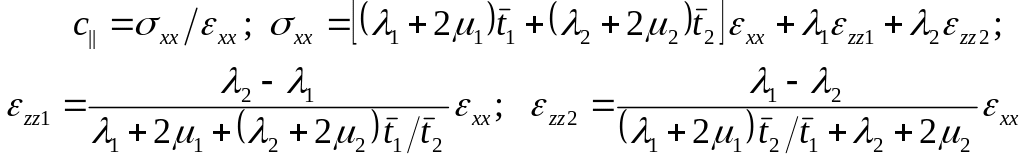. (5.40)

После выполнения алгебраических преобразований с учетом (5.22) окончательно получим

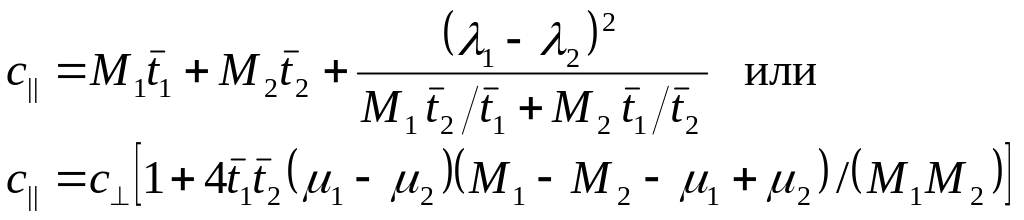. (5.41)

Выражения (5.41) имеют гораздо более сложный вид, нежели выражения (5.38). Это можно понять из следующих рассуждений. При усреднении свойства в трансверсальном направлении (перпендикулярно слоистости) оставшиеся два направления являются эквивалентными, но при усреднении свойства в направлении изотропии (параллельно слоистости) оставшиеся два направления (в направлении изотропии и трансверсальном направлении) уже не являются эквивалентными.

Анализируя выражения (5.41), можно прейти к следующим выводам:

• при 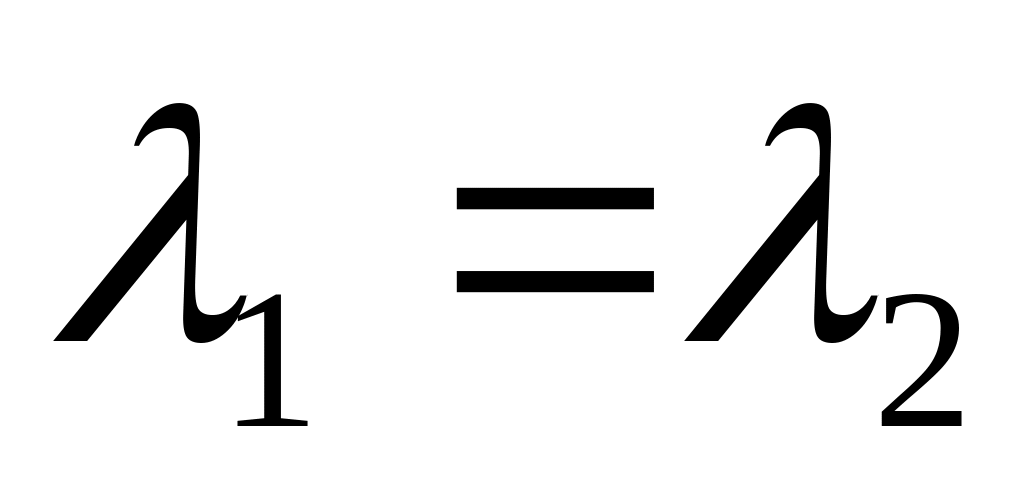выражение для модуля упругости - приобретает вид формулы арифметического средневзвешенного, т.е. - ;

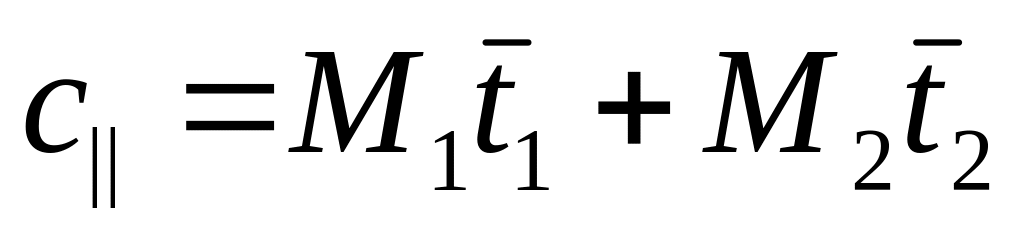• при - 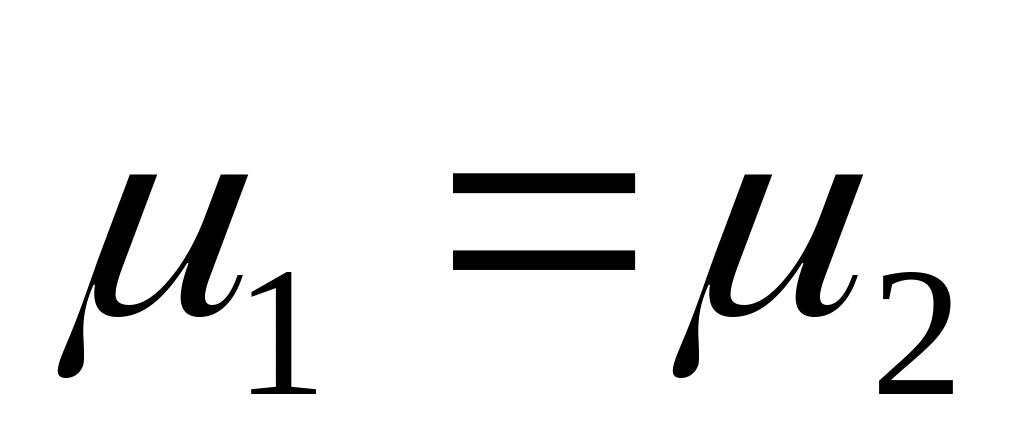коэффициент анизотропии становится равным единице, т.е. слоистая среда ведет себя как изотропная среда при одноосных деформациях вдоль координатных осей.

Процедура усреднения оставшихся параметров трансверсально-изотропной среды ( ) носит похожий характер и может быть распространена на слои произвольных типов. Более подробное рассмотрение вопроса и соответствующая библиография приводятся в [40].

На примере вычисления средних значений модулей упругости - и следует предположить, что при определенных оговорках для ряда физических величин существуют общие правила усреднения в трансверсальной и изотропной плоскостях, которые выражаются формулами гармонического средневзвешенного и арифметического средневзвешенного

; , (5.42)

где - физическая величина, имеющая в зависимости от индекса смысл среднего значения параметра среды или значения параметра слоя.

Легко убедиться, что средние значения модуля Юнга тонкослойной трансверсально-изотропной среды для близких коэффициентов Пуассона слоев удовлетворяют формулам (5.42). В частности, считая горную породу, состоящей из слоев практически одинаковой мощности, и проводя аналогию с параллельными и последовательными соединениями электрических сопротивлений (по виду формул), не сложно установить, что - , т.е. - . Как уже отмечалось выше, этот факт имеет опытное подтверждение.

Для трансверсально-изотропного массива при горизонтальном положении плоскости изотропии формула (5.27), связывающая боковое напряжение с вертикальным напряжением, принимает следующий вид

. (5.43)

В формуле (5.43) обозначения имеют тот же смысл, что и для изотропного массива, но относятся к i-му слою.