5.2.1. Упругие модули изотропных горных пород

Для практического использования уравнений (5.16)-(5.17) необходимо знать упругие постоянные - и . В то же время удобно пользоваться теми величинами, которые могут быть легко получены из измерений для простого напряженно-деформированного состояния, когда значения напряжений и деформаций легко устанавливать и контролировать. Этому условию удовлетворяют модуль всестороннего сжатия, модуль Юнга, коэффициент Пуассона, модуль сдвига, модуль одностороннего сжатия.

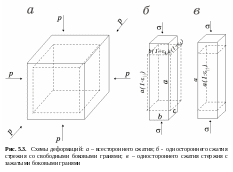Модуль всестороннего сжатия. Всестороннее сжатие реализуется путем создания гидростатического давления (рис. 5.3а). При этом - , , остальные компоненты напряжений и деформаций равны нулю. Используя уравнения (5.16), получим - . Модуль всестороннего сжатия определяется как величина, обратная сжимаемости - . Учитывая, что - , связь между модулем всестороннего сжатия и коэффициентами Ламе имеет вид

. (5.19)

Модуль Юнга. Модуль Юнга определяется при одноосном нагружении сжатия (растяжения) тонкого стержня (рис. 5.3б). Например, если нагружение производится вдоль оси - ( ), то продольная деформация будет - , поперечные деформации - . Используя (5.16), получим систему уравнений - , решение которой и приводит к выражению для модуля Юнга

. (5.20)

Заметим, что выражение для модуля Юнга немедленно следует из первого уравнения системы уравнений (5.17), если положить равными нулю компоненты деформаций за исключением - .

Коэффициент Пуассона. Коэффициент Пуассона определяется как положительная величина, равная отношению поперечной деформации к продольной деформации при одноосном нагружении (рис. 2.2б). Выражение для коэффициента Пуассона следует из второго уравнения системы (5.16)

. (5.21)

Модуль сдвига. Модуль сдвига связывает сдвиговую деформацию с касательным напряжением. Анализируя последние три уравнения системы (5.16), находим - .

Модуль одностороннего сжатия. Модуль одностороннего сжатия определяется в условиях одноосной деформации. Такие условия реализуются, когда образец горной породы помещен в сосуд с жесткими стенками (рис. 5.3в). Заметим, что при одноосной деформации поперечное сечение не изменяется. По этой причине иногда используется другое название модуля как модуля плоской деформации. Похожая ситуация имеет место, когда прикладывается одноосное усилие к горной породе, являющейся жестко закрепленной частью породного массива. Выражение для модуля одностороннего сжатия легко получить из любого из трех первых уравнений системы (5.16), положив соответствующие поперечные деформации равными нулю. Откуда

. (5.22)

Как следует из условий (5.18), модули всестороннего сжатия, Юнга, сдвига и одностороннего сжатия являются положительными величины. Практическая единица размерности этих модулей - МПа. Согласно тем же условиям коэффициент Пуассона может принимать значения в интервале . Однако в природе не найдено тел, которые имели бы отрицательные значения коэффициента Пуассона. Поэтому фактическое значение коэффициента Пуассона лежит в интервале . Это означает, что оба коэффициента Ламе являются положительными величинами, хотя это и не требуется согласно термодинамическим соображениям.

Для кристаллических тел, в которых силы взаимодействия между атомами являются центральными, между рядом упругих постоянных возникают дополнительные соотношения Коши-Пуассона. Для изотропного тела эти соотношения приводят к равенству коэффициентов Ламе, т.е. . Из выражения (5.21) следует, что горные породы, удовлетворяющие соотношениям Коши – Пуассона, имеют коэффициент Пуассона равный - 0,25. К таким породам относятся ряд изверженных интрузивных горных пород с порфировой структурой, равномерным распределением минеральных зерен, например, диорит-порфирит ( ). Отклонения от соотношений Коши-Пуассона наблюдаются для горных пород, обладающих пластичностью – свойством, обусловленным наличием нецентральных сил. Для таких пород, как правило, - .

Если сравнить выражения для модуля всестороннего сжатия (5.19) и модуля одностороннего сжатия (5.22), то легко видеть, что всегда - . Приведенное неравенство имеет простой физический смысл. При всестороннем сжатии происходит только изменение объема тела. При одностороннем сжатии в условиях отсутствия поперечной деформации требуется дополнительное усилие, как на изменение объема, так и на изменение формы тела.

Зная два параметра из пяти - , можно получить остальные параметры. Соответствующие формулы связи для ряда групп из трех параметров представлены в табл. 1.

Таблица 5.1

Формулы связи между часто используемыми упругими модулями

Известные параметры	Искомые параметры
	-	-
		-			-
			-	-
				-	-
	-			-

Анализируя формулы для модулей, выраженных через параметры - , можно установить следующее неравенство: , когда для коэффициента Пуассона выполняется условие - . Большинство скальных и полускальных пород удовлетворяет приведенному условию.

Из физических соображений (не выполняя математических преобразований) можно объяснить неравенство: . Действительно, определение модуля Юнга производится, когда горная порода испытывает изменение объема и изменение формы, т.е. следует ожидать, что - , но при этом боковые стороны нагружаемого образца остаются свободными, поэтому - .

В горной механике закон Гука для изотропного породного массива обычно записывают через модуль Юнга, модуль одностороннего сжатия, модуль сдвига и коэффициент Пуассона. В этом случае системы уравнений (5.16)-(5.17) с использованием тензорных обозначений для напряжений и деформаций примут вид

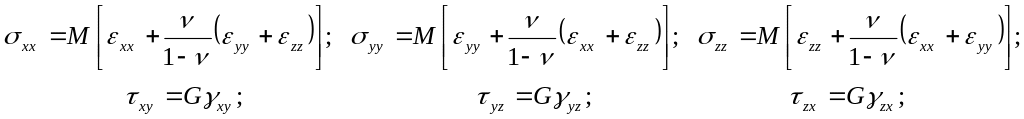(5.23)

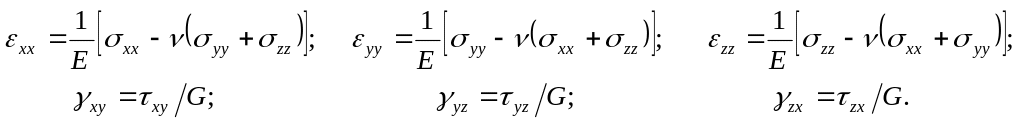(5.24)

В уравнениях (5.23) множитель, стоящий перед круглыми скобками, в геомеханике называется коэффициентом бокового распора, т.е.

. (5.25)

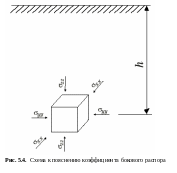
Определим физический смысл коэффициента бокового распора. Выделим в однородном массиве элемент, на который действуют нормальные напряжения (рис. 5.4). На глубине - от дневной поверхности давление, передаваемое со стороны вышележащих слоев пород на нижележащие слои, равно вертикальному сжимающему напряжению - . Такое давление называется литостатическим или горным давлением. Величина напряжения - определяется в виде

, (5.26)

где - объемный вес пород массива.

Так как элемент горной породы зажат с боковых сторон, то поперечные деформации столба равны нулю, т.е. . В силу изотропии массива - . Из уравнений (5.23) и формулы (5.26) следует

. (5.27)

Таким образом, коэффициент бокового распора показывает, какую часть от вертикального напряжения составляет боковое напряжение, которое в свою очередь определяет величину боковой деформации подземной горной выработки или величину давления на крепь выработки. Если принять коэффициент Пуассона равным , то , т.е. . Однако в участках массива, вовлеченных в тектонические процессы, боковые напряжения могут превышать вертикальное напряжение.

Например, в результате складкообразования развиваются мощные сжимающие напряжения, перпендикулярные осям складок - . Вследствие того, что порода в складках находится в состоянии зажима, препятствующего продольному удлинению (вдоль оси складки), возникают сжимающие напряжения в продольном направлении - . В результате получается следующее неравенство - , так как расстояние от элемента породы в складке до дневной поверхности соответствует линии наименьшего сопротивления. Если коэффициент Пуассона стремится к значению , то литостатическое давление переходит в гидростатическое давление, а коэффициент бокового распора – к единице. Однако подобная ситуация реализуется лишь на больших глубинах или, когда вмещающие породы обладают заметной пластичностью.