§4. Соприкасающаяся плоскость к кривой. Главная нормаль. Бинормаль.

Определение. Пусть  – некоторая кривая, P – точка на ней, Q   – близкая к P точка. Пусть  – плоскость, проходящая через P. Обозначим d = PQ,  – расстояние от Q до . Если Combin = 0, то плоскость  называется соприкасающейся плоскостью к кривой  в точке P.

С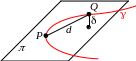 мысл этого определения в следующем: соприкасающаяся плоскость – это та плоскость, которая плотнее всего прилегает к кривой. Следующее определение эквивалентно данному.

Определение. Пусть  – некоторая кривая, P – точка на ней. Выберем две близкие к P точки Q и R на кривой. Если при Q ^– P и R ^– P плоскость PQR стремится занять определенное положение , то плоскость  называется соприкасающейся плоскостью к кривой  в точке P.

Теорема 2. Если кривая  дважды дифференцируема в точке P, то она имеет в этой точке соприкасающуюся плоскость. Если c(t) – параметризация класса C² кривой  и P = c(t_o), то соприкасающаяся плоскость будет параллельна векторам c(t_o) и c(t_o). Если эти векторы неколлинеарны, то соприкасающаяся плоскость единственна, а если c(t_o) c(t_o), то любая плоскость, проходящая через касательную к кривой  в точке P, будет соприкасающейся плоскостью к кривой.

Можно определить соприкасающуюся плоскость, как паралелльную векторам c(t_o) и c(t_o), а потом доказать, что именно она наиболее плотно прилегает к кривой.

Если c(t_o) ((;\s\do3( ∕ c(t_o), то соприкасающаяся плоскость в точке P = c(t_o) задается уравнением

x – x_o y – y_o z – z_o

c₁ c₂ c₃ = 0 .

c₁ c₂ c₃

Определение. Прямая перпендикулярная к соприкасающейся плоскости к кривой  в точке P называется бинормалью к кривой  в точке P. Нормаль к кривой  в точке P, лежащая в соприкасающейся плоскости называется главной нормалью.

Поскольку c(t_o) и c(t_o) параллельны соприкасающейся плоскости, то вектор c(t_o)c(t_o) будет вектором нормали к ней, а значит, он будет направляющим вектором бинормали. Значит, бинормаль задается уравнением

= = .

c₂ c₃ c₃ c₁ c₂ c₃

Г лавная нормаль перпендикулярна касательной и бинормали. Поэтому ее направляющий вектор перпендикулярен c и cc. Значит, направляющий вектор главной нормали – это (c c) c. Для того, чтобы составить уравнение главной нормали надо сначала вычислить этот вектор в данной точке.

Определение. Плоскость перпендикулярная главной нормали к кривой  в точке P называется спрямляющей плоскостью к кривой  в точке P.

Для спрямляющей плоскости вектор (cc)c будет вектором нормали. Для того, чтобы составить уравнение спрямляющей плоскости надо сначала вычислить вектор (cc)c в данной точке.

Единичные направляющие векторы касательной, главной нормали и бинормали принято обозначать соответственно , , . Тогда, для того, чтобы они образовывали правую тройку необходимо, чтобы выполнялось  =    – именно в этом порядке. Тогда

 = ,  = ,  = .

Говорят, что вместе с точкой P = c(t_o) эти векторы, вычисленные в данной точке, образуют подвижной репер кривой {P, , , } или репер Френе. Именно в этом репере удобнее всего исследовать поведение кривой в окрестности точки P.

И зобразим теперь вместе все прямые и плоскости, относящиеся к кривой.