Глава 1. Элементы топологии. §1. Понятие метрического пространства. Расстояние между множествами. Диаметр множества.

Напомним, что в точечном евклидовом пространстве Eⁿ расстояние между точками P(x₁, x₂,… x_n), Q(y₁, y₂,… y_n) вычисляется по формуле

(P, Q) = ,

если координаты точек заданы относительно ортонормированной системы координат. Мы можем рассматривать это расстояние, как функцию, сопоставляющую двум точкам P и Q число (P, Q). Функция  обладает следующими свойствами:

1. (P, Q) = (Q, P);

2. (P, Q) + (Q, R)  (P, R) (неравенство треугольника);

3. (P, Q)  0, и (P, Q) = 0  P = Q.

Пусть теперь M – произвольное множество, элементы которого будем называть точками. Пусть на M задана функция , сопоставляющая любым двум точкам P, QM число (P, Q), которое называется расстоянием между этими точками, и такая что выполнены свойства (аксиомы) 1, 2, 3. Тогда пара (M, ) называется метрическим пространством, а функция  – метрикой.

Примеры 1. Пусть V – произвольное подмножество евклидова пространства. Расстояние между двумя точками P, QV будем считать таким же, как во всем пространстве. Тогда (V, ) – метрическое пространство. Метрика  называется индуцированной из Eⁿ.

2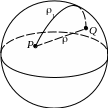 . Сфера S² в трехмерном геометрическом пространстве. Расстояние ₁ между P, Q S² определяется как длина кратчайшей кривой по поверхности, соединяющей P и Q. Как известно, этой кривой является дуга большой окружности (у которой радиус равен радиусу сферы).

Мы также можем определить расстояние как в примере 1: (P, Q) – это длина хорды PQ. Тогда (S², ₁) и (S², ) – это разные метрические пространства.

3. Определим на плоскости расстояние между точками A(x₁, y₁), B(x₂, y₂) по формуле ₂(A, B)=|x₂  x₁|+|y₂  y₁|. Получается, что ₂(A, B) равно длине ломаной AMB, изображённой на следующем чертеже.

У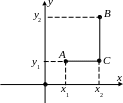 пражнение. Самостоятельно про-верьте, что для плоскости с метрикой ₂ выполняются все аксиомы метрического пространства.

Диаметром множества V в метрическом пространстве (M, ) называется точная верхняя грань расстояний между точками этого множества:

d(V) = sup;\s\do10(P (P, Q).

Расстоянием между двумя множествами V, W называется точная нижняя грань расстояний между точками этих множеств:

(V, W) = inf;\s\do10(P(V (P, Q).

В частности, если одно из множеств состоит из одной точки, то получаем определение расстояния от точки до множества.

П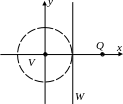 очему в этом определении супрэмум, а не максимум, инфинум, а не минимум? Поясним на примере.

Пример. Пусть V – это открытый (без границы) круг радиуса 1 на плоскости с центром в начале координат, а W = Q(2,0). Тогда d(V) = 2, хотя таких точек, расстояние между которыми равно 2 в V нет. Таким образом, максимум не достигается. Аналогично, (Q, V) = 1, хотя такой точки PV, что (Q, P) = 1 не существует. Значит, минимум не достигается.

Отметим, что если множества пересекаются, то расстояние между ними равно нулю. Обратное неверно. Например, если W есть прямая x = 1, то (V, W) = 0, но V W=.

Определение. Множество V в метрическом пространстве (M, ) называется ограниченным, если d(V)<.

Заметим, что и всё метрическое пространство может быть ограниченным, как например, (S², ₁).

Упражнение. Чему равны диаметры метрических пространств (S², ₁) и (S², )?