Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу

Тогда -двойной интеграл Фурье.

Окончательно получаем:

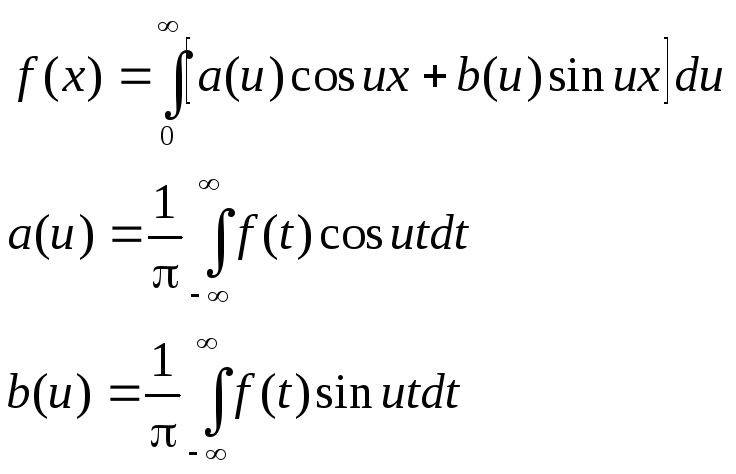
- представление функции f(x)интегралом Фурье.

Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:

Преобразование Фурье.

Определение.Еслиf(x)– любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция

называется преобразованием Фурье функции f(x).

Функция F(u)называется такжеспектральной характеристикой функции f(x).

Если f(x) – функция, представимая интегралом Фурье, то можно записать:

Это равенство называется обратным преобразованием Фурье

Интегралы иназываются соответственнокосинус - преобразование Фурье и синус – преобразование Фурье.

Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных.

Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.

Элементы теории функций комплексного переменного.

Определение.Если каждому комплексному числуzиз некоторого множестваDпо некоторому закону поставлено в соответствие определенное комплексное числоwиз множестваG, то на этой области заданаоднозначная функция комплексного переменного, отображающая множествоDна множествоG.

w = f(z)

Множество Dназываетсяобластью определения, множествоG–областью значений функции.

Комплексную функцию можно записать в виде:

u, v– действительные функции от переменныххиу.

Если каждому zDсоответствует несколько различных значенийw, то функцияw=f(z)называетсямногозначной.

Определение.Функция имеетпределв точкеz₀, равный числуА = a + ib, если

Свойства функций комплексного переменного.

Для функций комплексного переменного f(z)иg(z)справедливы следующие свойства:

1)

2)

3)

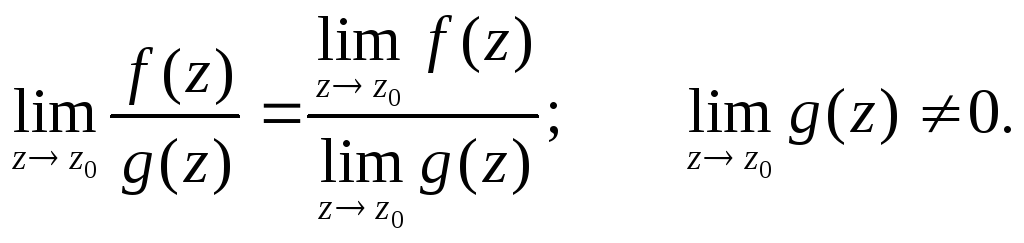
Определение.Функция называетсянепрерывнойв точкеz₀, если выполняется равенство

Основные трансцендентные функции.

Определение. Трансцендентныминазываются аналитические функции, которые не являются алгебраическими.

Если аргументом показательной или тригонометрических функций является комплексное число, то определение этих функций, вводимое в элементарной алгебре теряет смысл.

Рассмотрим разложение в степенной ряд следующих функций:

См.Представление функций по формуле Тейлора.

Функции e^z,cosz,sinzсвязаны между собой формулой Эйлера (см.Уравнение Эйлера.) Эта формула может быть очень легко получена сложением соотвествующих рядов.

Также справедливы равенства:

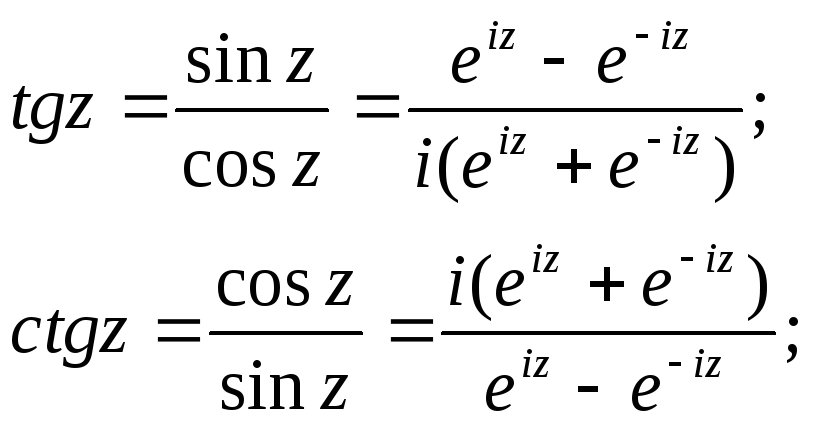
Для тригонометрических функций комплексного аргумента справедливы основные тригонометрические тождества (синус и косинус суммы, разности и т.д.), которые справедливы для функций действительного аргумента.

Определение.Гиперболическим синусом, косинусом, тангенсом и котангенсом называются соответственно функции:

Гиперболические функции могут быть выражены через тригонометрические:

Гиперболические функцииsh z иch zимеют период 2i, а функцииth zиcth z– периодi.

Пример. Найти sin(1+2i).

Определение. Логарифмическая функциякомплексного аргумента определяется как функция, обратная показательной.

Еслиw = u + iv,тоиArg e^w = = v.

Тогда e^u = .

Итого:

Для комплексного числа z = a + ib

Определение.Выражение называетсяглавным значением логарифма.

Логарифмическая функция комплексного аргумента обладает следующими свойствами:

1)

2)

3)

4)

Обратные тригонометрические функциикомплексного переменного имеют вид:

Производная функций комплексного переменного.

Определение.Производнойот однозначной функцииw = f(z)в точкеzназывается предел:

Определение.Функцияf(z), имеющая непрерывную производную в любой точке областиDназываетсяаналитическойфункцией на этой области.

Правила дифференцирования функций комплексного аргумента не отличаются от правил дифференцирования функций действительной переменной.

Аналогично определяются производные основных функций таких как синус, косинус, тангенс и котангенс, степенная функция и т.д.

Производные гиперболических функций определяются по формулам:

Вывод правил интегрирования, значений производных основных функций ничем не отличается от аналогичных операций с функциями действительного аргумента, поэтому подробно рассматривать их не будем.

Условия Коши – Римана.

(Бернхард Риман (1826 – 1866) – немецкий математик)

Рассмотрим функцию комплексной переменной , определенную на некоторой области и имеющую в какой – либо точке этой области производную

Стремление к нулюz0 может осуществляться в следующих случаях:

1)

2)

В первом случае:

Во втором случае:

Тогда должны выполняться равенства:

Эти равенства называются условиями Коши – Римана, хотя еще раньше они были получены Эйлером и Даламбером.

Теорема.Если функция имеет производную в точке

z = x + iy, то ее действительные компоненты u и v имеют в точке (х, у) частные производные первого порядка, удовлетворяющие условию Коши – Римана.

Также справедлива и обратная теорема.

На основании этих теорем можно сделать вывод, что из существования производной следует непрерывность функции.

Теорема.Для того, чтобы функция была аналитической на некоторой области необходимо и достаточно, чтобы частные производные первого прядка функцийu и v были непрерывны на этой области и выполнялись условия Коши – Римана.

Интегрирование функций комплексной переменной.

Пусть - непрерывная функция комплексного переменногоz, определенная в некоторой области иL– кривая, лежащая в этой области.

у

В

L

А

х

Кривая Lзадана уравнением

Определение.Интеграл от функцииf(z) вдоль кривойLопределяется следующим образом:

Если учесть, что , то

Теорема.(Теорема Коши)Если f(z) - аналитическая функция на некоторой области, то интеграл от f(z) по любому кусочно – гладкому контуру, принадлежащему этой области равен нулю.

Интегральная формула Коши.

Если функция f(z)– аналитическая в односвязной замкнутой области с кусочно – гладкой границейL.

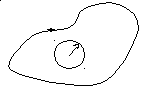
D



z₀

Тогда справедлива формула Коши:

где z₀– любая точка внутри контураL, интегрирование по контуру производится в положительном направлении (против часовой стрелки).

Эта формула также называется интегралом Коши.

Ряды Тейлора и Лорана.

(Пьер Альфонс Лоран (1813 – 1854) – французский математик)

Функция f(z), аналитическая в круге, разлагается в сходящийся к ней степенной ряд по степеням (z–z₀).

Коэффициенты ряда вычисляются по формулам:

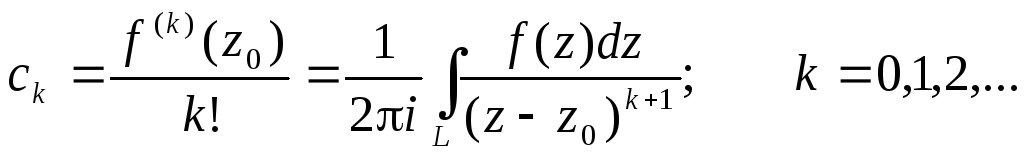
Степенной ряд с коэффициентами такого вида называетсярядом Тейлора.

Рассмотрим теперь функцию f(z), аналитическую в кольце . Эта функция может быть представлена в виде сходящегося ряда:

Ряд такого вида называетсярядом Лорана. При этом функцияf(z) может быть представлена в виде суммы:

Ряд, определяющий функциюf₁(x), называетсяправильной частьюряда Лорана, а ряд, определяющий функциюf₂(x),называетсяглавной частью ряда Лорана.

Если предположить, что r = 0, то можно считать, что функция аналитична в открытом круге за исключением центральной точкиz₀. Как правило, в этой точке функция бывает не определена.

Тогда точкаz₀называетсяизолированной особой точкой функцииf.

Рассмотрим следующие частные случаи:

1) Функция f(x) имеет вид: . Т.к. степенной ряд сходится во всех точках внутри круга, то его суммаf₁(x) определена и непрерывно дифференцируема во всех точках круга, а, следовательно, и в центре кругаz₀.

В этом случае говорят, что особенность функции f в точке z₀ устранима.Для устранения особой точки достаточно доопределить функцию в центре круга (f(z₀) =c₀) и функция будет аналитической не только в окрестности центра круга, но и в самом центре.

В этом случае для любого контураL, содержащего точкуz₀и принадлежащего к кругу.

2) Функция f(x) имеет вид: .

В этом случае точка z₀называетсяполюсом функции f(z) порядка (кратности) m. Приm= 1 точкуz₀называют ещепростым полюсом.

Порядок полюса может быть определен по формуле:

z₀– полюс порядкат.

3) Функция f(z) имеет вид , где в ряду не равно нулю бесконечное количество коэффициентовс_-k.

В этом случае говорят, что функция f(z) имеет в точкеz₀существенно особую точку.

Определение.Пустьz₀– изолированная особая точка функцияf(z), т.е. пусть функцияf(z) – аналитическая в некотором кругеиз которого исключена точкаz₀. Тогда интеграл

называется вычетомфункцииf(z) в точкеz₀, гдеL– контур в круге, ориентированный против часовой стрелки и содержащей в себе точкуz₀.

Вычет также обозначают иногда .

Если есть ряд Лорана функцииfв точкеz₀, то.

Таким образом, если известно разложение функции в ряд Лорана, то вычет легко может быть найден в случае любой особой точки.

В частных случаях вычет может быть найден и без разложения в ряд Лорана.

Например, если функция , аимеет простой нуль приz=z₀ , тоz=z₀является простым полюсом функцииf(z).

Тогда можно показать, что вычет находится по формуле

Еслиz=z₀– полюс порядкаm1, то вычет может быть найден по формуле:

Пример.Найти вычет функцииотносительно точкиz= 2.

Эта точка является полюсом второго порядка. Получаем:

Теорема о вычетах.

Теорема.Пусть функция f(z) – аналитическая на всей плоскости z, за исключением конечного числа точек z₁, z₂, …, z_N. Тогда верно равенство:

А интеграл от функции по контуру L, содержащему внутри себя эти точки, равен

Эти свойства применяются для вычисления интегралов. Если функцияf(z) аналитическая в верхней полуплоскости, включая действительную ось, за исключениемNточек, то справедлива формула

Пример.Вычислить определенный интеграл .

Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки 2i. Эта точка является полюсом второго порядка.

Найдем вычет функции

Получаем

Пример.Вычислить определенный интеграл

Подынтегральная функция является аналитической в верхней полуплоскости за исключением точки i. Эта точка является полюсом второго порядка.

Найдем вычет функции

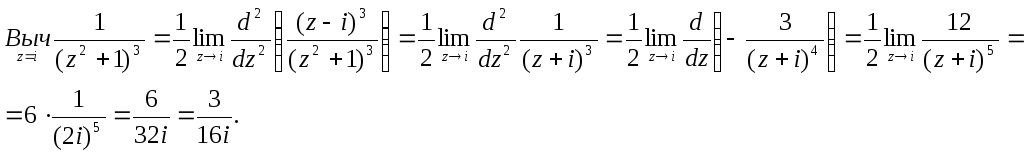
Получаем

Назад, в начало комплекса.

Содержание. Часть1.

Введение в математический анализ.

Числовая последовательность.

Ограниченные и неограниченные последовательности.

Предел.

Монотонные последовательности.

Число е.

Связь натурального и десятичного логарифмов.

Предел функции в точке.

Односторонние пределы.

Предел функции при стремлении аргумента к бесконечности.

Основные теоремы о пределах.

Ограниченные функции.

Бесконечно малые функции.

Свойства бесконечно малых функций.

Бесконечно большие функции и их связь с бесконечно малыми.

Сравнение бесконечно малых функций.

Свойства эквивалентных бесконечно малых функций.

Некоторые замечательные пределы.

Непрерывность функции в точке.

Разрывная функция.

Непрерывная функция.

Свойства непрерывных функций.

Непрерывность некоторых элементарных функций.

Точки разрыва и их классификация.

Непрерывность функции на интервале и на отрезке.

Свойства функций, непрерывных на отрезке.

Равномерно непрерывные функции.

Комплексные числа.

Тригонометрическая форма числа.

Действия с комплексными числами.

Формула Муавра.

Показательная форма комплексного числа.

Уравнение Эйлера.

Дифференциальное исчисление функций одной переменной.

Производная функции, ее геометрический и физический смысл.

Уравнение касательной и нормали к кривой.

Односторонние производные функции в точке.

Основные правила дифференцирования.

Производные основных функций.

Производная сложной функции.

Логарифмическое дифференцирование.

Производная показательно – степенной функции.

Производная обратной функции.

Дифференциал функции.

Геометрический смысл дифференциала.

Свойства дифференциала.

Дифференциал сложной функции. Инвариантная форма записи.

Формула Тейлора.

Формула Лагранжа.

Формула Маклорена.

Представление функций по формуле Тейлора.

Бином Ньютона.

Применение дифференциала к приближенным вычислениям.

Теоремы о среднем.

Теорема Ролля.

Теорема Лагранжа.

Теорема Коши.

Раскрытие неопределенностей. Правило Лопиталя.

Производная и дифференциалы высших порядков.

Правила нахождения производных.

Исследование функций.

Возрастание и убывание функций.

Точки экстремума.

Критические точки.

Достаточные условия экстремума.

Исследование функций с помощью производных высших порядков.

Выпуклость и вогнутость кривой.

Точки перегиба.

Асимптоты.

Схема исследования функций.

Векторная функция скалярного аргумента.

Уравнение касательной к кривой.

Свойства производной векторной функции скалярного аргумента.

Уравнение нормальной плоскости.

Параметрическое задание функции.

Окружность.

Эллипс.

Циклоида.

Астроида.

Производная функции, заданной параметрически.

Кривизна плоской кривой.

Угол смежности.

Средняя кривизна.

Кривизна дуги в точке.

Радиус кривизны.

Центр и круг кривизны.

Эволюта и эвольвента.

Свойства эволюты.

Кривизна пространственной кривой.

Годограф.

Главная нормаль.

Вектор и радиус кривизны.

Формулы Френе.

Соприкасающаяся плоскость.

Бинормаль.

Кручение кривой.

Назад, в начало комплекса.

Содержание. Часть вторая.

Интегральное исчисление.

Первообразная функция.

Неопределенный интеграл.

Свойства неопределенного интеграла.

Таблица основных интегралов.

Непосредственное интегрирование.

Способ подстановки.

Интегрирование по частям.

Интегрирование элементарных дробей.

Рекуррентная формула.

Интегрирование рациональных функций.

Интегрирование рациональных дробей.

Метод неопределенных коэффициентов.

Метод произвольных значений.

Интегрирование тригонометрических функций.

Универсальная тригонометрическая подстановка.

Интегрирование иррациональных функций.

Биноминальные дифференциалы.

Тригонометрическая подстановка.

Подстановки Эйлера.

Метод неопределенных коэффициентов.

Интегралы, не выражающиеся через элементарные функции.

Эллиптические интегралы.

Интеграл Пуассона.

Интеграл Френеля.

Интегральный логарифм.

Интегральный синус и косинус.

Определенный интеграл.

Интегральная сумма.

Интегрируемая функция.

Свойства определенного интеграла.

Теорема о среднем.

Обобщенная теорема о среднем.

Вычисление определенного интеграла.

Теорема Ньютона – Лейбница.

Замена переменных в определенном интеграле.

Интегрирование по частям.

Приближенное вычисление определенного интеграла.

Формула прямоугольников.

Формула трапеций.

Формула парабол (Симпсона).

Несобственные интегралы.

Абсолютная сходимость интеграла.

Интеграл от разрывной функции.

Нахождение площадей плоских фигур.

Нахождение площади криволинейного сектора.

Вычисление длины дуги кривой.

Вычисление объемов тел по поперечным сечениям.

Вычисление объемов тел вращения.

Площадь поверхности тела вращения.

Функции нескольких переменных.

Предел.

Непрерывность.

Наибольшее и наименьшее значения.

Частное приращение.

Частная производная.

Геометрический смысл частных производных.

Полное приращение и полный дифференциал.

Касательная плоскость и нормаль к поверхности.

Приближенные вычисления с помощью полного дифференциала.

Частные производные и дифференциалы высших порядков.

Экстремум функции нескольких переменных.

Необходимые условия экстремума.

Достаточные условия экстремума.

Условный экстремум.

Функция Лагранжа.

Производная по направлению.

Направляющие косинусы.

Градиент.

Связь градиента с производной по направлению.

Кратные интегралы.

Двойные интегралы.

Условия существования двойного интеграла.

Свойства двойного интеграла.

Вычисление двойного интеграла.

Замена переменных в двойном интеграле.

Якобиан.

Двойной интеграл в полярных координатах.

Тройной интеграл.

Замена переменных в тройном интеграле.

Цилиндрическая система координат.

Сферическая система координат.

Геометрические и физические приложения кратных интегралов.

Ряды.

Основные определения.

Свойства рядов.

Критерий Коши.

Ряды с неотрицательными членами.

Признак сравнения.

Признак Даламбера.

Предельный признак Даламбера.

Признак Коши.

Интегральный признак Коши.

Знакопеременные ряды.

Знакочередующиеся ряды.

Признак Лейбница.

Абсолютная и условная сходимость рядов.

Признак Даламбера и Коши для знакопеременных рядов.

Свойства абсолютно сходящихся рядов.

Функциональные последовательности.

Область сходимости.

Функциональные ряды.

Критерий Коши равномерной сходимости.

Признак Вейерштрасса.

Свойства равномерно сходящихся рядов.

Степенные ряды.

Теоремы Абеля.

Радиус сходимости.

Действия со степенными рядами.

Разложение функций в степенные ряды.

Решение дифференциальных уравнений с помощью степенных рядов.

Ряды Фурье.

Тригонометрический ряд.

Коэффициенты Фурье.

Достаточные признаки разложимости в ряд Фурье.

Разложение в ряд Фурье непериодической функции.

Ряд Фурье для четных и нечетных функций.

Ряд Фурье для функций любого периода.

Ряд Фурье по ортогональной системе функций.

Интеграл Фурье.

Преобразование Фурье.

Элементы теории функций комплексной переменной.

Свойства функций комплексной переменной.

Основные трансцендентные функции.

Производная функций комплексной переменной.

Условия Коши – Римана.

Интегрирование функций комплексного переменного.

Теорема Коши.

Интегральная формула Коши.

Ряды Тейлора и Лорана.

Изолированные особые точки.

Теорема о вычетах.

Вычисление интегралов с помощью вычетов.

Назад, в начало комплекса.

Назад, в начало комплекса.