Тема 9. Функция нескольких переменных. Её предел, дифференцируемость, непрерывность. Экстремум и условный экстремум.

Понятие функции нескольких переменных. Непрерывность функции нескольких переменных. Повторные пределы. Бесконечные пределы. Дифференцируемость функции нескольких переменных. Необходимое и достаточное условия дифференцируемости функции в точке. Дифференцируемость сложной функции. Частные производные. Правила дифференцирования. Дифференциал, его геометрический смысл. Инвариантность формы первого дифференциала. Формула конечных приращений Лагранжа. Дифференциалы высших порядков. Касательная плоскость к графику функции двух переменных. Производная по направлению. Градиент. Формула Тейлора для функции нескольких переменных. Необходимые и достаточные условия экстремума. Условный экстремум. Метод множителей Лагранжа.

Назад, в начало комплекса.

4. Список рекомендуемой литературы.

(использовать можно любое доступное издание приведённых ниже учебных пособий).

1. Бугров Я.С., Никольский С.М.: Дифференциальное и интегральное исчисление. М. Высшая школа, 1993.

2. Бугров Я.С., Никольский С.М.: Высшая математика (задачник). М. Высшая школа, 1993.

3. Выгодский М.Я.: Справочник по высшей математике. М. Просвещение, 2002.

4. Демидович Б.П.: Задачи и упражнения по математическому анализу для ВТУЗов. Высшая школа, 1986.

5. Ильин В.А, Поздняк Э.Г.: Основы математического анализа. М. Высшая школа, 1994.

6. Кудрявцев Л.Д.: Курс математического анализа. М. Высшая школа, 1998.

7. Кудрявцев Л.Д.: и др. Сборник задач по математическому анализу (ч.1 и 2). М. Высшая школа, 1998.

8. Кузнецов Л.А.: Сборник задач по высшей математике (типовые расчёты). М. Просвещение, 1983.

9. Мантуров О.В.: Матвеев Н.М. Курс высшей математики. М. Высшая школа, 1996.

10. Минорский В.П.: Сборник задач по высшей математике (ч.1 и 2). Наука, 1982.

11. Миносцев В.Б.: Курс высшей математики. М. РИЦ МГИУ, 2001.

12. Щипачёв В.С.: Высшая математика (для экономических специальностей). М. Высшая школа, 2001.

Назад, в начало комплекса.

Назад, в начало комплекса.

Часть вторая. Конспект лекций по дисциплине “Математический анализ”.

Содержание. Часть 1.

Содержание. Часть 2.

МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Часть 1 Введение в математический анализ.

Числовая последовательность.

Определение.Если каждому натуральному числуnпоставлено в соответствие число х_n, то говорят, что заданапоследовательность

x_1, х₂, …, х_n = {x_n}

Общий элемент последовательности является функцией отn.

x_n=f(n)

Таким образом последовательность может рассматриваться как функция.

Задать последовательность можно различными способами – главное, чтобы был указан способ получения любого члена последовательности.

Пример.{x_n} = {(-1)ⁿ} или {x_n} = -1; 1; -1; 1; …

{x_n} = {sinn/2} или {x_n} = 1; 0; 1; 0; …

Для последовательностей можно определить следующие операции:

1. Умножение последовательности на число m:m{x_n} = {mx_n}, т.е.mx₁,mx₂, …

2. Сложение (вычитание) последовательностей: {x_n}{y_n} = {x_ny_n}.

3. Произведение последовательностей: {x_n}{y_n} = {x_ny_n}.

4. Частное последовательностей: 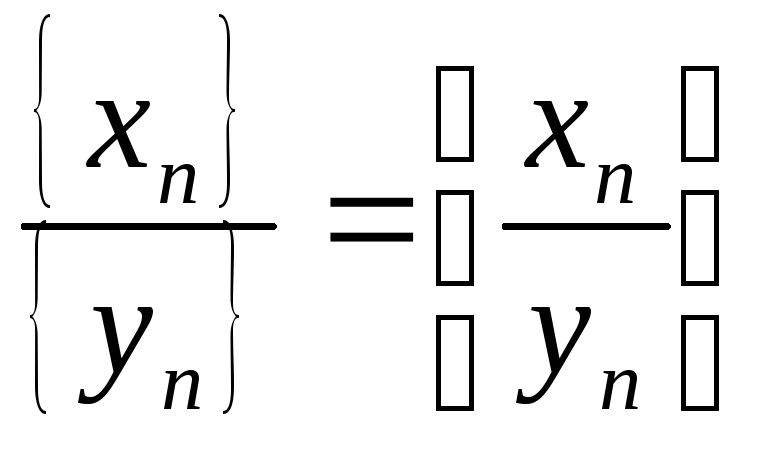при{y_n}  0.

Ограниченные и неограниченные последовательности.

Определение.Последовательность {x_n} называетсяограниченной, если существует такое число М>0, что для любогоnверно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение.Последовательность {x_n}называетсяограниченной сверху, если для любогоnсуществует такое число М, что

x_n M.

Определение.Последовательность {x_n}называетсяограниченной снизу, если для любогоnсуществует такое число М, что

x_n M

Пример.{x_n} =n– ограничена снизу {1, 2, 3, … }.

Определение.Числоаназываетсяпределомпоследовательности {x_n}, если для любого положительного>0 существует такой номерN, что для всехn>Nвыполняется условие:

Это записывается: limx_n=a.

В этом случае говорят, что последовательность {x_n}сходитсяк а приn.

Свойство:Если отбросить какое- либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример.Доказать, что предел последовательностиlim .

Пусть при n>Nверно , т.е.. Это верно при, таким образом, если заNвзять целую часть от, то утверждение, приведенное выше, выполняется.

Пример.Показать, что приnпоследовательность 3, имеет пределом число 2.

Итого: {x_n}= 2 + 1/n; 1/n=x_n– 2

Очевидно, что существует такое число n, что, т.е.lim{x_n} = 2.

Теорема.Последовательность не может иметь более одного предела.

Доказательство.Предположим, что последовательность {x_n}имеет два пределаaиb, не равные друг другу.

x_na;x_nb;ab.

Тогда по определению существует такое число >0, что

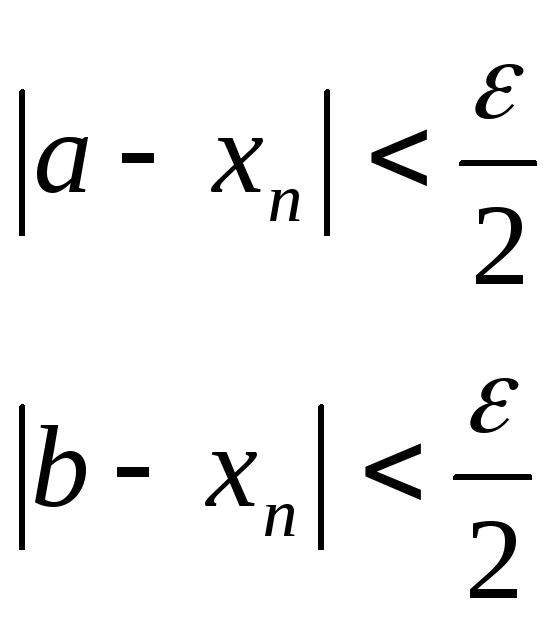
Запишем выражение:

А т.к. -любое число, то, т.е.a=b. Теорема доказана.

Теорема.Если x_n  a, то.

Доказательство.Изx_n  aследует, что. В то же время:

, т.е., т.е.. Теорема доказана.

Теорема.Если x_n  a, то последовательность {x_n} ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность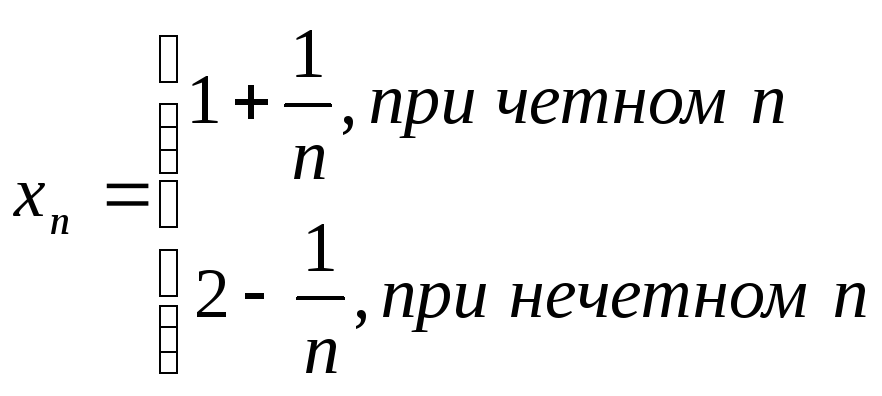не имеет предела, хотя

Монотонные последовательности.

Определение.1) Еслиx_n+1>x_nдля всехn, то последовательность возрастающая.

2)Если x_n+1x_nдля всехn, то последовательность неубывающая.

3)Если x_n+1<x_nдля всехn, то последовательность убывающая.

4)Если x_n+1x_nдля всехn, то последовательность невозрастающая

Все эти последовательности называются монотонными.Возрастающие и убывающие последовательности называютсястрого монотонными.

Пример.{x_n} = 1/n– убывающая и ограниченная

{x_n} =n– возрастающая и неограниченная.

Пример.Доказать, что последовательность {x_n}=монотонная возрастающая.

Найдем член последовательности {x_n+1}=

Найдем знак разности: {x_n}-{x_n+1}=

, т.к.nN, то знаменатель положительный при любомn.

Таким образом, x_n+1>x_n. Последовательность возрастающая, что и следовало доказать.

Пример.Выяснить является возрастающей или убывающей последовательность

{x_n} = .

Найдем . Найдем разность

, т.к.nN, то 1 – 4n<0, т.е. х_n+1<x_n. Последовательность монотонно убывает.

Следует отметить, что монотонные последовательности ограничены по крайней мере с одной стороны.

Теорема.Монотонная ограниченная последовательность имеет предел.

Доказательство.Рассмотрим монотонную неубывающую последовательность

х₁х₂х₃…х_nx_n+1…

Эта последовательность ограничена сверху: x_nM, где М – некоторое число.

Т.к. любое, ограниченное сверху, числовое множество имеет четкую верхнюю грань, то для любого >0 существует такое числоN, чтоx_N>a-, где а – некоторая верхняя грань множества.

Т.к. {x_n}- неубывающая последовательность, то приN>nа -<x_Nx_n,

x_n > a - .

Отсюда a -  < x_n < a + 

- < x_n – a <  или x_n - a< , т.е. lim x_n = a.

Для остальных монотонных последовательностей доказательство аналогично.

Теорема доказана.

Число е.

Рассмотрим последовательность {x_n} = .

Если последовательность {x_n} монотонная и ограниченная, то она имеет конечный предел.

По формуле бинома Ньютона:

или, что то же самое

Покажем, что последовательность {x_n} – возрастающая. Действительно, запишем выражениеx_n+1и сравним его с выражениемx_n:

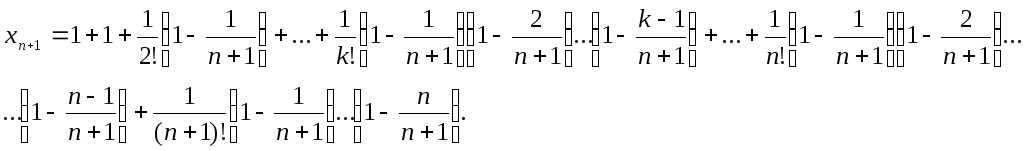Каждое слагаемое в выраженииx_n+1больше соответствующего значенияx_n, и, кроме того, уx_n+1добавляется еще одно положительное слагаемое. Таким образом, последовательность {x_n} возрастающая.

Докажем теперь, что при любом nее члены не превосходят трех:x_n< 3.

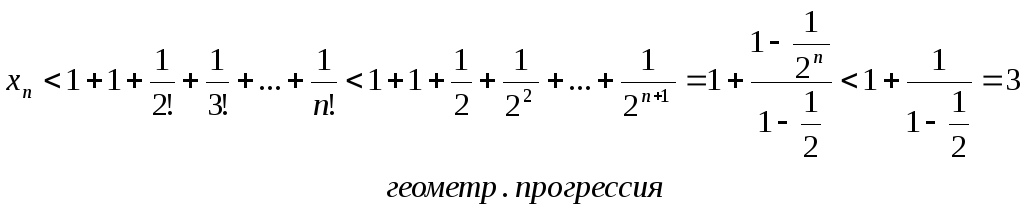
Итак, последовательность - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.

Из неравенства следует, что е3. Отбрасывая в равенстве для {x_n} все члены, начиная с четвертого, имеем:

переходя к пределу, получаем

Таким образом, число е заключено между числами 2,5 и 3. Если взять большее количество членов ряда, то можно получить более точную оценку значения числа е.

Можно показать, что число е иррациональное и его значение равно 2,71828…

Аналогично можно показать, что , расширив требования к х до любого действительного числа:

Предположим:

Найдем

Число е является основанием натурального логарифма.

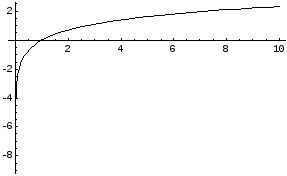
Выше представлен график функции y=lnx.

Связь натурального и десятичного логарифмов.

Пусть х = 10^у, тогдаlnx=ln10^y, следовательноlnx=yln10

у = , где М = 1/ln100,43429…- модуль перехода.

Предел функции в точке.

yf(x)

A+

A

A-

0 a-aa+x

Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)

Определение.Число А называетсяпределомфункцииf(x) при ха, если для любого>0 существует такое число>0, что для всех х таких, что

0 < x-a<

верно неравенство f(x) -A<.

То же определение может быть записано в другом виде:

Если а - <x<a+,xa, то верно неравенство А -<f(x) <A+.

Запись предела функции в точке:

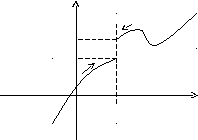
Определение.Еслиf(x)A₁при ха только приx<a, то- называетсяпределомфункцииf(x) в точке х = аслева, а еслиf(x)A₂при ха только приx>a, тоназываетсяпределомфункцииf(x) в точке х = асправа.

у

f(x)

А₂

А₁

0 ax

Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.

Пределы А₁и А₂называются такжеодносторонними пределамифункцииf(x) в точке х = а. Также говорят, что А –конечный пределфункцииf(x).

Предел функции при стремлении аргумента к бесконечности.

Определение.Число А называетсяпределомфункцииf(x) при х, если для любого числа>0 существует такое число М>0, что для всех х,х>Mвыполняется неравенство

При этом предполагается, что функция f(x) определена в окрестности бесконечности.

Записывают:

Графически можно представить:

yy

AA

0 0

xx

yy

AA

0 0

xx

Аналогично можно определить пределы для любого х>Mи

для любого х<M.

Основные теоремы о пределах.

Теорема 1., где С =const.

Следующие теоремы справедливы при предположении, что функции f(x) иg(x) имеют конечные пределы при ха.

Теорема 2.

Доказательство этой теоремы будет приведено ниже.

Теорема 3.

Следствие.

Теорема 4. 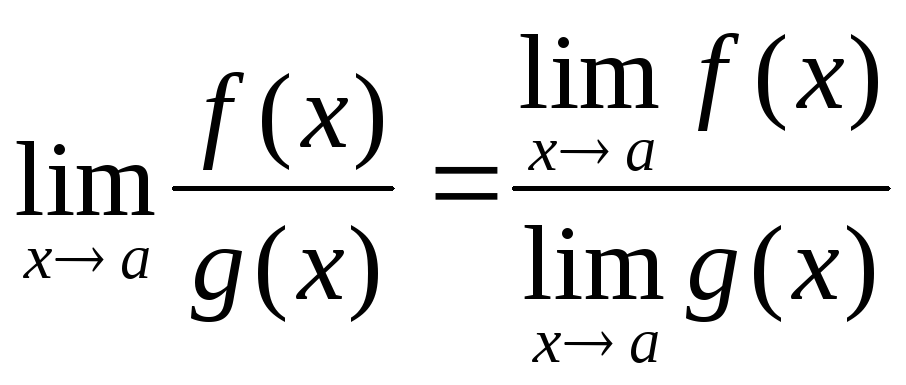при

Теорема 5.Если f(x)>0 вблизи точки х = а и , то А>0.

Аналогично определяется знак предела при f(x) < 0,f(x)0,f(x)0.

Теорема 6.Если g(x)  f(x)  u(x) вблизи точки х = а и , то и.

Определение.Функцияf(x) называетсяограниченной вблизи точки х = а, если существует такое число М>0, чтоf(x)<Mвблизи точки х = а.

Теорема 7.Если функция f(x) имеет конечный предел при ха, то она ограничена вблизи точки х = а.

Доказательство.Пусть, т.е., тогда

или

, т.е.

где М =+А

Теорема доказана.

Бесконечно малые функции.

Определение.Функцияf(x) называетсябесконечно малойпри ха, где а может быть числом или одной из величин, +или -, если .

Бесконечно малой функция может быть только если указать к какому числу стремится аргумент х. При различных значениях а функция может быть бесконечно малой или нет.

Пример.Функцияf(x) =xⁿявляется бесконечно малой при х0 и не является бесконечно малой при х1, т.к. .

Теорема.Для того, чтобы функция f(x) при ха имела предел, равный А, необходимо и достаточно, чтобы вблизи точки х = а выполнялось условие

f(x) = A + (x),

где (х) – бесконечно малая при х  а ((х)0 при х  а).

Свойства бесконечно малых функций:

1. Сумма фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.

2. Произведение фиксированного числа бесконечно малых функций при ха тоже бесконечно малая функция при ха.

3. Произведение бесконечно малой функции на функцию, ограниченную вблизи точки х = а является бесконечно малой функцией при ха.

4. Частное от деления бесконечно малой функции на функцию, предел которой не равен нулю есть величина бесконечно малая.

Используя понятие бесконечно малых функций, приведем доказательство некоторых теорем о пределах, приведенных выше.

Доказательство теоремы 2.Представимf(x) =A+(x),g(x) =B+(x), где

, тогда

f(x)  g(x) = (A + B) + (x) + (x)

A+B=const,(х) +(х) – бесконечно малая, значит

Теорема доказана.

Доказательство теоремы 3.Представимf(x) =A+(x),g(x) =B+(x), где

, тогда

AB=const,(х) и(х) – бесконечно малые, значит

Теорема доказана.