2.9 Построение графиков зависимостей

Определим значения функций в крайних точках.

t = 0

i (0) = 0

u_c (0) = 0

u_L (0) = E

t = ∞

i _пр = 0

u_{c пр} = Е

u_{L пр} = 0

Кривая тока в начальный момент и в конце процесса равен нулю. При этом в начале процесса производная тока не равна нулю, так как

.

В середине процесса ток имеет максимум, совпадающий с переходом напряжения на индуктивности через нуль (t = t₁).

Скорость изменения напряжения на конденсаторе в начале процесса равна нулю

.

Это значит, кривая изменения напряжения на конденсаторе имеет точку перегиба в точке перехода напряжения на индуктивности через нуль, так как в этой точке

В интервале времени до t₁ ток возрастает, а индуктивность препятствует этому и напряжение на нем имеет положительное направление. После этого момента ток начинает уменьшаться и напряжение на индуктивности меняет свой знак. Отрицательный максимум напряжения совпадает с точкой перегиба кривой тока (t = t₂)

.

Кривые изменений тока, напряжения на емкости и индуктивности изображены на рис. 1.8 .

Рис. 1.8

Рассмотрим случай колебательного процесса. Здесь , или

и . (1.43)

Преобразуем выражение для корней:

.

Введем обозначение . Тогда

Для нахождения законов изменения при комплексно сопряженных корнях необходимо обратится к формулам Эйлера:

Из этих формул вытекает следующее:

, .

Преобразуем выражение для тока с использованием формулы Эйлера:

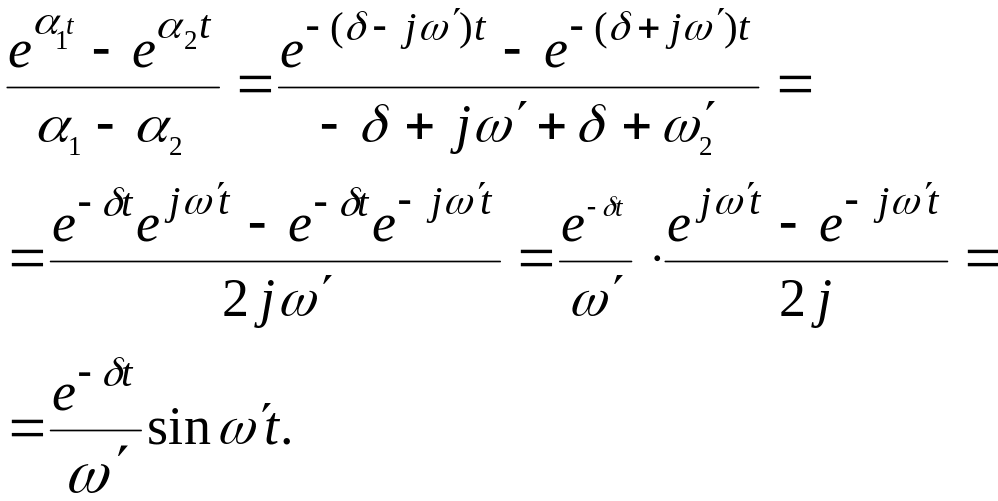
Итак

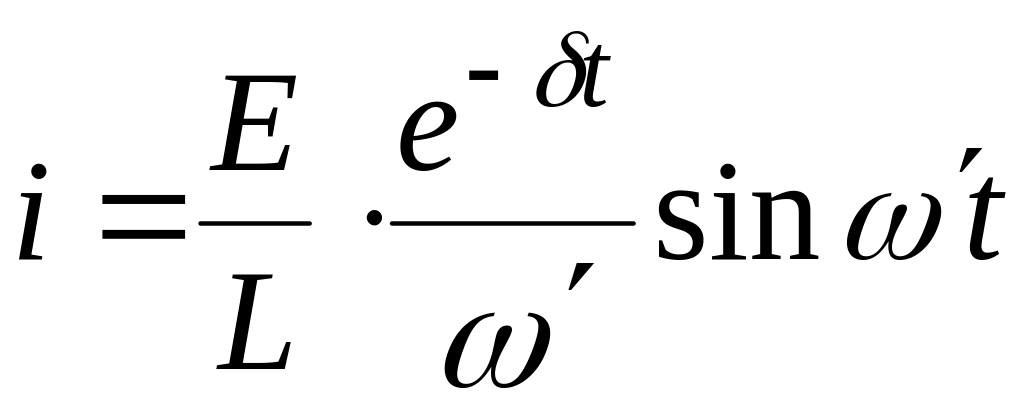. (1.46)

Аналогичным способом можно определить другие законы изменения. Имеется всего три конструкции, которые дают формулы перехода к колебательным функциям.

, (1.47)

, (1.48)

, (1.49)

где ;

;

С учетом изложенного выше, можно записать окончательно:

, (1.50)

, (1.51)

. (1.52)

Это затухающие синусоиды, графическое изображение которых приведено на рис. 1.9.

Рис. 1.9

В зависимости от параметров цепей синусоиды могут быть различными (рис. 1.10, а. б ) Такие затухающие синусоиды характеризуют с помощью декремента колебания. Декремент – отношение двух соседних максимумов кривой (см. рис. 1.9).

а)

б )

Рис. 1.10

. (1.53)

Но , тогда

. (1.54)

Величина называется логарифмическим декрементом колебания