3.9 Переход от изображений к оригиналам

После определения операторных выражений неизвестных необходимо найти оригиналы функций. Для этого есть два пути. Первый это нахождение оригиналов по таблицам. Второй путь – по теореме разложения.

Изображение тока в любой физически осуществимой цепи можно привести к виду:

. (2.25)

В этом выражении m ≤ n ; a_{k ,} b_k – вещественные числа; многочлены G(p), F(p) не имеют общих корней, т.е. дробь является несократимой. Кроме того, многочлен F(p) не имеет нулевых и кратных корней.

Известно, что дробь G(p)/ F(p) можно разложить на простейшие дроби:

, (2.26)

где р₁ , р_2, …р_к … р_n – корни знаменателя;

A₁ , A₂ , …A_k … A_n – коэффициенты, которые подлежат определению.

Обе части уравнения (2.26) умножим на р - р_к :

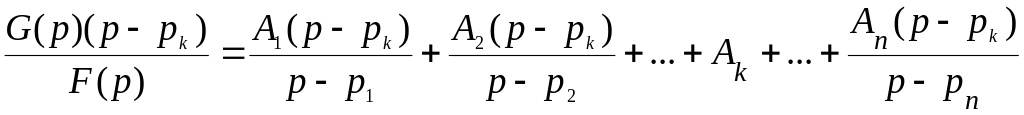
Пусть р → р_к , тогда р - р_к = 0 , и

.

В этом выражении правая часть содержит неопределенность, так как F(p) → 0 и р - р_к = 0. Эта неопределенность раскрывается по правилу Лопиталя.

,

Окончательно

, (2.27)

где F’(p) – производная.

. (2.28)

Так как

, (2.29)

то . (2.30)

Это есть теорема разложения. Правая часть полученного выражения представляет собой сумму экспоненциальных составляющих. Количество их равно числу корней знаменателя. Если знаменатель имеет нулевой корень, его можно представить в виде

.

В этом случае теорема разложения принимает вид:

. (2.31)

Рассмотрим несколько конкретных примеров. Включение конденсатора на постоянное напряжение (рис. 2.4).

Составим уравнение по второму закону Кирхгофа:

(2.32)

Перейдем к операторной форме записи:

. (2.33)

Откуда выражаем

. (2.34)

Упростим это уравнение:

. (2.35)

Введем обозначения в соответствии с теоремой разложения:

G(p) = С[E-u(0)] ,

F(p) = pCR – 1 = 0,

F’(p) = CR ,

P₁ = – 1/ CR.

Применим теорему разложения:

. (2.36)

При нулевых начальных условиях:

. (2.37)

Полученные выражения полностью совпадают с выражениями, полученными в классическом методе.

Для определения операторного выражения напряжения конденсатора запишем дифференциальное уравнение:

. (2.38)

Перейдем в операторную форму с учетом правила дифференцирования:

. (2.39)

При нулевых начальных условиях, после некоторых преобразований получаем

. (2.40)

В знаменателе этого выражения имеется нулевой корень. Следовательно, здесь требуется применение второй формы теоремы разложения:

. (2.41)

Т.е: . (2.42)

Последнее выражение также совпадает с классическим методом. Приведенные выше операторные выражения можно получить непосредственно по операторной схеме (рис. 2.5) используя методы цепей постоянного тока, например по закону Ома.