12.Матричный метод решения систем.

Систему

в матричном виде: АХ=В, где А ее квадратная матрица, Х - матрица-столбец из неизвестных, В - матрица-столбец из свободных членов системы.

Будем смотреть на АХ=В как на матричное уравнение, в котором неизвестна матрица Х. Покажем, что это уравнение имеет единственное решение, если матрица А является неособенной.

Действительно, неособенная матрица имеет обратную А^-1. Умножим обе части уравнения АХ=В на А^-1. Получим А^-1*(АХ)=А^-1*В. Т.к. произведение матриц ассоциативно, то (А^-1*А)*Х=А^-1*В или ЕХ=А^-1*В. Поскольку ЕХ=Х, то Х=А^-1*В, т.е. Х выражается через обращение матрицы А и матрицу В. Т.к. обратная матрица единственна, то и решение АХ=В единственно.

Т.о. имеем матричный способ решения (1) системы, который можно сформулировать в виде теоремы: Если матрица системы (1) неособенная, то система имеет единственное решение, которое представимо в матричном виде: Х=А^-1*В.

Алгоритм: Вычислить определитель Δ(А) системы. Если он не равен нулю то матрица А системы - неособенная и имеет единственную обратную А^-1. Находим ее. Для этого сначала вычисляются все алгебраические дополнения элементов матрицы А(А11=М11, А12= -М12).По формуле согласно правилам умножения матриц и умножения матрицы на число получаем неизвестную матрицу Х.

13.Ранг матрицы, теоремы о ранге.

Выберем в матрице А =aij размерности m n произвольные к строк и к столбцов, где 1 ≤ к ≤ min {m, n}. Определитель к-го порядка, составленный из элементов этой матрицы, расположенных на пересечении выделенных к строк и к столбцов, называется минором Мк к-го порядка матрицы А.

Минорами первого порядка являются сами элементы матрицы А, а их число равно mn. Если матрица нулевая, то все ее возможные миноры равны нулю.

Если все миноры некоторого порядка данной матрицы А равны нулю, то равны нулю и все миноры более высоких порядков.

Рангом матрицы называется наивысший порядок отличных от нуля миноров, то данное определение не позволяет говорить о ее ранге. По определению полагают, что ранг нулевой матрицы равен нулю. Если матрица имеет хотя бы один отличный от нуля элемент, то r ≥ 1. Тогда ясно, что только нулевая матрица имеет ранг, равный нулю.

Пусть Мк – главный (угловой) минор матрицы А порядка к. Любой минор (к + 1)-го порядка вида

М (k+1)=

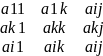
получающийся из Мк добавлением элементов i-й строки и j-го столбца, называется окаймляющим для минора Мк.

Справедлива теорема: если какой-нибудь угловой минор r-го порядка матрицы А отличен от нуля, а все миноры (r + 1)-го порядка, его окаймляющие, равны нулю, то ранг матрицы равен r. Из этой теоремы получаем следующий способ вычисления ранга матрицы: при вычислении ранга следует переходить от миноров меньших порядков к минорам высших порядков; если при этом окажется, что какой-то минор Мr отличен от нуля, а все окаймляющие миноры Мк+1 равны нулю, то ранг матрицы равен r.

Элементарными преобразованиями матрицы называются следующие преобразования:

1) перестановка местами любых двух строк;

2) умножение любой строки на произвольное отличное от нуля число;

3) прибавление к любой строке всякой другой строки, умноженное на не- которое число;

4) аналогичные преобразования столбцов матрицы.

Справедлива теорема: при элементарных преобразованиях матрицы ее ранг не изменяется. Тогда при вычислении ранга матрицы можно исключить из рассмотрения (вычеркнуть, отбросить):

1) нулевые строки;

2) одну из двух равных строк;

3) одну из двух пропорциональных строк;

4) строку, являющуюся линейной комбинацией остальных строк.

Обычно, отбрасывая нулевые строки и столбцы, матрицу А = (аij) приводят к трапецоидальной форме или треугольной форме, если все элементы b11, b22, …, brr этих двух матриц отличны от нуля, то их ранги равны числу r.