16.Системы с базисом. Приведение системы к системе с базисом методом Жордана-Гаусса.

Базисным решением системы называется всякое ее решение, в котором свободные переменные равны нулю.

При большом числе уравнений вычисление ранга матрицы системы (и ранговых миноров) достаточно трудоемкая задача. Обычно таких вычислений не проводят, и метод Жордана-Гаусса применяют не посредственно к рассматриваемой системе. Очевидным образом найдутся ранги матрицы системы и расширенной матрицы.

1. Если в результате выполнения итераций преобразованная система будет содержать уравнение 0*х1(вниз)+...+0*хn(вниз)=b, то она противоречива (противоречива и исходная система); ясно, что в этой ситуации r(A) ≠ r(Ā с черт).

2. Если преобразованная система будет иметь уравнения вида 0*х1(вниз)+...+0*хn(вниз)=0, то их надо отбросить, так как они являются следствиями остальных; ранг расширенной матрицы будет меньше числа min {m, n} на число исключенных из системы уравнений.

Алгоритм приведения системы к системе с базисом

1. Составляется таблица Гаусса.

2. Выбирается разрешающий элемент аsk ≠ 0. Тогда s-я строка называется разрешающей, а к-й столбец – разрешающим столбцом.

3. Элементы разрешающей строки делятся на разрешающий элемент, т.е. преобразуются по формуле

asj’= 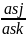(j=1,…,n)

Коэффициент при хк в s-ом уравнении преобразованной системы будет равен единице.

4. Элементы разрешающего столбца преобразованной таблицы аsk* = 1, заполняются нулями.

5. Элементы остальных строк преобразованной таблицы вычисляются по правилу прямоугольника.

Процесс метода Жордана-Гаусса продолжается, пока хотя бы в одной строке есть коэффициенты при неизвестных, отличные от нуля и не занимающие места разрешающих элементов предыдущих итераций.

17. Канонические системы. Преобразование однократного замещения.

Система с базисом, у которой свободные члены всех уравнений неотрицательны, называется канонической системой уравнений.

Чтобы найти какое-нибудь другое опорное решение канонической системы, надо перейти к другой канонической системе, равносильной исходной.

Приведем теорему о возможности перехода от одной канонической системы к эквивалентной канонической системе: если в канонической системе уравнений среди коэффициентов при каком-либо свободном неизвестном имеется хотя бы один положительный, то возможен переход к новой канонической системе. Эквивалентной исходной, в которой указанное свободное неизвестное окажется базисным.

Переход от одной канонической системы к равносильной канонической системе называется преобразованием (операцией) однократного замещения.

Алгоритм преобразования однократного замещения

1. По данной канонической системе заполняется таблица Жордана-Гаусса с добавлением двух столбцов – столбца из базисных неизвестных и вспомогательного столбца θ.

2. Выбирается разрешающий столбец. Это – любой столбец из коэффициентов при свободных неизвестных, имеющий хотя бы один положительный элемент.

3. Заполняется столбец θ. Для этого элементы свободного столбца (правые части системы) делятся на элементы разрешающего столбца.

4. Выбирается разрешающая строка. Это есть строка, против которой в столбце θ стоит наименьшее неотрицательное число.

5. Выбирается разрешающий элемент, которым является элемент, находящийся на пересечении разрешающей строки и разрешающего столбца.

6. Заполняется новая таблица по алгоритму привидения системы к системе с

базисом.