§2. Перетин прямих ліній і площин.

Подальша ілюстрація методу координат. Знаходження точки перетину двох прямих на площині еквівалентно розв’язанню системи з двох лінійних рівнянь. Виведення правила Крамера з введенням поняття визначника другого порядку. Знаходження точки перетину трьох площин в просторі еквівалентно розв’язанню системи з трьох лінійних рівнянь. Виведення правила Крамера з введенням поняття визначника третього порядку. Особливі випадки, пов’язані з параметричним методом розв’язання систем лінійних рівнянь: знаходження точки перетину двох прямих на площині, одна з прямих задана канонічним рівнянням; знаходження точки перетину прямої і площини в просторі, пряма задана канонічним рівнянням.

Пряма лінія є однією з базових, первісних геометричних фігур. В евклідовій геометрії, законам якої підпорядкований наш світ у не дуже великих масштабах, скажімо, у земних, через кожну точку можна провести пряму лінію. В просторі для двох прямих ліній можуть мати місце три ситуації: дві прямі лінії можуть перетинатися, бути паралельними і бути мимобіжними. Алгебраїчний критерій того, що дві просторові прямі перетинаються або є мимобіжними буде даний в §7. Там же буде розв’язана задача про знаходження пари найближчих точок на мимобіжних прямих. В цьому параграфі ми розв’яжемо задачу аналітичного знаходження точки перетину двох прямих ліній на площині трьох площин в просторі. Це означає знаходження координат точки перетину за рівняннями прямих ліній і площин. Оскільки пряма лінія і площина можуть бути задані лінійним рівнянням, то знаходження координат точки перетину зводиться до розв’язання системи лінійних рівнянь (далі – СЛР). Тут природнім чином з’являється поняття визначника 2-го і 3-го порядків (важливо, що саме так це поняття з’явилось історично).

2.1. Знаходження точки перетину двох прямих ліній на площині.

Нехай маємо дві прямі лінії, які задані рівняннями:

Припустимо, що ці прямі не паралельні. В §1 встановлено, що умовою паралельності прямих є пропорційність відповідних коефіцієнтів при змінних. Отже, нехай коефіцієнти не пропорційні. Тоді ці прямі неодмінно мають точку перетину, і до того ж тільки одну. Це, так би мовити, принципова геометрична інформація. Далі виконуємо аналітичну роботу: знаходимо координати точки перетину. Для цього треба розв’язати СЛР:

Якщо перше рівняння помножити на , друге помножити на і від першого відняти друге, у формальному запису

,

то коефіцієнт при буде рівний 0, тобто змінна буде виключена, утвориться рівняння від однієї змінної :

,

звідки

.

Виключивши подібним чином змінну (пояснити, як саме: вказати відповідне перетворення), отримаємо:

,

звідки

.

Придивимось уважно до отриманих формул, які визначають значення координати точки перетину. Ми побачимо, що вирази у чисельниках і знаменниках утворені за однаковою алгебраїчною схемою:

,

,

.

Таблиця

називається матрицею розмірів 2х2 (або квадратною матрицею порядку 2), а число, обчислене за правилом: ліве верхнє число помножити на праве нижнє число мінус праве верхнє число помножити на ліве нижнє число, – називається визначником (або детермінантом) цієї матриці, точніше, визначником другого порядку. Відповідний вираз – він же є визначник – має своє позначення:

.

Таким чином, маємо формули:

, .

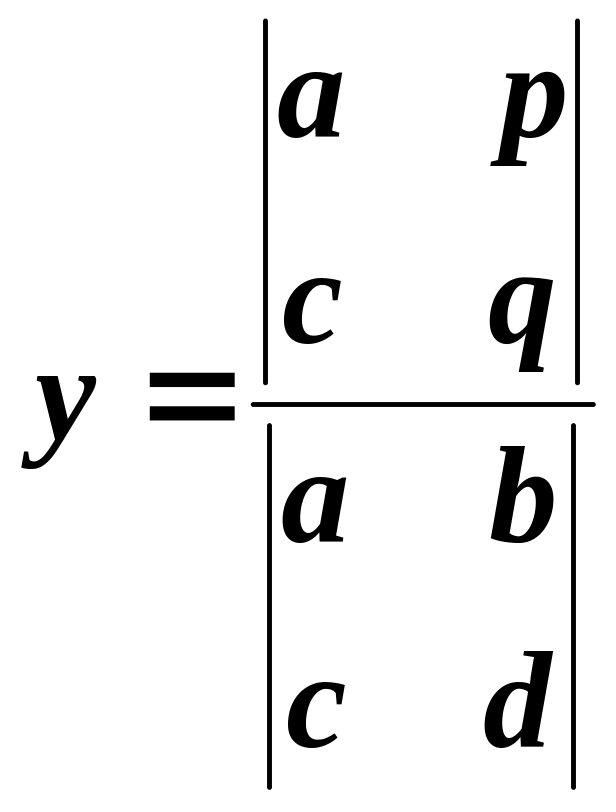Стосовно розглядуваної задачі знаходження розв’язку СЛР використовується спеціальна термінологія і позначення:

– основний визначник (складений з коефіцієнтів при змінних);

– допоміжний визначник – чисельник дробу для обчислення ;

– допоміжний визначник – чисельник дробу для обчислення .

Таким чином, доведена

Теорема Крамера для СЛР 2х2. Якщо основний визначник СЛР

відмінний від нуля, то СЛР має, і до того ж єдиний, розв’язок, який знаходиться за формулами (правилом) Крамера:

, .

Приклад. Знайдемо точку перетину двох прямих і . Задача зводиться до розв’язання СЛР

Увага: формули Крамера виведені для такого запису СЛР, у якому вільні члени знаходяться в правих частинах СЛР. Виконаємо потрібне перетворення:

Тепер усе готове до застосування правила Крамера.

Порада: для людей з не дуже великим практичним математичним досвідом дуже корисним буде супроводжувати аналітичні перетворення геометричними ескізами. От, наприклад, попереднє зауваження. Раптом людина забула перенести у рівняннях прямих вільні члени у праві частини (автор багато-багато разів спостерігав це явище), – тоді (при подальших правильних діях) вона отримає числа, протилежні за знаком істинним координатам точки перетину прямих. Навіть нашвидкуруч виконаний малюнок застереже від принципової помилки:

≠ 0 (не важливо, додатнє значення має визначник чи від’ємне, аби не нульове) правило Крамера можна застосовувати.

,

,

, .

Знайдені значення координат точки перетину прямих не протирічать малюнку. Робимо аналітичну перевірку:

Остаточно: точка перетину прямих .