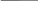1. Графы, сети и их применение в экономике

Появление теории графов связано с именем выдающегося математика, члена Петербургской академии наук Леонарда Эйлера. Он часто бывал в Кенигсберге, где четыре района города были соединены семью мостами. Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по всем мостам, не проходя ни по одному из них дважды? Многие кёнигсбергцы пытались решить эту задачу, как теоретически, так и практически, во время прогулок. Но никому это не удавалось, однако не удавалось и доказать, что это даже теоретически невозможно.

В 1736 году задача о семи мостах заинтересовала Леонарда Эйлера. Он и доказал, что невозможно пройти по всем мостам, не проходя ни по одному из них дважды.

2.1. Основные определения и характеристики графов.

Плоские графы

В разделе надо уделить внимание определениям и способам задания графов, включая матричные. Этот раздел должен заложить основу понимания всего последующего материала.

Пусть дано непустое множество X, состоящее из элементов, называемых точками (x₁,x₂,…,x_n) и нa X задано множество отношений Т, позволяющих установить соответствие между каждым элементом множества X и некоторым его подмножеством. Каждая пара точек х_i, x_j множества X, между которыми установлено отношение из множества Т, называется ребром.

Определение 2.1. Непустое множество X и множество отношений Т на­зываются графом, который обозначается G(X,T). Граф называется конечным, если множество X конечно.

С геометрической точки зрения граф G(X,T) представляет собой непустое множество точек (вершин) и множество отрезков (ребер), концы которых принадлежат данному множеству точек. При изображении графов ребра могут быть прямолинейны или криволинейны, длины ребер и расположение вершин произвольны. На рис. 2.1, а-в изображен один и тот же граф.

а	б	в
Рис. 2.1

Ребра графа обозначают парой вершин (x₁, x₂).

Вершины, не принадлежащие ни одному ребру графа, называются изолиро­ванными.

Рассмотрим граф (рис. 2.2). Вершины х₁, х₄, х₅ изолированные (они не принадлежат графу).

Граф может не иметь ребер. Тогда он состоит из изолированных точек.

x4 x1 x5	x4 x3 x2 x1
Рис. 2.2	Рис. 2.3

Граф, изображенный на рис. 2.3, состоит только из изолированных точек.

Две вершины называются смежными, если они соединены ребром, два ребра смежные, если они имеют общую вершину.

Ребро и любая из его вершин называются инцидентными.

Ребро графа G(X.T), у которого началь­ная и конечная вершины совпадают, называ­ется петлей.

Рассмотрим граф (Рис. 2.4). Ребро (х₄, х₄) является петлей.

x₄

x₃

x₂

x₁

Рис. 2.4

Примерами графов могут служить схемы железных и автомобильных дорог, метрополитена, формулы молекул, генеалогические деревья и т. д.

Существуют различные способы задания конечного графа G(X, T). Пусть x₁,x₂,…,x_n − вершины графа, l₁, l₂,…,l_m —ребра графа.

Определение 2.2. Матрицей смежности называется матрица А_m×n, в которой элемент а_ij равен количеству ребер, соединяющих вершины х_i и х_j.

Определение 2.3. Матрицей инцидентности называется матрица В_n×m, в которой элемент b_ij равен 1, если вершина х_i, инцидентна ребру l_j, и равен 0 в противном случае.

Пример 2.1. Для графа на рис. 2.5 матрица смежности А и матрица инцидентности В имеют вид

0 1 0 0 0 0 1 0 0 0 0 0 0 0

1 0 1 1 1 0 1 1 0 1 0 1 0 0

0 1 0 0 1 0 0 1 1 0 0 0 0 0

А = 0 1 0 0 1 0 В = 0 0 0 1 1 0 0 0

0 1 1 1 0 1 0 0 1 0 1 1 1 0

0 0 0 0 1 1 0 0 0 0 0 0 1 1

Кроме того, графы можно задавать списками пар вершин, соединенных ребрами, или заданием для каждой вершины множества смежных вершин.

Полным графом G(X,T) называется граф, в котором для каждой пары вершин х_i, х_j существует ребро, инцидентное х_i и инцидентное х_j (каждая вершина соединена ребром с любой другой вершиной)

l3 l2 x6 x3 x5 x2 x1 l6 l8 l7 l5 l4 l1 x4
Рис. 2.5	Рис. 2.6

Граф, изображенный на рис. 2.6, является полным.

В полном графе каждая вершина принадлежит одному и тому же числу ребер, так как она соединена со всеми остальными вершинами. Для задания полного графа достаточно знать число его вершин. Неполный граф можно преобразовать в полный с теми же вершинами, добавив недостающие ребра.

Дополнением графа G(X,T) называется граф G(X,T) с теми же вершинами, что и граф G(X,T), и теми ребрами, которые необходимо добавить к графу G(X,T), чтобы получился полный граф.

Граф G(X,T) (Рис.2.7, а) – неполный. Полный граф (Рис. 2.7, б) получается из графа G(X,T) с помощью дополнения (показано штриховыми линиями).

а	б
Рис. 2.7

Степенью вершины x_i графа G(X,T) называется число d_i, равное коли­честву ребер графа, инцидентных этой вершине. Вершина называется четной (нечетной), если ее степень — четное (нечетное) число.

Определение 2.4. Путем от x_i до x_j называется такая последовательность ребер графа, ведущая от x_i к x_j , в которой два соседних ребра имеют общую вершину и никакое ребро не встречается дважды. Длиной пути называется число ребер этого пути.

Путь от x_i до x_j называется простым, если он не проходит через одну вершину более одного раза.

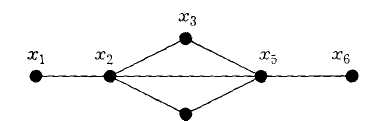
Пример 2.2. Рассмотрим граф (рис. 2.8).

x₄

Рис. 2.8

В данном графе есть следующие пути от х₁ до х₆:

x₁, х₂,х₅,х₆ — путь длиной 3;

x₁,x₂,x₃,x₅,x₆ — путь длиной 4;

x₁,x₂,x₄,x₅,x₆ — путь длиной 4;

x₁,x₂,x₃,x₅, x₄, x₂,x₅,x₆ — путь длиной 7;

x₁,x₂, x₄, x₅, x₃,x₂,x₅,x₆ — путь длиной 7.

Первые три пути являются простыми.

Циклом называется путь, в котором начальная и конечная вершины совпадают; длиной цикла — число ребер в этом цикле.

Цикл называется простым, если он не проходит через одну вершину более одного раза.

Пример 2.3. Рассмотрим граф, приведенный на рис. 2.9. В этом графе есть несколько циклов, которые частично перечислены на рис. 2.9.

	x1, х5,х4, х1 — цикл длиной 3; x1, х2,х3, х1 — цикл длиной 3; x1, х2,х4, х5,х3, х1 — цикл длиной 5; x1, х2,х4, х5, х2, х3, х1 — цикл длиной 6; и т. д. Первые три цикла простые.
Рис.2.9

Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах, и несвязными в противном случае.

Граф называется связным, если любые две его вершины связны, и несвязным в противном случае.

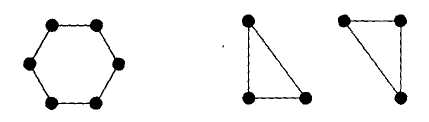
Пример 2.4. В группе из шести человек каждый знаком с двумя и только с двумя другими. Вариантов такой группы может быть два: в первом (рис. 2.10, а) мы имеем связный граф, во втором (рис. 2.10,б) — несвязный.

а

б

Рис. 2.10

Определение 2.5. Ребро (х_i, x_j) называется мостом, если в графе G(X, Т), полученном после удаления ребра (х_i, x_j), вершины х_i и x_j несвязны.

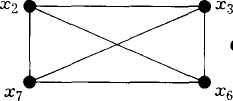
Рассмотрим граф на рис. 2.11. а. В этом графе ребро (х₃, х₅) является мостом, поскольку в графе, полученном после удаления данного ребра (рис. 2.11,б), вершины х₃ и х₅ несвязны.

X₁

X₁

X2 X6 X3 а X7 X5 X4	X2 X6 X3 б X7 X5 X4
Рис. 2.11

Существует несколько признаков мостов:

ребро (х_i, x_j) является мостом тогда и только тогда, когда (х_i, x_j) единственным путем, соединяющим вершины х_i и x_j;

ребро (х_i, x_j) является мостом тогда и только тогда, когда найдутся две вершины х_k и x_m, такие, что любой путь, соединяющий их, содержит вершины х_i и x_j;

ребро (х_i, x_j) является мостом тогда и только тогда, когда оно не принадле­жит ни одному циклу.

Связный граф без циклов называется деревом. Вершина дерева, имеющая степень 1, называется висячей. По аналогии с генеалогическими деревьями вводятся родовые понятия для вершин. Рассмотрим граф (рис. 2.12).

X₉

Рис. 2.12

В этом графе вершина х₁ называется кор­невой, а пути от нее — ветвями. Вершина х₂ называется родительской по отношению к вершинам х₄, х₅, х₆ и прародительской по от­ношению к вершинам x₈, x_8. Вершины х₂ и х₃ называются дочерними по отношению к вершине х₁.

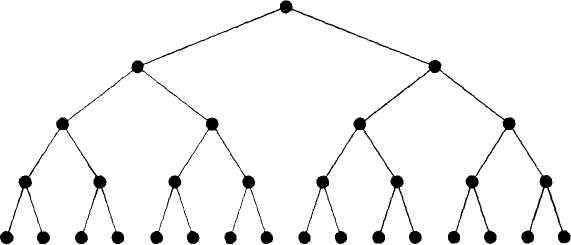
Пример 2.5. Кубок по настольному теннису разыгрывают 16 команд по олимпийской системе. Схему турнира можно изобразить деревом (Рис. 2.13).

Рис. 2.13

Любое ребро в дереве является мостом. Для каждой пары вершин дерева существует единственный соединяющий их путь.

Как мы уже говорили, один и тот же граф может быть изображен по-разному. Для того чтобы узнать, совпадают ли графы, необходимо предварительно проверить следующие условия:

одинаковое ли число вершин в графах;

одинаковое ли число ребер в графах;

одинаковое ли число вершин в графах имеют степень k.

Необходимым и достаточным условием совпадения графов является суще­ствование такого взаимно однозначного соответствия между ними, при котором две вершины в одном графе соединены ребром тогда и только тогда, когда со­единены ребром соответствующие вершины в другом графе.

Плоские графы

Определение 2.6. Граф G(X,T) называется плоским, если его можно изобразить на плоскости так, чтобы никакие два его ребра не имели других общих точек, кроме их общей вершины. Чертеж графа, на котором никакие два ребра не пересекаются, называют плоским представлением графа.

Примерами плоских графов могут служить простые циклы, деревья, лес и т. д.

Дан граф (рис. 2.14, а). Его плоским представлением является граф, изобра­женный на рис. 2.14, б.

Плоское представление имеет только плоский граф, и обратно: у всякого плоского графа всегда найдется плоское представление.

Рис. 2.14

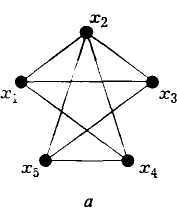
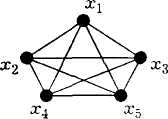
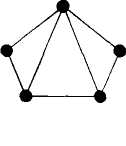
В качестве примера неплоского графа можно привести полный граф с пятью вершинами (рис. 2.15).

Рис.2.15

Любые попытки начертить его плоское представ­ление обречены на неудачу.

Гранью в плоском представлении графа G(X.T) называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов. Часть плоскости, расположенная вне плоского представления графа и ограниченная изнутри простым циклом, называется бесконечной гранью.

Две грани называются соседними, если их границы имеют хотя бы одно общее ребро.

Граф, представленный на рис. 2.16, имеет четыре обычные грани, ограничен­ные циклами ( х₁, х₂, х₆, х₁), ( х₅, х₆ х₇, х₅), (х₂, х₃, х₄, х₅, х₂), (х₂, х₅, х₇, х₆, х₂) и одну бесконечную грань, ограниченную циклом (х₁, х₂, х₃, х₄, х₅, х₆, х₁).

Грани ( х₁, х₂, х₆, х₁) и (х₂, х₅, х₇, х₆, х₂) соседние, а грани ( х₁, х₂, х₆, х₁) и (х₂, х₃, х₄, х₅, х₂) соседними не являются. Часть плоскости, ограничен­ная простым циклом (х₂, х₅, х₆, х₂) не признается гранью, так как содержит внутри себя цикл ( х₅, х₆ х₇, х₅).

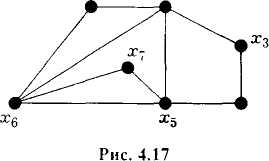
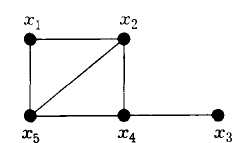
В графе, показанном на рис. 2.17, часть плоскости, ограниченная простым циклом (х₁, х₂, х₃, х₄,х₁), считается гранью, поскольку ребро (х₁, х₅), рас­положенное внутри грани, не является циклом.

x4 x2 x1
Рис. 2.16	Рис. 2.17	Рис. 2.18

Рассмотрим граф, изображенный на Рис. 2.18. Часть плоскости, заключенная между циклами (х₁, х₂, х₃, х₄, х₅, х₁) и (х₆ х₇, х₈, х₆), не является гранью, так как содержит внутри себя цикл и к тому же не ограничена циклом. Ребро (х₁, х₆) − мост, соединяющий два цикла.

Мост, соединяющий два цикла, называется перегородкой.

Граф, изображенный на рис. 2.19, не имеет бесконечной грани, поскольку она не ограничена изнутри простым циклом. Мост (х₁, х₂) явля­ется перегородкой. В плоском представлении дерева за грань при­нимают всю плоскость чертежа. Для всякого плоского графа без перегородок число вершин n, число ребер m и число граней с учетом бесконечной g связаны соотношением n − m + g = 2, которое называется формулой Эйлера.

Операция добавления новых ребер, в результате которой в плоском представлении графа каждая грань имеет три вершины, называется триангуляцией графа.

Плоский граф G(X,T) называется максимально плоским, или триангулирован­ным, если к нему невозможно добавить ни одного ребра так, чтобы полученный граф был плоским.

	а	б
Рис. 2.19	Рис. 2.20

Рассмотрим граф (рис. 2.20, а). Этот граф можно сделать максимально плоским (рис. 2.20, б). Каждая грань в плос­ком представлении максимально плоского графа имеет три вершины.

Эйлеровым путем в графе называется путь, содержащий все ребра графа и проходящий через каждое по одному разу.

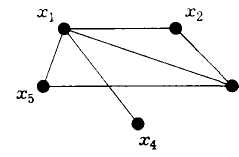
Рассмотрим граф (рис. 2.21). Он имеет эйлеров путь (х₄, х₁, х₃, х₂, х₁, х₅, х₃).

Эйлеровым циклом в графе называется цикл, содержащий все ребра графа и проходящий через каждое ребро по одному разу.

Граф, обладающий эйлеровым циклом, называется эйлеровым графом.

X3
Рис. 2.21	Рис. 2.22

Рассмотрим граф (рис. 2.22). Данный граф является эйлеровым, так как он имеет эйлеров цикл (х₂, х₅, х₄, х₁, х₂, х₃, х₄, х₂).

Гамильтоновым путем в графе называется путь, проходящий через каждую вершину графа в точности по одному разу.

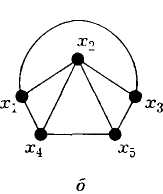
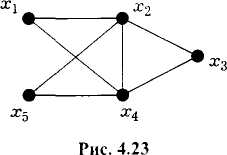
Например, граф на рис. 2.23 имеет гамильтоновы пути (х₃, х₄, х₅, х₁, х₂) и (х₃, х₄, х₂, х₅, х₁).

Гамильтоновым циклом в графе называется цикл, проходящий через каждую вершину графа в точности по одному разу.

Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом.

Рис. 2.23	Рис. 2.24

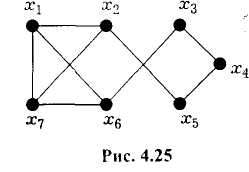
Граф, изображенный на рис.2. 24, является гамильтоновым, так как имеет гамильтоновы циклы (х₁, х₇, х₆, х₃, х₄, х₅, х₂, х₁) и (х₁, х₆, х₃, х₄, х₅, х₂, х₇, х₁).

Всякий полный граф является гамильтоновым, так как он содержит такой простой цикл, которому принадлежат все вершины графа.