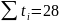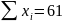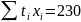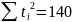- •Графы, сети и их применение в экономике
- •2.1. Основные определения и характеристики графов.
- •2.2. Ориентированные графы. Построение минимального остовного дерева сети
- •2.3. Задача нахождения кратчайшего пути. Дерево решений
- •2.4. Сетевые графики
- •Вопросы и задачи для самопроверки
- •5. Математические модели в финансовых операциях
- •5.1. Простые проценты. Сложные проценты
- •5.2. Начисление процентов в условиях инфляции.
- •5.3. Погашение кредита. Балансовое равенство
- •5.4. Балансовое уравнение
- •Иерархии и приоритеты
- •6.1. Приоритеты. Измерения и согласованность. Идеальные измерения
- •Первый состоит в том, чтобы определить (угадать) вес каждого предмета, взяв за единицу измерения (эталон) самый маленький, а значит и самый легкий. Это потребует (n – 1) сравнений.
- •6.2 Обратно-симметричные и согласованные матрицы. Индекс согласованности
- •6.3 Вычисление собственных характеристик обратно-симметричной матрицы
- •6.4 Проблема сравнения. Построение шкал. Иерархии
- •7. Методы прогнозирования
- •7.1 Анализ временных рядов. Метод подвижного (скользящего) среднего.
- •7.2 Метод проецирования тренда
- •7.3 Прогнозирование с учетом сезонной вариации. Аддитивная модель
- •7.4. Мультипликативная модель. Каузальные методы прогнозирования. Качественные методы прогнозирования
- •8. Основы управления рисками в экономике
- •8.1. Риски в экономике. Оптимизация портфелей банка
- •9. Динамические модели
- •9.1. Модель народонаселения
- •9.2. Модель мобилизации
- •9.3. Модель гонки вооружений
- •9.4. Модель хищник – жертва
7.2 Метод проецирования тренда
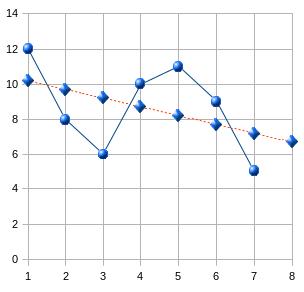
Основной идеей метода проецирования (линейного) тренда (trend projection) является построение прямой (в общем случае линии более высокого порядка), которая "в среднем" наименее уклоняется от массива точек (ti, xi), i = 1, 2,..., n, заданного временным рядом (рис. 7.9). Этот метод часто называют методом наименьших квадратов.
Эта прямая ищется в следующем виде:
x = at + b, (7.4)
где a и b – постоянные, подлежащие определению.
x = a t + b
a ti
+ b
t1
t2 t3
ti
tn
x
t |
Рис. 7.9 |
Чтобы найти коэффициенты a и b,поступают так: для каждого значения ti переменной t, пользуясь формулой (7.4) вычисляют соответствующее значение переменной х:
ati + b, i = 1, 2,..., n,
находят разность
ati + b − xi, i = 1, 2,..., n,
которую затем возводят в квадрат (чтобы не думать о знаке):
( ati + b − xi)2, i = 1, 2,..., n,
и, суммируя полученные разности по количеству точек, в итоге получают некоторую вспомогательную функцию, которую мы обозначим φ(a,b):
φ(a,b)
=
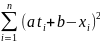 →min
(7.5)
→min
(7.5)
Требуется выяснить при каких a и b достигается минимум этой функции. Функция φ(a,b) принимает минимальное значение в том случае, когда величины a и b удовлетворяют следующей линейной системе:
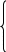
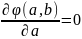
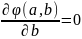
Находя частные производные, приходим к системе уравнений:
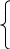
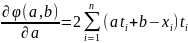 = 0
= 0
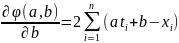 = 0
(7.6)
= 0
(7.6)
Систему
(7.6) можно
переписать иначе, сгруппировав переменные
под знаками суммы и перенеся суммы,
содержащие
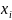 ,
в правую часть уравнений:
,
в правую часть уравнений:
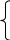 a
a
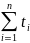 + bn =
+ bn =
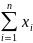 ,
,
a
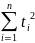 + b
=
+ b
=
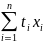 .
(7.7)
.
(7.7)
Эта система всегда имеет единственное решение. Уравнения (7.7) называются также нормальными уравнениями.
Решая систему уравнений (7.7), например методом Гаусса, приходим к выражениям для а и b:
-
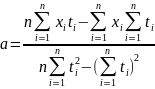

(7.8)
Можно указать простой и общий способ составления нормальных уравнений. Используя опытные точки и уравнение (7.4), можно записать систему уравнений для a и b:
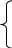 x1=
at1
+ b
x1=
at1
+ b
x2= at2 + b
………….
|
Умножим левую и правую части каждого из этих уравнений на коэффициент при первой неизвестной a (т. е. на t1, t2, ..., tn) и сложим полученные уравнения, в результате получится второе нормальное уравнение из (7.7). Умножим левую и правую части каждого из этих уравнений на коэффициент при второй неизвестной b, т. е. на 1, и сложим полученные уравнения, в результате получится первое нормальное уравнение из (7.7). Этот способ получения нормальных уравнений является общим: он пригоден, например, и для функции
x = a0 + a1 t + a2 t2 + a3 t3 + …+ an tn.
Естественно, что здесь получится система из n+1 нормальных уравнений для определения величин a0, a1, a2, ..., an.
Рассмотрим конкретный пример, вновь обратившись к заданному временному ряду.
Составим вспомогательную таблицу (табл. 7.5):
Таблица 7.5 |
|||
ti |
xi |
ti xi |
ti2 |
1 |
12 |
12 |
1 |
2 |
8 |
16 |
4 |
3 |
6 |
18 |
9 |
4 |
10 |
40 |
16 |
5 |
11 |
55 |
25 |
6 |
9 |
54 |
36 |
7 |
5 |
35 |
49 |
|
|
|
|
В этом случае система уравнений (нормальные уравнения) для отыскания a и b записывается в следующем виде:
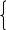 28а
+
7b
= 61
28а
+
7b
= 61
140а + 28b = 230. (7.9)
Решая систему, получаем:
a = − 14 / 28 = − 0,5; b = 300 / 28 10,7.
Тем самым х = − 0,5t + 10,7 – уравнение искомого тренда.
Нетрудно убедиться, что, подставив соответствующие значения сумм из вспомогательной таблицы в (7.8), значения для a и b получатся те же самые:
а
=
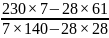 =
=
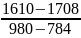 =
−
=
−
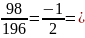 − 0,5;
− 0,5;
b
=
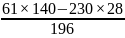 =
=
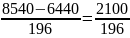 10,7.
10,7.
Таким образом, коэффициенты a и b можно получить, подставляя значения сумм в решение нормальных уравнений в общем виде (7.8), или составляя нормальные уравнения подобно (7.9) с численными множителями, т. е. значениями сумм из вспомогательной таблицы, при неизвестных a и b.
(см. рис. 7.10).
Замечание. Точность прогноза можно оценить при помощи стандартного отклонения или дисперсии. Стандартное отклонение определяется по формуле:
 .
(7.10)
.
(7.10)
Среднеквадратическое отклонение вычисляется по формуле:
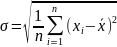 .
(7.11)
.
(7.11)
В этих формулах:
![]() −стандарт
или стандартное отклонение, несмещенная
оценка среднеквадратического отклонения
случайной величины X относительно её
математического ожидания;
−стандарт
или стандартное отклонение, несмещенная
оценка среднеквадратического отклонения
случайной величины X относительно её
математического ожидания;
![]() —
дисперсия;
—
дисперсия;
![]() −
i−й элемент выборки;
−
i−й элемент выборки;
![]() −
среднее арифметическое выборки;
−
среднее арифметическое выборки;
![]() —
объём выборки.
—
объём выборки.
Следует отметить отличие стандартного отклонения (в знаменателе стоит n −1) от корня из дисперсии (среднеквадратического отклонения) (в знаменателе − n). При малом объеме выборки оценка дисперсии через последнюю величину является несколько смещенной, при бесконечно большом объеме выборки разница между этими величинами исчезает.
Можно также точность прогноза оценить при помощи коэффициента корреляции:
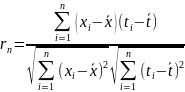 . (7.12)
. (7.12)
Если коэффициент корреляции rn =1, то xi = ati+b, если rn = −1, то xi=−ati+b. Таким образом, близость коэффициента корреляции к 1 (по абсолютной величине) говорит о достаточно тесной линейной связи.
|
Рис. 7.10 |
Замечание. Следует также отметить, что при построении прогноза методом проецирования тренда используется весь массив имеющихся данных, и, следовательно, можно ожидать при этом меньшей погрешности, чем в при построении прогнозов методами скользящей средней или экспоненциального сглаживания. Это утверждение справедливо только в том случае, если тенденция (тренд) не меняется на протяжении периода, когда были получены числовые данные для прогнозирования и есть уверенность, что тренд не изменится в прогнозируемом периоде. Метод проецирования тренда, однако, требует более сложных вычислений, чем первые три названных метода.