9.4. Модель хищник – жертва

В модели Мальтуса рассказывалось о беспрепятственном размножении популя­ции. Однако в реальных обстоятельствах популяция сосуществует с другими популяциями, находясь с ними в самых разных взаимо­отношениях.

Здесь мы коротко рассмотрим антагонистическую пару хищник - жертва (это может быть и пара рысь – заяц, лиса – кролик, и пара божья коровка − тля) и попытаемся проследить, как может изменяться со временем численность обеих взаимодействующих сторон.

Предполагаем, что популяция жертвы может существовать сама по себе, поскольку питается растительной пищей, в то время как популяция хищника существует только за счет жертвы.

Обозначим численность популяции жертвы через х, а численность популяции хищника – через у.

В отсутствие хищника жертва размножается согласно уже известному уравнению

= αх, α > 0,

а хищник в отсутствие жертвы вымирает по закону

= β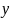 , β > 0.

Хищник съедает количество жертвы, пропорциональное ее собственной численности и численности хищника. Поэтому при наличии хищника численность жертвы меняется по закону

= α х γ xy, γ > 0.

Съеденное количество жертвы способствует размножению хищника, что можно записать так:

= − βу + δ ху, δ > 0.

Таким образом, мы получаем систему уравнений, которая носит имя модели Вольтерра-Лотки:

= αx γxy,

= βy + δxy, (9.24)

причем

0, 0,

Модель хищник – жертва построена.

Как и в предыдущей модели, наибольший интерес для нас представляет точка равновесия (х*, у*), где = 0 и = 0, а х* и у* представляют собой отличное от нуля решение системы уравнений:

αx γxy = 0

βy + δxy = 0,

или

x (α γ y) = 0, y( β + δ x) = 0. (9.25)

Координаты точки равновесия M*, являющейся точкой пересечения прямых

αx γxy = 0, (9.26)

βy + δxy = 0 (9.27)

легко вычисляются (рис. 9.11):

х*= β/δ, у*= α/γ.

Начало координат О (0,0) лежит в положительной полуплоскости относительно горизонтальной прямой, задаваемой уравнением (9.26), а относительно вертикальной прямой, задаваемой уравнением (9.27), − в отрицательной полуплоскости (рис. 9.12).

Первую четверть – а нас по-прежнему интересует только она, так как х 0 и у 0 – можно разбить, действуя аналогично только что изложенному, на четыре области, которые удобно обозначить так:

I – (+,+), II – (−,+), III – (−,−), IV – (+,−).

Пусть начальное состояние Q (х₀,у₀) находится в области IV. Тогда выполнены неравенства

α γ y₀ 0, β + δ x₀ 0,

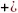
O β/δ α/γ M* y x	O I II IV III y x
Рис.9.11	Рис.9.12

из которых следует, что скорости и в этой точке должны иметь разные знаки

> 0, < 0,

и, значит, величина х должна возрастать, а величина y убывать.

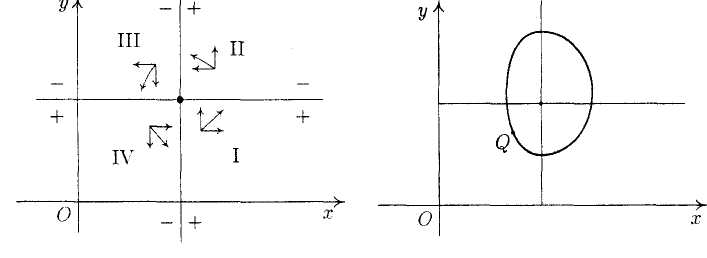
Подобным же образом анализируя поведение х и у в областях I, II и III, получим в итоге картину, изображенную на рис. 9.13.

Рис. 9.13 Рис. 9.14

Отклонение от состояния равновесия приводит к колебаниям численности жертвы и хищника вокруг точки равновесия (рис. 9.14). Так, если в некоторый момент времени система находится в точке Q, то с течением времени она опять вернется в эту точку, если на систему не будет оказано дополнительного воздействия.

Аналогичными уравнениями описывается поведение гармонического осциллятора. По аналогии с гармоническим осциллятором, поведение системы хищник – жертва не является структурно устойчивым. Небольшое изменение модели, например, учет ограниченности ресурсов, необходимых жертве, может привести к качественному изменению поведения системы. Может случиться, что равновесное состояние станет устойчивым, и колебания численности будут затухать. Возможен и противоположный сценарий, когда любое малое отклонение от положения равновесия приведет к катастрофическим последствиям, вплоть до полного вымирания одного из видов. Однако на вопрос о том, какой из этих сценариев реализуется, модель Вольтерра — Лотки ответа не дает: здесь требуются дополнительные исследования.

Следует упомянуть одну из современных экономических моделей – магистральную теорию, или магистраль. В математической экономике магистралью называется траектория экономического роста, на которой пропорции производственных показателей (такие как темп роста производства, темп снижения цен) неизменны, а сами показатели (такие как интенсивность производства, валовый выпуск) растут с постоянным максимально возможным темпом. Таким образом, магистраль - это траектория или луч максимального сбалансированного роста. Ее часто сравнивают со скоростной автострадой. Это образное сравнение принадлежит Дорфману, Самуэльсону и Солоу. Допустим, что некто хочет проехать по большому городу из пункта А в пункт Б. Если пункты А и Б расположены недалеко друг от друга, то скорее всего самый быстрый путь − это самый короткий. Однако если расстояние между А и Б велико, то самый быстрый путь оказывается чаще всего таким: надо из А выехать на одну из больших городских магистралей, где средняя скорость движения достаточно высока, не смущаясь тем, что мы, возможно, движемся в сторону от цели Б, по этой магистрали приблизиться, насколько возможно, к пункту Б и затем только с нее свернуть. Именно так возник научный термин "магистраль".

Поскольку "оптимальное" или "эффективное" развитие экономики в любом смысле так или иначе связано и должно сопровождаться экономическим ростом, то для достижения любой конечной цели следует поступать аналогичным образом: сначала вывести производство на магистральный путь, т. е. на так называемую траекторию (или луч) Неймана, характеризующуюся максимальным темпом роста 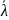и минимальной нормой процента 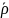= , а по истечении определенного срока времени вывести ее к задуманной цели. Такими целями могут быть максимизация прибыли, минимизация затрат, максимизация полезности от потребления товаров, достижение конкурентного равновесия при наиболее благоприятных условиях, т. е. на более высоком уровне благосостояния населения, и т. д.

Итак, с одной стороны мы имеем магистральные модели, а с другой − оптимизационные или еще шире − нормативные модели экономики. Изучение этих двух моделей во взаимосвязи, т. е. изучение связи между магистральными и оптимальными (в том или ином смысле) траекториями и является предметом магистральной теории. Можно говорить, что магистральная теория является одним из средств качественного анализа оптимальных траекторий.