2.4. Сетевые графики

Этот раздел представляет большой интерес для успешной профессиональной деятельности в будущем. Надо запомнить основные понятия, водимые в разделе и правила построения сетевых графиков.

До появления сетевых методов работы и проекты планировались в небольших объемах. Наиболее известным методом такого планирования был ленточный график Ганта. Недостаток этого метода заключался в том, что он не позволял установить зависимости между различными работами.

Современное сетевое планирование начинается с разбиения программы на конкретные работы. Оценивается продолжительность работ и строится сете­вая модель (график). Построение сетевой модели позволяет проанализировать все работы и внести улучшения в структуру модели до начала ее реализации

Составляется календарный график, определяющий начало и окончание каждой работы, а также взаимосвязи с другими работами. Календарный график вы­являет критические работы, которым нужно уделять особое внимание, чтобы закончить все работы в директивный срок. Для некритических работ календарный график позволяет установить резервы времени с целью эффективного использования трудовых и финансовых ресурсов.

Изучая раздел, нужно проследить решение приводимых примеров по шагам. По окончании работы с теоретическим материалом необходимо ответить на вопросы для самопроверки и на вопрос тренировочного теста.

1. Вопросы и задачи для самопроверки

   1. Дайте определение графа.

   2. Что такое матрица смежности и матрица инцидентности?

   3. Что называется длиной пути в графе?

   4. Какой граф называется деревом?

   5. Что такое ориентированный граф?

   6. Что представляет собой сетевая модель?

   7. Дайте определение критического пути.

5. Математические модели в финансовых операциях

В настоящей главе следует обратить внимание на следующие моменты:

• существование простых и сложных процентных ставок и причины, по которым используются эти ставки;

• на влияние инфляции на исход финансовых операций и на то как учитывается это влияние в расчетах;

• как происходит погашение кредитов в отсутствие и в условиях инфляции и какова при этом разница в итоговом результате.

Участники любой финансовой операции заранее оговаривают её условия. К таким условиям относятся: сумма кредита, займа или инвестиций, цена товара, сроки и способы начисления процентов, погашения долга, сроки и порядок инвестирования финансовых средств и соответственно сроки и порядок погашения инвестиций и т. д.

Влияние на исход финансовой операции совместно многих факторов делает ее результат неочевидным. Необходимо провести детальные расчеты, чтобы оценить количественно исход финансовой операции. Знакомство с математическими моделями, позволяющими проделать такой анализ, и составляет предмет этой главы.

5.1. Простые проценты. Сложные проценты

Денежные суммы обязательно привязывают к некоторым конкретным моментам или интервалам времени. Для этого в контрактах фиксируются соответствующие сроки, даты, периодичность поступления денежных средств, их выплат.

Время играет в финансовых операциях никак не меньшую роль, чем сами размеры денежных сумм. Необходимость учитывать фактор времени диктуется принципом неравноценности денег, относящихся к различным моментам времени, так как даже при отсутствии инфляции и риска одна тысяча рублей, полученная через год, не равноценна этой же сумме, поступившей сегодня. Неравноценность объясняется тем, что теоретически любая сумма денег может быть инвестирована в коммерческое предприятие и, соответственно, принести доход. Поступившие доходы могут в свою очередь быть реинвестированы и вновь принести доход и т. д. Поэтому сегодняшние деньги несут в себе большую ценность, чем будущие, а будущие поступления мене ценны, чем сегодняшние.

Учет фактора времени при проведении финансовых операций осуществляется с помощью методов наращения и дисконтирования, в основу которых положена техника процентных вычислений.

Процентная ставка. Под процентными деньгами или процентами в финансовых расчетах понимают абсолютную величину дохода, получаемого от предоставления денег в долг в любой форме: в виде выдачи денежной ссуды, продажи в кредит, помещения денег на сберегательный счет, учета векселя, покупки сберегательного сертификата или облигаций и т. д.

Интервал времени, к которому относится процентная ставка, называется периодом начисления. Ставка измеряется в процентах либо представляется в виде десятичной или натуральной дроби.

Проценты начисляются, как правило, дискретно, т. е. в отдельные моменты времени. В качестве периодов начисления принимают год, полугодие, квартал, месяц. Иногда практикуют ежедневное начисление, а в ряде случаев удобно применять непрерывные проценты.

Проценты или выплачиваются кредитору по мере их начисления, или присоединяются к сумме долга. Процесс увеличения суммы денег в связи с присоединением процентов к сумме долга называется наращением.

В количественном финансовом анализе процентная ставка применяется не только как инструмент наращивания суммы долга, но и в более широком смысле – как измеритель степени доходности финансовой операции.

Существуют различные способы начисления процентов, зависящие от условий контракта. Разумеется, используют и различные виды процентных ставок, одно из основных различий между которыми связано с выбором исходной суммы для начисления процентов. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды или к сумме с начисленными в предыдущем периоде процентами. В первом случае они называются простыми, во втором – сложными процентными ставками.

Процентные ставки, указываемые в контрактах, могут быть постоянными или переменными («плавающими»). Во втором случае значение ставки равно сумме некоторой изменяющейся во времени базовой величины и надбавки к ней, которую называют маржой. Размер маржи определяется рядом условий, например сроком операции. Обычно маржа находится в пределах 0,5−5%.

Формула наращения по простым процентам. Под наращенной суммой ссуды (долга, депозита и т. д.) понимается ее первоначальная сумма вместе с начисленными на нее процентами к концу срока.

Пусть x₀ – первоначальная сумма денег, p – ставка простых процентов (в процентах). Начисленные проценты за один период равны x₀ · p / 100, а за k периодов − x₀ · k · p / 100.

Процесс изменения суммы долга с начисленными простыми процентами можно представить в виде арифметической прогрессии, членами которой являются величины:

x₀, x₀ + x₀ · p / 100 = x₀(1 + p / 100), x₀(1 + p / 100) + x₀ · p / 100 = x₀(1 + 2p / 100),…, x₀(1 + k p / 100).

Первый член этой прогрессии равен x₀, разность − x₀ · p / 100 , тогда последний член является наращенной суммой:

x_k = x₀ (1+ k p / 100) = x₀ (1+ k i), (5.1)

где i = p / 100, т. е. процентная ставка, выраженная десятичной дробью.

Формула (5.1) называется формулой наращения по простым процентам или формулой простых процентов, а множитель

1 + k p / 100 = 1+ k i

в этой формуле – множителем наращения. Он показывает, во сколько раз наращенная сумма больше первоначальной суммы.

Начисление простых процентов. Начисление простых процентов обычно используется в двух случаях: при заключении краткосрочных контрактов (предоставлении краткосрочных кредитов и т. п.), срок действия которых не превышает одного года, и когда проценты не присоединяются к сумме долга и выплачиваются периодически.

Ставка процентов обычно устанавливается на год. На практике же продолжительность краткосрочной операции обычно меньше года. В этом случае срок проведения операции корректируется следующим образом: величину k выражают в виде дроби

k = t / K, (5.2)

где k – срок ссуды в долях года; K – число дней и году (временная база); t - срок ссуды в днях.

В таком случае наращенная сумма вычисляется по формуле

x_k = x₀ (1+ t∙p / K∙100) = x₀ (1+ i∙t / K ). (5.3)

На практике пременяются несколько вариантов расчета процентов, различающихся временной базой K и способом измерения срока пользования ссудой.

В процессе анализа в качестве временной базы К часто удобно использовать условный или финансовый год, состоящий из 360 дней (12 месяцев по 30 дней в каждом). Исчисляемые по такой базе проценты называют обыкновенными, или коммерческими процентами. Точные проценты получают, когда за базу берут действительное число дней в году: 365 или 366 (если год високосный).

Число дней пользования ссудой также может быть точным или приближенным.

В первом случае вычисляется фактическое количество дней между двумя датами, во втором – продолжительность ссуды определяют по количеству месяцев и дней ссуды, считая все месяцы равными и содержащими по 30 дней. В обоих случаях дата выдачи и дата погашения ссуды считаются за один день.

Простые переменные ставки. Процентные ставки не всегда остаются неизменными во времени, иногда в кредитных соглашениях предусматриваются дискретно изменяющиеся процентные ставки. В этом случае формула расчета наращенной суммы приобретает следующий вид:

x_k = x₀ (1+ k₁ ∙ i₁ + k₂ ∙ i₂ +…+ k_n ∙ i_n) = x₀ (1+ 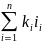). (5.4)

где x₀ – первоначальная сумма (ссуда), n – количество периодов начислений, i_i = p_i / 100 – ставка простых процентов в периоде с номером i, i=1,2,… n, k_i – продолжительность периода начисления процентов по ставке i_i.

Дисконтирование и учет. На практике часто приходится решать задачу обратную наращению процентов, когда по данной сумме x_k , соответствующей моменту окончания финансовой операции, требуется найти исходную сумму x₀. Расчет x₀ по x_k называют дисконтированием суммы x_k . В зависимости от вида процентной ставки, при анализе краткосрочных финансовых операций применяют два метода дисконтирования – математическое и коммерческое (т. н. банковский учет). В первом случае в качестве нормы приведения используют ставку i, применяемую при наращении. Во втором случае в роли нормы приведения выступает т. н. учетная ставка, для обозначения которой в дальнейшем будет использоваться символ d.

Величина x₀, найденная по x_k, называется современной величиной или текущей стоимостью суммы x_k.

Проценты в виде разности D = x_k 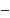x₀ называются дисконтом или скидкой. Дисконт как скидка с конечной суммы долга может определяться через процентную ставку или в виде абсолютной величины.

Процесс начисления и удержания процентов вперед называют учетом. На практике используют два принципа расчета процентов: путем наращения суммы ссуды и устанавливая скидку с конечной суммы долга. Чаще всего фактор времени учитывается в финансовых контрактах именно с помощью дисконтирования. Величина x₀ эквивалентна сумме x_k в том смысле, что через определенный период времени и при заданной ставке процентов эта величина в результате наращения станет равной x_k. Поэтому операцию дисконтирования называют также приведением. Однако понятие приведения несколько шире, чем дисконтирование. Приведение – это определение любой стоимостной величины на некоторый момент времени. Если некоторая сумма приводится к более ранней дате, чем текущая, то применяется дисконтирование, а если – к более поздней дате, то наращение. Схематически наращение и дисконтирование можно представить следующим образом:

НАСТОЯЩЕЕ		БУДУЩЕЕ
Исходная сумма Ставка		Наращенная сумма
Приведенная сумма		Возвращаемая сумма Ставка

Математическое дисконтирование. Этот вид дисконтирования представляет собой решение задачи, обратной наращению первоначальной ссуды. Если в прямой задаче

x_k = x₀ (1+ k i),

то в обратной задаче −

x₀ = x_k / (1+ k i). (5.5)

Выражение 1 / (1+ k i) в формуле (5.5) называют дисконтным множителем. Он показывает, какую долю составляет первоначальная сума ссуды в окончательной величине долга. Дисконт D суммы x_k равен

D = x_k − x₀ ,

при этом используемую норму приведения i называют декурсивной ставкой процентов.

Банковский (коммерческий учет). Операция учета, в том числе учета векселей, заключается в том, что банк до наступления срока платежа по векселю или иному платежному обязательству покупает его у владельца (являющегося кредитором) по цене ниже той суммы, которая должна быть выплачена по этому обязательству в конце срока, т. е. приобретает (учитывает) его с дисконтом.

Для расчета процентов при учете векселей применяется учетная ставка, которую обычно обозначают буквой d.

Простая годовая учетная ставка находится по формуле

d = (x_k x₀) / k x_k . (5.6)

Размер дисконта (учета), удерживаемого банком:

D = x_k – x₀ = d k x_k, (5.7)

Поэтому

x₀ = x_k − D = x_k − d k x_k = x_k (1 − d k ). (5.8)

Множитель 1 − d k называется дисконтным множителем. Срок k представляет собой период времени от момента учета векселя до даты его погашения в годах. При дисконтировании по учетной ставке чаще всего используют временную базу 360/360 или 365/360. Используемую при этом норму приведения d называют антисипативной ставкой процентов.

Учетную ставку можно использовать для наращения, т. е. для расчета x_k по x₀. Из формулы (5.12) следует, что

x_k = x₀ / (1 − d k). (5.9)

Совмещение начисления процентов по ставке наращения и дисконтирования по учетной ставке. В том случае, когда учету подлежит долговое обязательство, предусматривающее начисление простых процентов на первоначальную сумму долга, необходимо решать две задачи:

1. определить конечную сумму долга на момент его погашения;

2. рассчитать сумму, получаемую при учете, путем дисконтирования конечной суммы долга, применяя учетную ставку, действующую на момент учета.

Решение двух этих задач можно записать в виде одной формулы, содержащей наращение по ставке простых процентов, фигурирующей в долговом обязательстве, и дисконтирование по учетной ставке:

x₂ = x₁ (1+ k₁ i) (1 − k₂ d) (5.10)

где x₁ − первоначальная сумма ссуды; x₂ − сумма, получаемая при учете обязательства; k₁ − общий срок платежного обязательства, в течение которого начисляются проценты; k₂ − срок от момента учета до момента погашения долга. Эту ситуацию можно проиллюстрировать следующей схемой. Стрелки на схеме символизируют отсчет времени.

Исходная сумма x1	Период k1	Наращенная сумма xk1 = x1 (1+ k1 i)
	Период k2	Сумма при учете x2 = xk1 (1 − k2 d)

На момент погашения сумма долга через период времени k₁ составляла бы величину x_k1. Сумма, получаемая при учете, x₂ получается умножением суммы x_k1 на дисконтный множитель (1 − k₂ d), соответствующий периоду времени k₂, меньшему естественно, чем k₁.

Сложные проценты. В отличие от простых процентов, применяемых при краткосрочных финансовых операциях (до одного года), сложные проценты применяются в долгосрочных финансово-кредитных операциях, если проценты не выплачиваются периодически сразу после их начисления за прошедший интервал времени, а присоединяются к сумме долга. Присоединение начисленных процентов к сумме, которая служила базой для их определения, иногда называют капитализацией процентов.

Формула наращения по сложным процентам. Проценты на капитал можно рассматривать как награду, которую получает кредитор от заемщика за пользование капиталом, при­надлежащим кредитору.

Предположим, что заемщик кладет в банк, выплачивающий p % годовых (процентную ставку), некоторую сумму денег, которую мы для определенности, как и раньше, обозначим через x₀.

Это означает, что ровно через год у заемщика на счету будет сум­ма, равная

x₁ = x₀ + x₀ · p / 100 = x₀ (1+ i ),

а еще через год —

x₂ = x₁ + x₁ · i = x₁ (1+ i) = x₀ (1+ i) ².

Терпеливый заемщик через k лет станет обладателем суммы, рав­ной

x_k = x₀ (1+ p / 100) ^k = x₀ (1+ i) ^k . (5.11)

Здесь x_k − наращенная сумма, i − годовая ставка сложных процентов, k − срок ссуды, (1+ i) ^k − множитель (коэффициент) наращения, который обозначим К_нар..

На практике в большинстве случаев применяют дискретные проценты, т. е. проценты, начисляемые за одинаковые интервалы времени (год, полугодие, квартал и т. д.).

Наращение по сложным процентам представляет собой рост по закону геометрической прогрессии, первый член которой равен x₀ , а знаменатель –

1 + i.

Отметим, что при сроке операции менее года наращение по простым процентам дает больший результат, чем по сложным процентам, а при сроке более года – наоборот. Этим и объясняется тот факт, что при сроке финансово-кредитной операции менее года обычно применяются простые процентные ставки, а при сроке более года – сложные процентные ставки.

Графически изменения коэффициента наращения по простым и по сложным процентам представлены на рис. 5.1.

k

К_нар.

x₀

1

Рис. 5.1

Если ставка сложных процентов меняется во времени, то формула наращения принимает вид:

x_k = x₀ (1+ i₁) ^k₁ (1+ i₂) ^k₂... (1+ i_n) ^k_n , (5.12)

где i₁, i₂,… i_n − последовательные значения ставок процентов, действующих в периоды k₁, k₂,… k_n соответственно.

В этом случае выражение (1+ i₁) ^k₁ (1+ i₂) ^k₂... (1+ i_n) ^k_n является множителем наращения К_нар..

Формулы удвоения суммы. Для оценки результатов сделки кредитору и заемщику необходимо знать, через сколько лет сумма ссуды возрастет в N раз при заданной процентной ставке. Чтобы выяснить этот вопрос приравняем множитель наращения к величине N, в результате получим:

а) для простых процентов 1 + k i_прост. = N, тогда

k = (N −1) / i_прост. ; (5.13)

б) для сложных процентов (1 + i _сложн.) ^k = N, тогда

k = lnN / ln(1 + i _сложн.) (5.14)

При N = 2 формулы (5.26) и (5.27) называют формулами удвоения. Они принимают соответственно вид:

а) для простых процентов:

k = 1 / i_прост. ; (5.15)

б) для сложных процентов:

k = ln 2 / ln (1 + i _сложн.) = 0,693/ ln (1 + i _сложн.). (5.16)

Вычисления с логарифмами довольно трудоемки, поэтому для быстрой оценки величины k в (5.16) на практике иногда пользуются приближенным расчетом, известным как «правило 72». Правило заключается в следующем: если i − процентная ставка, выраженная в процентах, то 72/ i представляет собой число периодов, за которое приблизительно исходная сумма удвоится. Это правило дает неплохие результаты для небольших значений i. Следует отметить, что в большинстве финансовых расчетов процентная ставка берется в десятичных дробях, а при расчете по «правилу 72» используется i, выраженная в процентах.

Начисление процентов при дробном числе лет. При дробном числе лет проценты начисляются разными способами:

1. по формуле сложных процентов:

x_k = x₀ (1+ i) ^k ;

2. на основе смешанного метода, согласно которому на целое число лет начисляются сложные проценты, а на дробное – простые;

x_k = x₀ (1+ i) ^a (1 + bi), (5.17)

где k = a + b; a − целое число лет, b − дробная часть года;

3. в ряде коммерческих банков применяется правило, в соответствии с которым за отрезки времени меньше периода начисления проценты не начисляются, т. е.

x_k = x₀ (1+ i) (5.18)

Номинальная ставка процентов. Пусть годовая ставка сложных процентов равна j, а число периодов начисления в году равно m, тогда каждый раз проценты начисляются по ставке j / m. Ставка j называется номинальной. Начисление процентов по номинальной ставке производится по формуле

x_k = x₀ (1+ j / m ) ^N, (5.19)

где N = mk – общее число периодов начисления.

Эффективная ставка. Эффективная ставка показывает, какая годовая ставка сложных процентов дает тот же финансовый результат, что и m – разовое наращение в год по ставке j / m. Если проценты начисляются по сложной ставке m раз в год, каждый раз по ставке j / m, то можно записать равенство для множителей наращения:

(1 + i_э) ^k = (1+ j / m ) ^mk, (5.20)

где i_э – эффективная ставка, а j – номинальная. Из (5.20) нетрудно получить выражение для i_э:

i_э = (1+ j / m ) ^m – 1. (5.21)

Выражение для j имеет вид:

j = m ((1 + i_э) ^1/m – 1). (5.22)

Заметим, что эффективная ставка не зависит от величины кредита, а зависит только от номинальной ставки j и количества начислений в году m.

Понимание роли эффективной процентной ставки весьма важно для анализа финансовой деятельности предприятия. В рекламных проспектах обычно не говорится о природе процентной ставки, хотя в большинстве случаев речь идет о номинальной процентной ставке, которая может существенно отличаться от эффективной.

Учет по сложной ставке процентов. Как и в случае с простыми процентами рассмотрим два вида учета: математический и банковский.

Математический учет. В этом случае решается задача, обратная наращению по сложным процентам. Запишем исходную формулу для наращения по сложным процентам

x_k = x₀ (1+ i) ^k

и из нее определим x₀:

x₀ = x_k / (1+ i) ^k = x_k υ ^k , (5.23)

где

υ ^k = 1 / (1+ i) ^k (5.24)

− учетный или дисконтный множитель.

Если проценты начисляются m раз в году, то

x₀ = x_k / (1+ j / m ) ^mk = x_k υ ^mk, (5.25)

где

υ^mk = 1 / (1+ j / m) ^mk (5.26)

− дисконтный множитель.

Величину x₀, полученную дисконтированием x_k, называют современной (текущей) стоимостью, или приведенной величиной x_k .

Суммы x₀ и x_k эквивалентны в том смысле, что платеж в сумме x_k через k лет равноценен сумме x₀, выплачиваемой в настоящий момент. Разность D = x_k − x₀ называют дисконтом.

Банковский учет. В этом случае предполагается использование сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле

x₀ = x_k (1 − d_сл.)^k, (5.27)

где d_сл. – сложная учетная ставка.

Дисконт в этом случае определяется по формуле

D = x_k − x₀ = x_k − x_k (1 − d_сл.)^k = x_k (1 − (1 − d_сл.)^k). (5.28)

При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, так как учетная ставка каждый раз применяется к сумме, уменьшенной за предыдущий период на величину дисконта.

Номинальная и эффективная учетные ставки. В тех случаях, когда дисконтирование применяется m раз в году, используют номинальную учетную ставку f. Тогда в каждом периоде, равном 1 / m части года, дисконтирование осуществляется по сложной учетной ставке f / m. Процесс дисконтирования по этой сложной учетной ставке описывается формулой

x₀ = x_k (1− f / m ) ^N, (5.29)

где N – общее число периодов дисконтирования (N = mk).

Дисконтирование не один, а m раз в году быстрее снижает величину дисконта.

Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную (по финансовым результатам) номинальной, применяемой при заданном числе дисконтирований в году m раз.

В соответствии с определением эффективной учетной ставки найдем ее связь с номинальной учетной ставкой из равенства дисконтных множителей:

(1− f / m ) ^mk = (1 − d_сл.)^k,

откуда следует:

d_сл.= 1 − (1− f / m ) ^m (5.30)

Из выражения (5.30) следует, что эффективная учетная ставка всегда меньше номинальной.

Наращение по сложной учетной ставке. Наращение является обратной задачей для учетных ставок. Формулы наращения по сложным учетным ставкам можно получить из формул дисконтирования (5.27) и (5.29):

x_k = x₀ / (1 − d_сл.) ^k ; (5.31)

x_k = x₀ / (1− f / m ) ^N . (5.32)

Непрерывные проценты. Как было показано ранее, наращенная сумма при начислении дискретных процентов определяется по формуле

x_k = x₀ (1+ j / m ) ^mk ,

где j – общее номинальная ставка сложных процентов, m – число периодов начисления процентов в году.

Чем больше будет число периодов начисления в году m, тем меньше будут промежутки времени между моментами начисления процентов. При предельном переходе, устремив m → 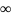, будем иметь:

x_k = 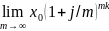= x₀ .

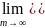Из теории пределов курса высшей математики известен второй замечательный предел: 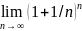. Если положить n = m / j, то нетрудно прийти к следующему равенству:

= = ,

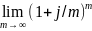где e – основание натурального логарифма.

Сопоставляя полученное выражение с предыдущей формулой нетрудно получить:

x_k = x₀ 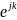. (5.33)

Чтобы отличать ставку дискретных процентов от ставки непрерывных процентов, ставку непрерывных процентов называют силой роста и обозначают буквой δ:

x_k = x₀ 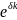. (5.34)

Как видно из вывода формулы (5.46), сила роста представляет собой номинальную ставку процентов при m → . Дисконтирование на основе непрерывных процентных ставок осуществляется по формуле:

x₀ = x_k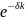 . (5.35)