6.2 Обратно-симметричные и согласованные матрицы. Индекс согласованности

Рассмотрим теперь квадратную положительную матрицу порядка n

		a11	…	a1k	…	a1n
		…	…	…	…	…
A=		ai1		aik	…	ain
		…	…	…	…	…
		an1	…	ank	…	ann

Матрица А называется обратно-симметричной, если для любых i и k выполняется соотношение

a _ki = 1 / a _ik.

Из этого, в частности, следует, что

a _ii = 1.

Матрица А называется согласованной, если для любых i, k и l выполнено равенство

a _ik a _kl = a_il.

Сравнивая свойства идеальной матрицы сравнения с приведенными определениями, приходим к выводу, что идеальная матрица сравнений — обратно-симметричная и согласованная.

Справедливо следующее утверждение.

Теорема. Положительная обратно-симметричная матрица является согласованной тогда и только тогда, когда порядок матрицы и ее наибольшее собственное значение совпадают: λ _max = n.

Индекс согласованности. Если элементы положительной обратно-симметричной согласованной матрицы А изменить незначительно («пошевелить»), то максимальное собственное значение λ_mах также изменится незначительно. Пусть А − произвольная положительная обратно-симметричная матрица и λ_mах − ее наибольшее собственное значение.

Если

λ_mах = n,

то матрица А — согласованная.

Если

λ_mах 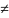n

(всегда λ_mах n), то в качестве степени отклонения положительной обратно-симметричной матрицы А от согласованной можно взять отношение

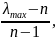
которое называется индексом согласованности (ИС) матрицы А и является показателем близости этой матрицы к согласованной.

Замечание. Считается, что если ИС не превышает 0,10, то можно быть удовлетворенным степенью согласованности суждений.

6.3 Вычисление собственных характеристик обратно-симметричной матрицы

Довольно естественно встает вопрос о том, как находить наибольшее собственное значение λ_mах положительной обратно-симметричной матрицы.

1-й способ:

1. суммируем элементы каждой строки и записываем полученные результаты в столбец;

2. складываем все элементы найденного столбца;

3. делим каждый из элементов этого столбца на полученную сумму.

2-й способ:

1. суммируем элементы каждого столбца и записываем получен­ные результаты в столбец;

2. заменяем каждый элемент построенного столбца на обратный ему;

3. складываем элементы столбца из обратных величин;

4. делим каждый из этих элементов на полученную сумму.

3-й способ:

1. суммируем элементы каждого столбца;

2. делим элементы каждого столбца на их сумму;

3. складываем элементы каждой строки полученной матрицы;

4. записываем результаты в столбец;

5. делим каждый из элементов последнего столбца на порядок исходной матрицы п.

4-й способ:

1. перемножаем элементы каждой строки и записываем получен­ные результаты в столбец;

2. извлекаем корень n-й степени из каждого элемента найденного столбца;

3. складываем элементы этого столбца;

4. делим каждый из этих элементов на полученную сумму.

5-й способ:

1)возводим матрицу парных сравнений в достаточно высокую степень;

2)суммируем элементы каждой строки и записываем полученные результаты в столбец;

3)складываем элементы этого столбца;

4)делим каждый из этих элементов на полученную сумму.

Следует пояснить, что такое достаточно высокая степень. С увеличением степени будет расти точность вычисления собственного вектора матрицы. Как только точность вычислений будет удовлетворять наперед заданной величине, степень можно считать достаточной.

Каждый из этих способов, будучи примененным к иде­альной матрице, приводит к одному и тому же точному результату.