Регрессия
В практических исследованиях возникает необходимость аппроксимировать (описать приблизительно) диаграмму рассеяния математическим уравнением.
Для линейной зависимости это сделать просто: корреляционный эллипс можно заменить прямой линией. В прямоугольной системе координат уравнение прямой линии записывается в виде:
Это математическое выражение корреляционной зависимости называется уравнением регрессии. Коэффициенты а и b называются параметрами уравнения регрессии, а определяет отрезок, отсекаемый прямой линией на оси Y, b—изменение Y при изменении X на единицу и называется также коэффициентом регрессии.
Уравнение регрессии тем лучше описывает зависимость, чем меньше рассеяние диаграммы, чем больше теснота взаимосвязи. Уравнение прямой линии пригодно для описания только линейных зависимостей. В случае нелинейных зависимостей математическая запись может отображаться уравнениями параболы, гиперболы и др.
Все коэффициенты корреляции и регрессии дают лишь количественную меру связи, но ничего не говорят о причинах зависимости. Определить эти причины — дело самого исследователя.
Вычисление парного линейного коэффициента корреляции Бравэ-Пирсона
Вычисление значения коэффициента взаимосвязи — механическая процедура счета. Однако ей должны предшествовать некоторые вопросы, на которые необходимо ответить. Эти вопросы относятся к изучаемым показателям и формулируются следующим образом: в какой шкале измеряется изучаемый показатель? Как много измерений этого показателя выполнено? Можно ли считать ряд измерений показателя выборкой, имеющей нормальный закон распределения? и др. Каждый случай связан с вычислением определенного коэффициента взаимосвязи.
Парный линейный коэффициент корреляции Бравэ-Пирсона используется только в случае, если результаты измерены по шкале интервалов или отношений и форма взаимосвязи линейная!
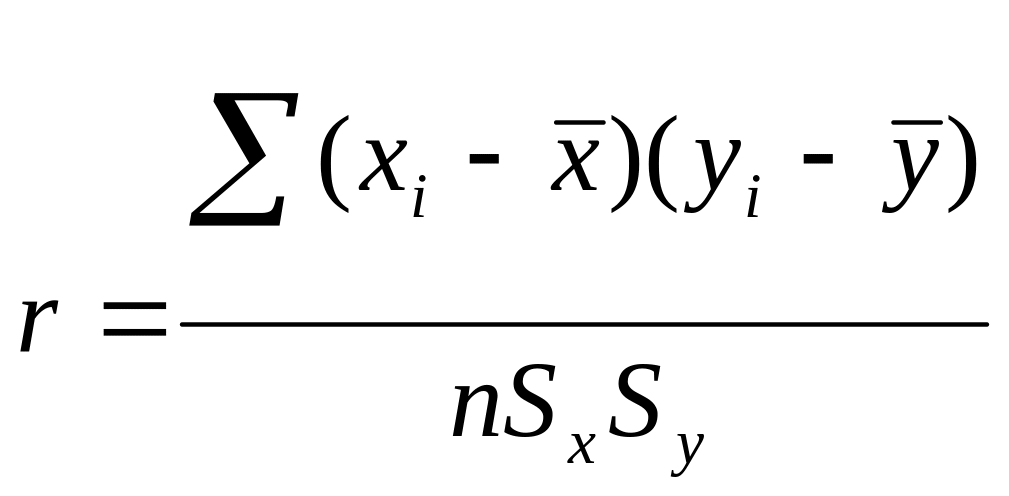
В некоторых случаях тесноту взаимосвязи определяют на основании коэффициента детерминации, который вычисляют по формуле:
Этот коэффициент определяет часть общей вариации одного показателя, которая объясняется вариацией другого.
Вычисление коэффициентов уравнения регрессии
В случае линейной зависимости уравнение регрессии является уравнением прямой линии. И таких уравнений два: прямое и обратное.
Значение коэффициентов регрессии вычисляется по формулам
Коэффициент регрессии b имеет размерность равную отношению размерностей изучаемых показателей X и Y, и тот же знак, что и коэффициент корреляции.
Для оценки качества уравнения регрессии вычисляется остаточное среднее квадратическое отклонение.
Эти оценки абсолютны и поэтому не могут быть сравнимы друг с другом, поэтому вводят оценки относительной погрешности уравнений, выраженные в процентах.
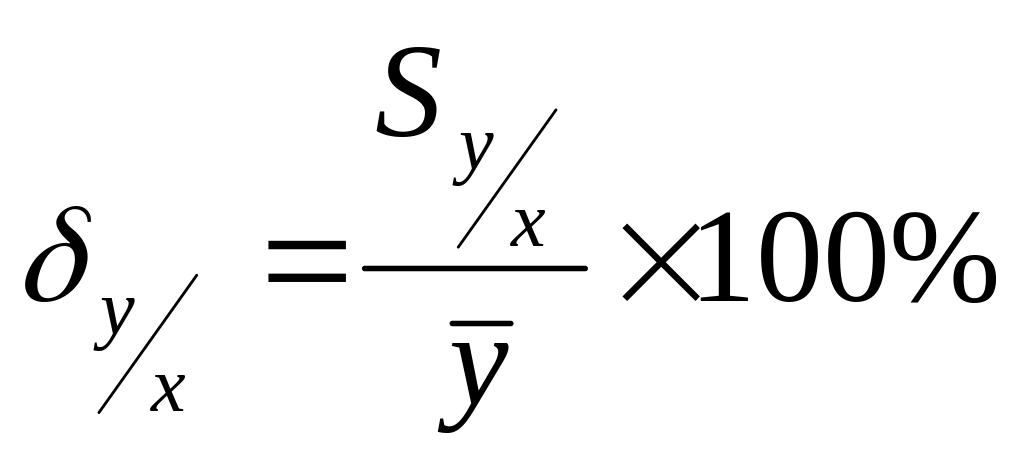
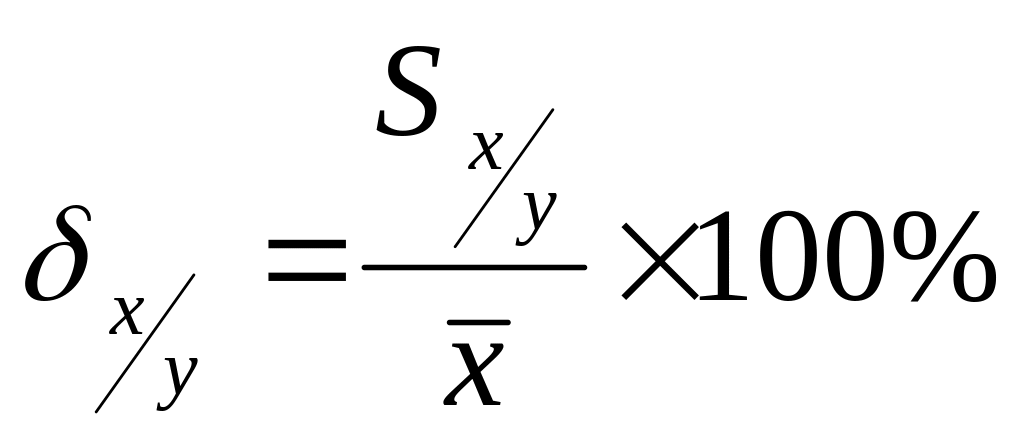
Погрешность которого уравнения будет меньшей, то и будет являться более точным, а, следовательно, и приемлемым на практике.
Пример практических расчетов
расчет рангового и тетрахорического коэффициентов корреляции
Расчет рангового и тетрахорического коэффициентов корреляции Расчет рангового коэффициента корреляции Спирмэна
Если полученные в ходе исследования значение измерены по шкале порядка, то для оценки взаимосвязи пользуются ранговыми коэффициентами корреляции.
Наиболее часто используется ранговый коэффициент корреляции Спирмена, который рассчитывается по формуле:
Пример. Можно ли утверждать, что мнения двух судей, оценивавших на соревнованиях по фигурному катанию выступления мужчин в обязательной программе, были согласованными, если они поставили 9 участниками следующие оценки:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Иванов ( ) |
4,7 |
4,9 |
5,1 |
5,6 |
5,7 |
5,3 |
5,8 |
5,9 |
5,5 |
Петров ( |
4,3 |
4,5 |
5,3 |
5,2 |
5,5 |
5,5 |
5,9 |
5,6 |
5,7 |
)
Проранжируем результаты и попарно и присвоим им соответствующие номера. Результаты занесем в таблицу. Если два или более результата имеют равные значения, их ранг рассчитывается как среднее арифметическое занимаемых ими рангов.
№ |
|
|
|
|
|
|
|
|
4,7 |
4,3 |
1 |
1 |
0 |
0 |
|
|
4,9 |
4,5 |
2 |
2 |
0 |
0 |
|
|
5,1 |
5,3 |
3 |
4 |
-1 |
1 |
|
|
5,6 |
5,2 |
6 |
3 |
3 |
9 |
|
|
5,7 |
5,5 |
7 |
5,5 |
1,5 |
2,25 |
|
|
5,3 |
5,5 |
4 |
5,5 |
-1,5 |
2,25 |
|
|
5,8 |
5,9 |
8 |
9 |
-1 |
1 |
|
|
5,9 |
5,6 |
9 |
7 |
2 |
4 |
|
|
5,5 |
5,7 |
5 |
8 |
-3 |
9 |
|
|
|
|
|
0 |
28,5 |
Подставим полученные данные в формулу.
Сделаем вывод. Так как полученное нами расчетное значение коэффициента корреляции относится к диапазону 0,99-0,7, то между мнениями двух судей существует сильная положительная статистическая взаимосвязь, то есть их можно считать согласованными.