КУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра геометрии
В.А. Долженков., Е.Г. Соловьева, И.В. Горчинский
МЕТОД КООРДИНАТ
Курск – 2009 г.
Печатается по решению редакционно-
издательского совета университета
Метод координат: Учеб.-метод. пособие / сост. В.А. Долженков,
Е.Г. Соловьева, И. В.Горчинский − Курск: Курск. гос. ун-т, 2009. – 53 с.
Данное учебно-методическое пособие предназначено для студентов 1-го курса по специальности 010100 Математика по курсу «Аналитическая геометрия» (количество часов 200).
Пособие содержит теоретический и практический материал по теме, примеры выполнения контрольных заданий.
Рецензент: Фрундин В.Н., канд. педагогических наук
ã Долженков В.А., Соловьёва Е.Г., Горчинский И.В., сост. 2009
ã Курский государственный университет, 2009
Оглавление
§ 1. Аффинные системы координат ……………….4
§ 2. Прямая на плоскости …………… 9
§ 3. Уравнения плоскости в пространстве ……………….. 21
§ 4. Уравнения прямой в пространстве ………………30
§ 5. Полярная система координат ………………43
Решение нулевого варианта контрольной работы …………… 46
Тест …………….51
Список литературы ……………… 53
§ 1. Аффинные системы координат
В
дальнейшем будем обозначать: Е3
– трехмерное
точечное пространство, V3
– трехмерное
векторное пространство. Выберем
произвольную точку О
Е3
и произвольный (аффинный) базис {
}
пространства V3.
Определение
1. Набор,
состоящий
из
точки О
и базиса {
}
называется аффинной системой координат
в пространстве Е3.
Обозначаем: О
.
Точку
О называют началом координат, а векторы
– координатными векторами. Прямую О
,
заданную точкой О и вектором
называем осью Ох,
прямую О
– осью Оу,
а прямую О
–
осью Оz.
Одновременно с осями координат мы
выделяем координатные плоскости, которые
делят все пространство на 8 частей.
Плоскость определяемая осями Ох
и Оу
обозначаем Оху
и, аналогично, плоскости Охz,
Оуz.
С помощью аффинной системы координат, мы будем сопоставлять каждой точке набор чисел – ее координаты.
Рассмотрим
произвольную точку М
Е3.
Одновременно с точкой М
мы получим
вектор
,
который имеет координаты (х;
у; z)
в базисе {
}:
(х;
у; z).
Эту тройку чисел (х;
у; z)
мы называем аффинными координатами
точки М
в О
:
М (х; у; z).
Если
в качестве базиса выбрать ортонормированную
тройку векторов {
},
то получим прямоугольную декартовую
систему координат О
.
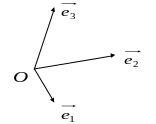
Для
построения точки М(х;
у; z)
по ее координатам в О
поступаем следующим образом: от точки
О
откладываем вектор
= х
,
от точки М1
откладываем вектор
= y
,
далее откладываем от точки М2
вектор
= z
.
По правилу многоугольника получим
= + + = х + y + z .
М заданная точка.
Ломаная ОМ1М2М называется координатной ломаной точки М. В дальнейшем часто систему координат О будем обозначать Охуz.
Итак,
мы определили координаты точки, зная
понятие координаты вектора. С другой
стороны, пусть мы имеем в Охуz
две точки
А(х1;
у1;
z1)
и В(х2;
у2;
z2).
Одновременно мы получим векторы
,
(х2;
у2;
z2)
и
(х1;
у1;
z1).
Из векторного равенства
=
−
находим координаты вектора
(х2
– х1;
у2
– у1;
z2
– z1).
Простое отношение трех точек
Пусть в аффинной системе координат Охуz заданы различные точки А(х1; у1; z1), В(х2; у2; z2) и точка М(х; у; z), лежащая на прямой (АВ).
Определение 2. Назовем простым отношением трех точек А, В и М число , если имеет место равенство:
.
(1)
Обозначаем: = (АВ, М).
Следует
обратить внимание, что
М
В, так как
и равенство
нельзя получить ни при каком .
С другой стороны, значения
могут быть как положительные (
),
так и отрицательные (
),
и возможно
= 0 (М = А).
Решим задачу о нахождении координат точки М, если известно простое отношение , в котором она делит направленный отрезок АВ.
Пусть М(х; у; z), тогда
(
х –
х1;
у – у1;
z
– z1),
(х2
– х; у2
– у; z2
– z).
Равенство (1) в координатной форме имеет вид:
х – х1 = (х2 – х),
у – у1 = (у2 – у),
z – z1 = (z2 – z).
Отсюда находим:
,
,
.
(2)
Частный случай, когда М является серединой отрезка АВ, дает координаты точки М:
,
,
.
(3)