§ 5. Полярная система координат
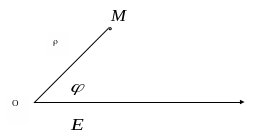
Для определения положения точки на плоскости можно пользоваться и другими системами координат. В частности широко используется полярная система координат. На плоскости выберем точку и обозначим ее О. Рассмотрим луч с началом в О, а на луче выберем единичный отрезок ОЕ. Точка О называется полюсом, а луч ОЕ называется полярной осью. Положение любой точки М на плоскости, отличной от О определяется парой чисел: расстоянием = |OM| и величиной угла между лучами ОЕ и ОМ, причем угол ориентирован, т. е. положительное направление против часовой стрелки, а отрицательное – по часовой стрелке. Для точки О считаем = 0, а угол не определен.
Для рассматриваемых полярных координат мы имеем 0, а R. Однако, в нашем случае пары чисел (, ) и (, + 2 к), где к – любое целое число, представляют собой координаты одной и той же точки плоскости. Поэтому выделяют главные значения угла 0 < 2.
Рассмотрим одновременно с полярной системой координат прямоугольно декартовую, у которой начало координат совпадает с О, а ось абсцисс содержит полярную ось, причем сохраняет положительное направление оси и масштаб. В этом случае обе эти системы координат однозначно определяют друг друга.
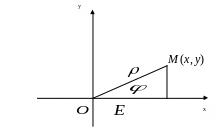
С одной стороны:
а с другой :
,
,
.
В полярной системе координат уравнение окружности с центром в полюсе О и радиусом R имеет вид: = R.
Уравнение луча ОА, составляющего угол с полярной осью, имеет вид: = .
Обобщенные полярные координаты
В
полярной системе координат О
всегда выполняется неравенство 
.
Поэтому не всякая пара действительных
чисел является полярными координатами
точки. Например, пара (–1;
). Для устранения этого недостатка
вводят так называемые обобщенные
полярные координаты точки. Пусть (;
)
– произвольная пара действительных
чисел. Если
0, то этой парой числе задается точка с
полярными координатами (;
).
Если
0, то будем считать, что этой парой чисел
(;
)
определяется точка А,
симметричная точке Ã(||;)
относительно полюса О.
Можно говорить не о симметричности относительно полюса О, а прибавлять к углу число .
Например,
пара чисел (−3;
)
задает точку А
с полярными координатами (3;
).
Пример 1. Найдем уравнение прямой, не проходящей через полюс О. Зададим эту прямую числом р, длиной отрезка ОР и углом , где Р – основание перпендикуляра ОР на прямую, а –ориентированный угол между лучом ОР и полярной осью.
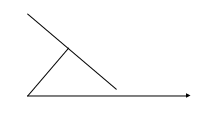
Если произвольная точка М(, ) принадлежит данной прямой, то р = cos ( −) и обратно.
Поэтому
имеем уравнение прямой:
.
Пример
2. Луч
вращается вокруг своего начала О
с постоянной скоростью w.
Найти параметрические уравнения
траектории точки М,
если она начала движение от точки А
¹О,
и движется по лучу со скоростью
пропорциональной расстоянию |OM|.
Решение. Примем за полярную систему координат начальное положение луча , где точка О будет полюсом. За параметр t примем время. Тогда положение точки М через промежуток t определяется значениями полярных координат r и j, где r изменяется от значения до + ¥. При этом r¢ = lr , а j = wt. Из дифференциального уравнения
r¢ = lr
находим:
Þ
Þln
-
ln
=
lt
Þ
.
Рассмотрим согласованную с полярной системой координат прямоугольную декартовую систему. Известна связь между координатами этих систем.
.
Заменяя полярные координаты, получим параметрические уравнения траектории точки М:
