
- •§ 1. Аффинные системы координат
- •Простое отношение трех точек
- •Задание фигур в пространстве
- •§ 2. Прямая на плоскости Различные виды уравнений прямой на плоскости
- •Угол между прямыми на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Расстояние от точки до прямой
- •§ 3. Уравнения плоскости в пространстве
- •Угол между плоскостями
- •Расстояние от точки до плоскости
- •§ 4. Уравнения прямой в пространстве
- •Взаимное расположение двух прямых в пространстве
- •Общее уравнение прямой в пространстве
- •Расстояние от точки до прямой в пространстве
- •Расстояние между двумя прямыми в пространстве
- •Взаимное расположение прямой и плоскости
- •Угол между прямой и плоскостью
- •§ 5. Полярная система координат
- •Обобщенные полярные координаты
- •Решение нулевого варианта контрольной работы
- •Список литературы
- •305000, Г. Курск, ул. Радищева, 33
Решение нулевого варианта контрольной работы
Найти уравнение плоскости, проходящей через прямую
![]()
перпендикулярно плоскости: 3х – 5 у + 5 z + 3 = 0.
Решение.
Искомая плоскость
будет проходить через данную прямую, а
следовательно через точку прямой М0
(2; – 3; – 1).
Направляющий вектор
![]() заданной прямой и нормальный вектор
заданной прямой и нормальный вектор
![]() заданной плоскости параллельны искомой
плоскости. Так как векторы
заданной плоскости параллельны искомой
плоскости. Так как векторы
![]() и
не коллинеарные (их координаты не
пропорциональны), то составим уравнение
плоскости в виде определителя по точке
и двум неколлинеарным векторам:
и
не коллинеарные (их координаты не
пропорциональны), то составим уравнение
плоскости в виде определителя по точке
и двум неколлинеарным векторам:
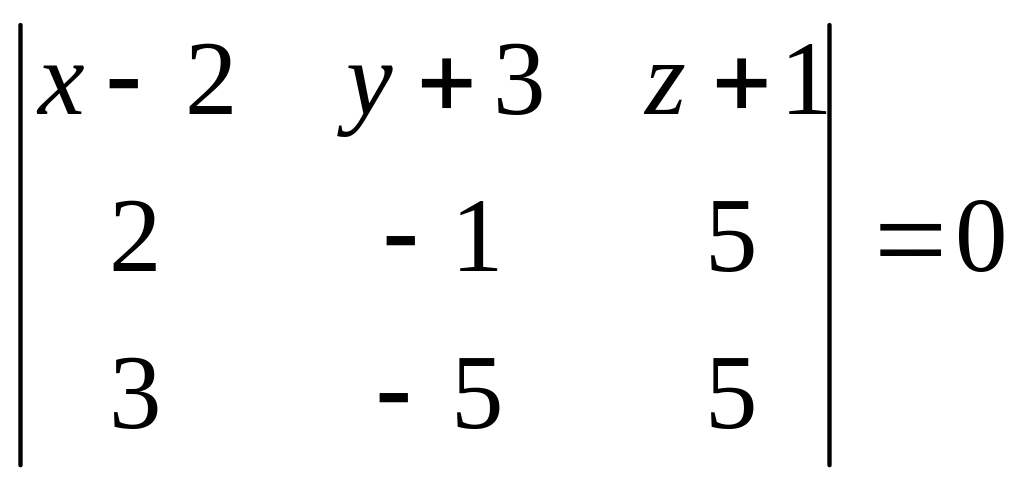 .
.
Разложим определитель по первой строке
![]() .
.
![]() ,
,
:
![]() .
.
Ответ: .
Даны плоскости, заданные в О уравнениями:
: 2х – 3у + 3 = 0, : х – у + z +2 = 0.
Найти уравнение плоскости, проходящей через линию пересечения данных плоскостей и перпендикулярную плоскости .
Решение. Найдем две общие точки данных плоскостей. Для этого решим систему уравнений:
![]()
Пусть у = 0, тогда система примет вид
![]()
Отсюда
получим, что х
=
![]() ,
z =
,
z =
![]() .
.
Решением
системы будет тройка чисел
![]() .
Искомая точка М1
.
Пусть у
= 1, тогда система примет вид
.
Искомая точка М1
.
Пусть у
= 1, тогда система примет вид
![]()
Отсюда
получим, что х
= 0, z =
![]() .
Решением системы
будет тройка чисел
.
Решением системы
будет тройка чисел
![]() .
Искомая точка М2
.
.
Искомая точка М2
.
Из
уравнения плоскости
находим ее нормальный вектор
![]() .
.
Для
составления уравнения искомой плоскости
обратим внимание на то, что точки
М1
и М2
принадлежат
ей, а вектор
будет ей параллелен. Поэтому составляем
уравнение плоскости по точке М2
и двум неколлинеарным векторам
![]()
![]() и
.
Можно заменить вектор
и
.
Можно заменить вектор
![]() на вектор
на вектор
![]() .
Запишем уравнение в виде определителя:
.
Запишем уравнение в виде определителя:
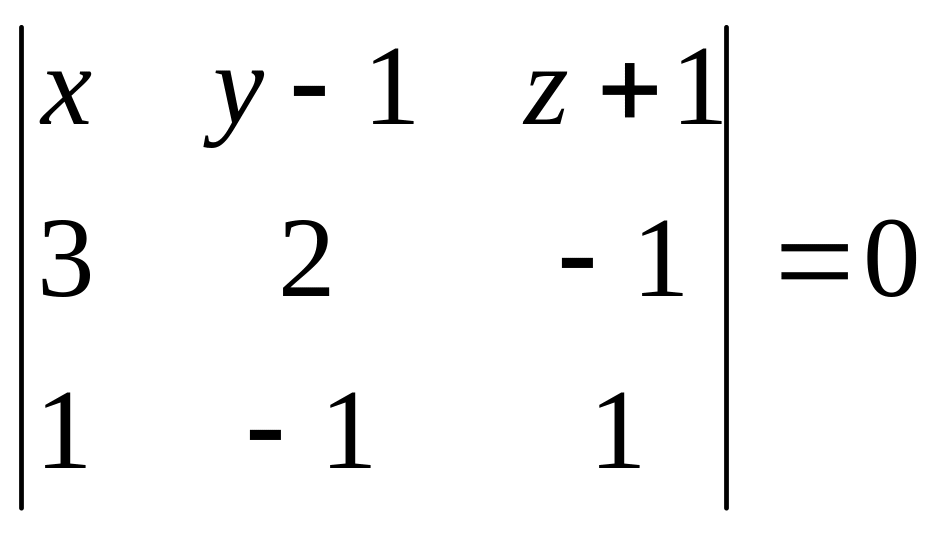 .
.
Разложив определитель по первой строке, получим уравнение искомой плоскости:
![]() .
.
Найти каноническое уравнение прямой, проходящей через точку А(6; 2; 3) перпендикулярно плоскости, проходящей через точки В (1; 4; 4), С (0; 2; 4), D (1; 3; 3).
Решение. Найдем уравнение плоскости (BCD) по трем точкам B, C, D
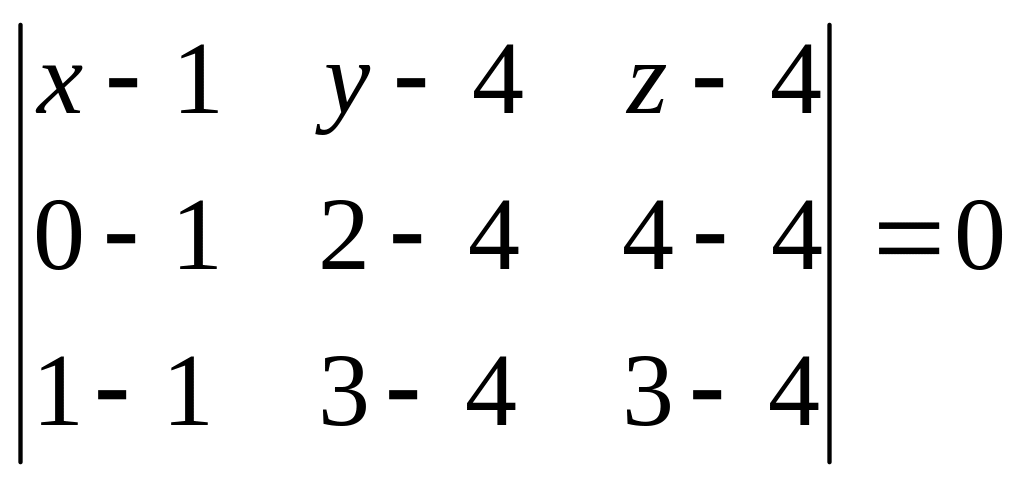 ,
,
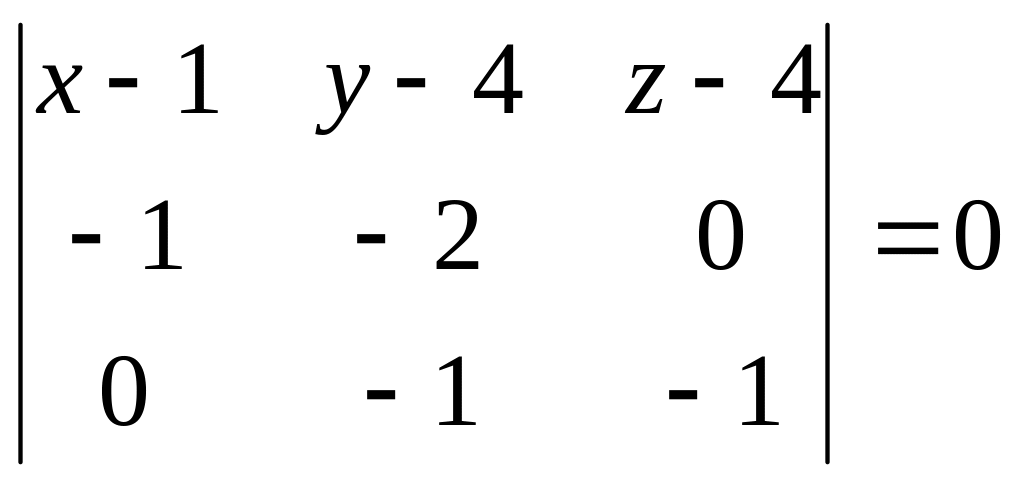 .
.
Разложив определитель по первой строке, получим уравнение плоскости (BCD):
![]() .
.
Нормальный
вектор
![]() плоскости (BCD)
будет направляющим вектором искомой
прямой. Составим канонические уравнения
прямой по точке А(6;
2; 3)
и направляющему вектору
:
плоскости (BCD)
будет направляющим вектором искомой
прямой. Составим канонические уравнения
прямой по точке А(6;
2; 3)
и направляющему вектору
:
![]() .
.
Ответ: .
4. Даны прямые, заданные в О уравнениями:
ℓ1:
![]() и
ℓ2:
и
ℓ2:
![]() .
.
Найти уравнение плоскости, проходящей через первую прямую параллельно второй прямой.
Решение.
Согласно условию задачи точка М0
(– 1; – 1; 4),
принадлежащая первой прямой, лежит в
искомой плоскости. Кроме этого имеем
два вектора:
![]() ,
направляющий вектор прямой ℓ1
и
,
направляющий вектор прямой ℓ1
и
![]() ,
направляющий вектор прямой ℓ2,
которые параллельны искомой плоскости
и не параллельны между собой. Составим
уравнение плоскости
,
направляющий вектор прямой ℓ2,
которые параллельны искомой плоскости
и не параллельны между собой. Составим
уравнение плоскости
:
 .
.
Раскрываем определитель по первой строке:
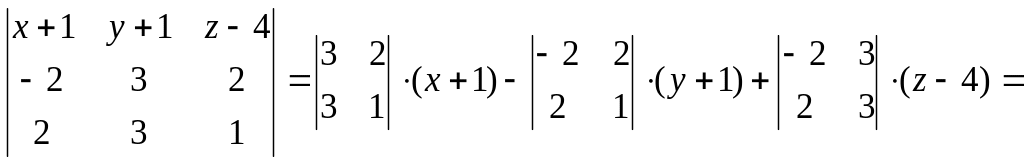
= – 3(х + 1) + 6(у +1) – 12(z – 4) = – 3х + 6у – 12z +51.
Следовательно,
– 3х + 6у – 12z +51 = 0
и получаем уравнение плоскости
: х –2у + 4z – 17 = 0.
5. Вычислить расстояние от точки P (-1; 1; -2) до плоскости, проходящей через точки, заданные в О : А (1; 4; 4), B (0; 2; 4), C (1; 3; 3).
Решение. Найдем уравнение плоскости (АВС) по трем заданным точкам:
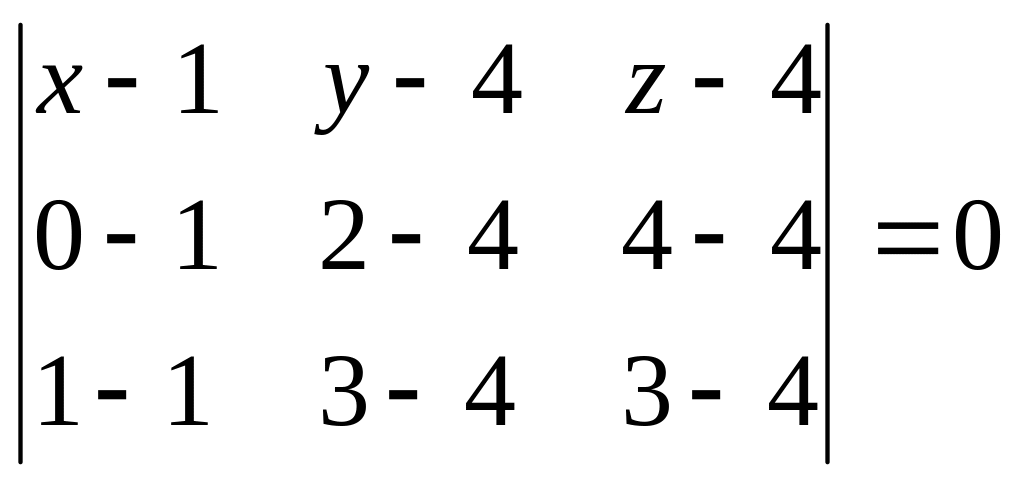 .
.
Разложив определитель по первой строке, получим:
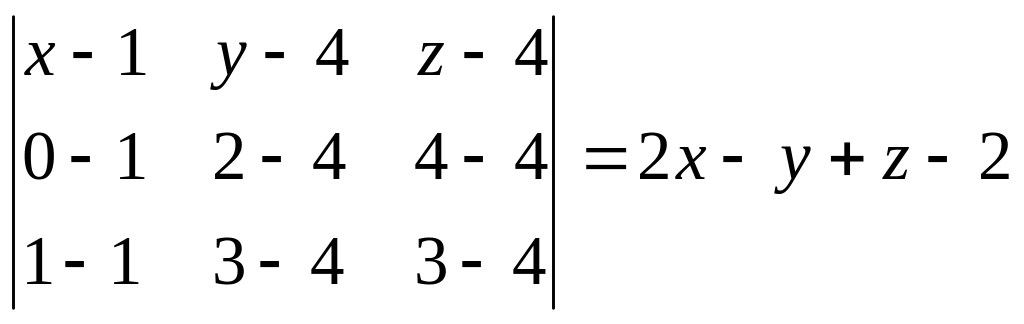 .
.
Следовательно,
![]() = 0 уравнение плоскости (АВС).
= 0 уравнение плоскости (АВС).
Воспользуемся известной формулой для вычисления расстояния от точки до плоскости
![]() .
.
Ответ:
![]() .
.
Тест
Отметьте номер правильного ответа в бланке ответов
|
Задания |
Варианты ответов |
А1 |
Написать уравнение прямой, проходящей через две заданные точки М1(1; – 2; 1) и М2(3; 1; – 1) |
1) 3) 5)
|
A2 |
Найти
расстояние от точки М0 (–1; 2) до
прямой ℓ:
|
1) |
A3 |
Найти
расстояние между прямыми ℓ1:
|
1)
|
А4 |
Найти косинус угла между прямыми ℓ1 и ℓ2, если ℓ1 : и ℓ2:
|
1)
|
А5 |
Найти
уравнение касательной к окружности
|
1)
3) 5)
|
А6 |
Две стороны квадрата лежат на прямых ℓ1
: |
1) 64 2) 81 3) 16 4) 49 5) 25 |
А7
|
В
О
|
1)
3)
у = х +1 4)
5) х – у + 1=0 |
А8 |
В О заданы точки: А(1; 0), В(0; 1), С(1; 2) Найти общее уравнение медианы (АМ) треугольника АВС.
|
1) 5)
|
А9 |
В О заданы точки: А(1; 1), В(0; 2), С(2; 4) Найти общее уравнение биссектрисы угла АВС.
|
1) х – у = 0, 2) 2х+3у – 1 =0, 3) х = 2, 4) у – 2 = 0, 5) у = 2х. |
А10 |
В О заданы точки: А(1; 1),В(0; 2), С(2; 4). Вычислить расстояние от точки А до биссектрисы угла В в треугольнике АВС.
|
1) 1, 2) -2, 3) 4, 4) 0, 5) 2. |
А11 |
В О заданы точки:А(1; 1), В(0; 2), С(2; 4). Вычислить площадь треугольника АВВ1 , где ВВ1 - биссектриса угла В в треугольнике АВС.
|
1)
2, 2)
|
А12 |
В
О |
1)х – у - 8z=19; 2)21x - 3y - 24z+19=0; 3)x - 3y+5z - 21=0; 4) x+3y - 5z - 21=0; 5) 21x - 3y+24z+19=0 |
A13 |
Уравнение прямой имеет вид, если она проходит через точку В(4,2,-3) и перпендикулярна плоскости ACD, где A(1,-1,1), C(0,2,4), D(1,3,3), (O ). |
1)21x-3y+24z+19=0;2) 3)
5)
|
А14 |
Уравнение плоскости ACD имеет вид, где A(1,-1,1),C(0,2,4), D(1,3,3), (O ). |
1) 3х – у + 2z – 6 =0, 2) 3х + у + 2z + 6 =0, 3) у + 2z – 6 =0, 4) 3х + 2z – 6 =0, 5) 3х – у -2z – 6 =0 |
A15 |
Найти расстояние от точки B(4,2,-3) до плоскости ACD, где A(1,-1,1),C(0,2,4), D(1,3,3), (O ). |
1)
2, 2)
|
Ответы
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
А8 |
А9 |
А10 |
А11 |
А12 |
А13 |
А14 |
А15 |
2 |
5 |
3 |
1 |
1 |
4 |
5 |
4 |
4 |
5 |
3 |
2 |
3 |
1 |
2 |
