
- •§ 1. Аффинные системы координат
- •Простое отношение трех точек
- •Задание фигур в пространстве
- •§ 2. Прямая на плоскости Различные виды уравнений прямой на плоскости
- •Угол между прямыми на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Расстояние от точки до прямой
- •§ 3. Уравнения плоскости в пространстве
- •Угол между плоскостями
- •Расстояние от точки до плоскости
- •§ 4. Уравнения прямой в пространстве
- •Взаимное расположение двух прямых в пространстве
- •Общее уравнение прямой в пространстве
- •Расстояние от точки до прямой в пространстве
- •Расстояние между двумя прямыми в пространстве
- •Взаимное расположение прямой и плоскости
- •Угол между прямой и плоскостью
- •§ 5. Полярная система координат
- •Обобщенные полярные координаты
- •Решение нулевого варианта контрольной работы
- •Список литературы
- •305000, Г. Курск, ул. Радищева, 33
§ 3. Уравнения плоскости в пространстве
Плоскость
в пространстве однозначно задается
точкой и двумя неколлинеарными векторами.
Пусть в О
плоскость p
задана точкой М0(х0;
у0
; z0)
и неколлинеарными векторами
![]() и
и
![]() .
Если М(х; у;
z)–
произвольная точка, то очевидно
утверждение
.
Если М(х; у;
z)–
произвольная точка, то очевидно
утверждение
М
Î
p
Û
(![]() .
(1)
.
(1)
Если записать смешанное произведение в координатной форме, то получим уравнение плоскости
 =
0. (2)
=
0. (2)
Уравнение
(1) можно записать в векторном виде,
учитывая, что векторы
и
![]() неколлинеарные:
неколлинеарные:
![]() .
(3)
.
(3)
Уравнение (3) можно записать в координатной форме
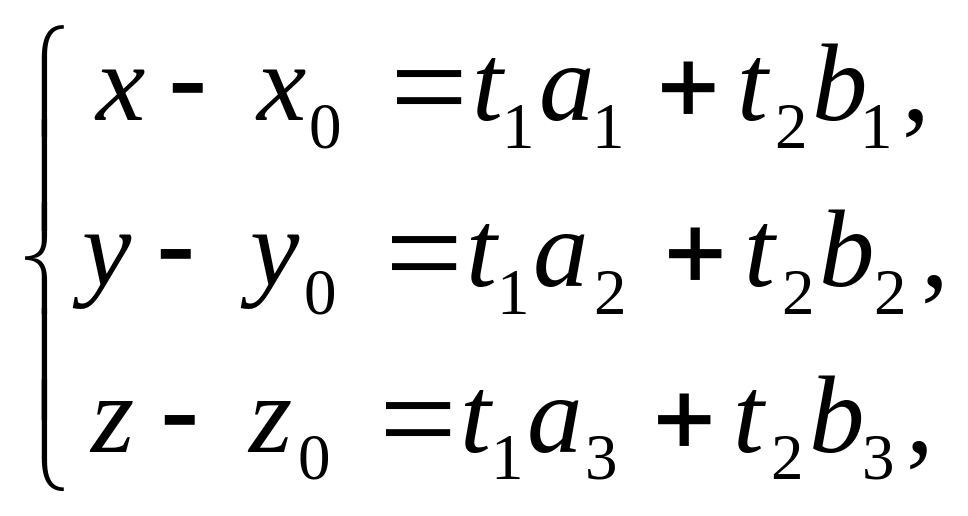 или
или
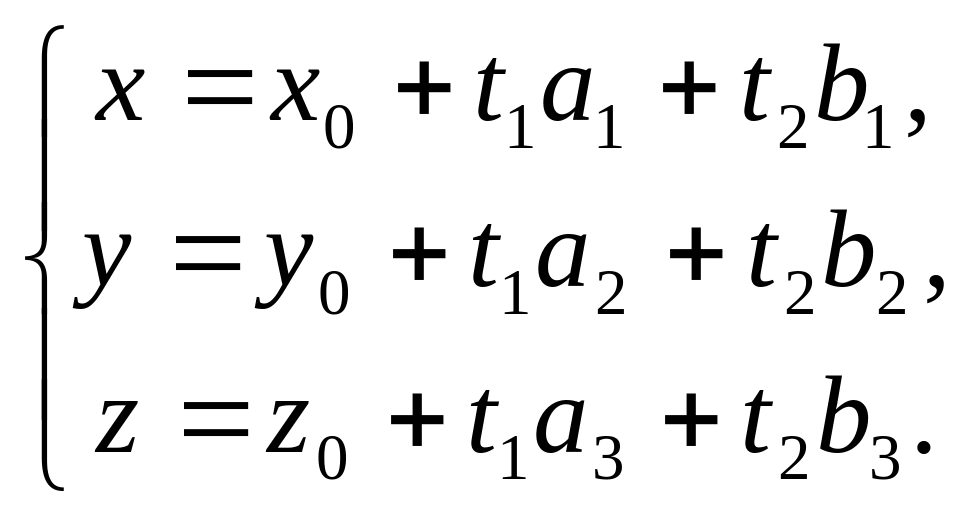 (4)
(4)
Уравнения (4) называют параметрическими уравнениями плоскости.
Если определитель в уравнении (2) разложить по первой строке, то получим:
![]() =
0.
=
0.
Обратим внимание, что определители второго порядка одновременно не могут равняться нулю, так как векторы и неколлинеарные.
Раскроем скобки и, введя новые обозначения, получим уравнение вида
![]() =
0,
=
0,
![]() .
(5)
.
(5)
Таким образом, всякая плоскость имеет уравнение вида (5). Покажем, что и любое уравнение вида (5) задает некоторую плоскость. Действительно, если, например, В ¹ 0, то левую часть уравнения (5) можно записать в виде определителя
=
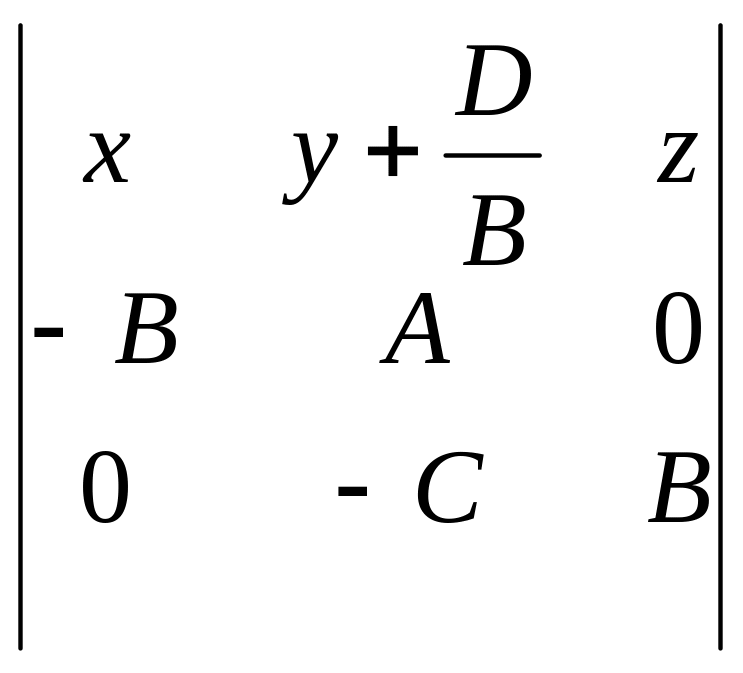 ,
,
т.е. уравнение (5) примет известный нам вид (2):
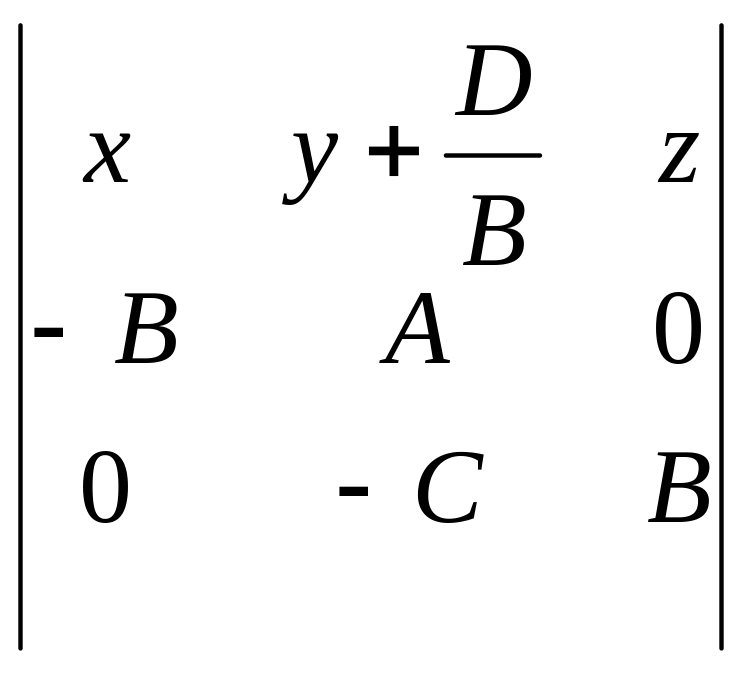 =
0.
=
0.
Следовательно,
уравнение (5) является уравнением
плоскости, заданной точкой М0(0;
–![]() ;
0) и парой не
коллинеарных векторов
(–
В, А, 0) и
(0,
– С, В). Итак,
уравнение (5) является уравнением
плоскости, которое называют общим
уравнением.
;
0) и парой не
коллинеарных векторов
(–
В, А, 0) и
(0,
– С, В). Итак,
уравнение (5) является уравнением
плоскости, которое называют общим
уравнением.
Замечание.
Если предположить, что А ¹
0, то уравнение (5) определяет плоскость,
заданную точкой М0(–
![]() ;
0; 0) и парой
неколлинеарных векторов
(–
В, А, 0)
и
(–
С, 0, А).
Случай С ¹
0 рассмотреть
самостоятельно.
;
0; 0) и парой
неколлинеарных векторов
(–
В, А, 0)
и
(–
С, 0, А).
Случай С ¹
0 рассмотреть
самостоятельно.
Уравнение плоскости, заданной точкой и нормальным вектором
Определение 1. Ненулевой вектор, перпендикулярный плоскости, называют нормальным вектором данной плоскости.
Пусть
плоскость
![]() задана
в О
некоторой точкой М0(х0,;
у0;
z0)
и нормальным вектором
задана
в О
некоторой точкой М0(х0,;
у0;
z0)
и нормальным вектором
![]() .
Если М(х; у;
z)
– произвольная точка, то очевидно
утверждение
.
Если М(х; у;
z)
– произвольная точка, то очевидно
утверждение
М
Î
p
Û
![]() .
(6)
.
(6)
Если записать условие перпендикулярности в виде скалярного произведения, причем в координатной форме, то получим искомое уравнение плоскости
![]() =
0,
.
(7)
=
0,
.
(7)
Сравнивая уравнения (5) и (7), замечаем, что коэффициенты уравнения (5) в О являются координатами нормального вектора плоскости.
Уравнение плоскости, заданной тремя точками, не лежащими на одной прямой вывести самостоятельно.
Можно
воспользоваться известным уравнением
(2). Пусть в О![]() плоскость p
задана точками
М1(х1,
у1,
z1),
М2(х2,
у2,
z2),
М3(х3,
у3,
z3),
не лежащими на одной прямой и М(х,
у, z)-
произвольная точка плоскости. Тогда
уравнение плоскости p
имеет вид
плоскость p
задана точками
М1(х1,
у1,
z1),
М2(х2,
у2,
z2),
М3(х3,
у3,
z3),
не лежащими на одной прямой и М(х,
у, z)-
произвольная точка плоскости. Тогда
уравнение плоскости p
имеет вид
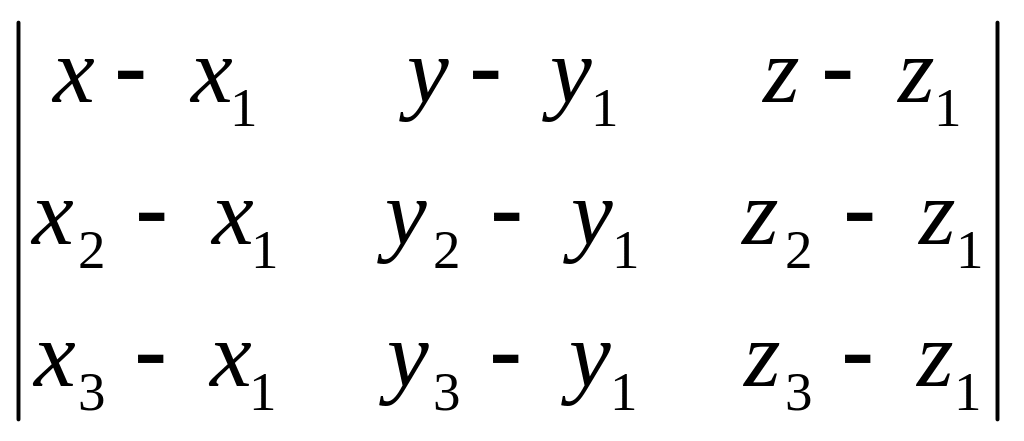 =
0. (8)
=
0. (8)
Угол между плоскостями
Пусть плоскости p и p1 заданы в О общими уравнениями
=
0 и
![]() =
0.
=
0.
Тогда
имеем их нормальные векторы, соответственно,
и
![]() .
.
Две пересекающиеся плоскости образуют две пары вертикальных двугранных углов. Если найти один из этих углов, то остальные углы находятся непосредственно. Один из двугранных углов j между плоскостями численно равен углу между нормальными векторами к этим плоскостям.
Поэтому
cosj
=
![]()
или
cosj
=
![]() .
.
Как следствие ( = 900) получим условие перпендикулярности плоскостей:
![]() =
0.
=
0.
Так как свойство параллельности плоскостей равносильно коллинеарности их нормальных векторов, то получим условие параллельности плоскостей:
1.
p
Ç
p1
¹
Æ
Ù
p
¹
p1
Û
![]() Ú
Ú
![]()
![]() Ú
Ú
![]() .
.
2.
p
¤¤
p1
Ù
p¹
p1
Û
![]() =
¹
=
¹![]() .
.
3. p= p1 Û = = .
