
- •§ 1. Аффинные системы координат
- •Простое отношение трех точек
- •Задание фигур в пространстве
- •§ 2. Прямая на плоскости Различные виды уравнений прямой на плоскости
- •Угол между прямыми на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Расстояние от точки до прямой
- •§ 3. Уравнения плоскости в пространстве
- •Угол между плоскостями
- •Расстояние от точки до плоскости
- •§ 4. Уравнения прямой в пространстве
- •Взаимное расположение двух прямых в пространстве
- •Общее уравнение прямой в пространстве
- •Расстояние от точки до прямой в пространстве
- •Расстояние между двумя прямыми в пространстве
- •Взаимное расположение прямой и плоскости
- •Угол между прямой и плоскостью
- •§ 5. Полярная система координат
- •Обобщенные полярные координаты
- •Решение нулевого варианта контрольной работы
- •Список литературы
- •305000, Г. Курск, ул. Радищева, 33
Угол между прямыми на плоскости
Определение. Углом между прямыми называется наименьший из двух смежных углов, образованных этими прямыми.
Для решения вопроса о нахождении угла между прямыми достаточно заменить прямые их направляющими векторами и находить острый угол между векторами.
Пусть прямые ℓ1 и ℓ2 заданы общими уравнениями в прямоугольной декартовой системе координат О :
ℓ1:
![]() = 0,
= 0,
ℓ2:
![]() = 0.
= 0.
Направляющие векторы этих прямых имеют координаты 1(В1, – А1) и 2(В2, – А2). Пусть угол между прямыми равен . Тогда
cos
=
![]()
или
cos
=
![]() .
(7)
.
(7)
При решении задач часто сталкиваемся с нахождением угла между прямыми, когда прямые ℓ1 и ℓ2 задаются уравнениями с угловым коэффициентом (не забываем, что прямые ℓ1 и ℓ2 не параллельны оси Оу):
ℓ1:
![]() ,
,
ℓ2:
![]() .
.
Если переписать эти уравнения в общем виде, то получим
ℓ1:
![]() = 0,
= 0,
ℓ2:
![]() = 0.
= 0.
Соответственно, их направляющие векторы 1(1, k1) и 2(1, k2), и формула (7) принимает вид:
cos
=
![]() .
.
Более интересна формула для угла между прямыми ℓ1 и ℓ2 :
![]() =
=
![]() .
.
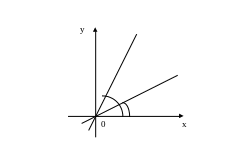
Действительно,
![]() ,
,
![]() (см. рисунок). Тогда
один из углов между прямыми ℓ1
и ℓ2
:
= |
(см. рисунок). Тогда
один из углов между прямыми ℓ1
и ℓ2
:
= |![]() |.
Так как
|.
Так как
=
|
![]() |
= |
|
= |![]() |,
|,
то
= .
Замечание.
Если ℓ1
ℓ2,
то
– не существует и
![]() = –1.
= –1.
Взаимное расположение двух прямых на плоскости
Пусть
прямые ℓ1
и ℓ2
заданы общими уравнениями в О
![]() :
:
ℓ1: = 0,
ℓ2: = 0.
Вопрос о взаимном расположении двух прямых можно решить алгебраическим путем, а именно, исследуя решение системы линейных уравнений
![]()
Как известно, система имеет единственное решение только в единственно случае, когда коэффициенты при неизвестных не пропорциональны
![]() .
Следовательно,
.
Следовательно,
1. ℓ1 ℓ2 ℓ1 ℓ2 .
2.
ℓ1||ℓ2
ℓ1
ℓ2
![]() (
(![]()
![]() ).
).
3.
ℓ1
=
ℓ2
=
![]() ( прямые совпадают).
( прямые совпадают).
Расстояние от точки до прямой
Пусть прямая ℓ задана общим уравнением в О :
ℓ: = 0.
Нормальный
вектор прямой имеет координаты:
![]() .
Выберем произвольно точку М0(
.
Выберем произвольно точку М0(![]() )
и найдем расстояние от точки М0
до прямой ℓ.
)
и найдем расстояние от точки М0
до прямой ℓ.
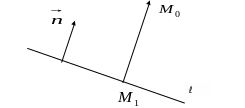
Из
точки М0
опустим
перпендикуляр на прямую ℓ
и обозначим
основание
перпендикуляра
М1(![]() ).
Так как М1
ℓ, то
).
Так как М1
ℓ, то
![]() = 0 и
= 0 и
С
= – (![]() ).
(8)
).
(8)
Искомое
расстояние равно |М1М0|.
С другой стороны
![]() ||
||
![]() и, следовательно, угол
между ними равен или 0, или .
и, следовательно, угол
между ними равен или 0, или .
Поэтому:
(
,
)
= |
|
|
|cos
=
|
|
|
|
=
|
|![]() .
.
Запишем полученное равенство в координатной форме.
Имеем:
(![]() .
.
Поэтому, учитывая (8) получим:
(
,
)
=
![]() =
=
![]() =
=
![]() .
.
Учитывая, что скалярное произведение векторов может быть отрицательным, будем рассматривать его по абсолютной величине и находим
| | = | |,
|М1М0|
=
![]() .
(9)
.
(9)
Знак трехчлена Ах + Ву + С
Пусть прямая ℓ задана общим уравнением в О :
ℓ: = 0.
Нормальный
вектор прямой имеет координаты:
.
От произвольной точки
![]() прямой
ℓ откладываем представитель
прямой
ℓ откладываем представитель
![]() вектора
.
вектора
.
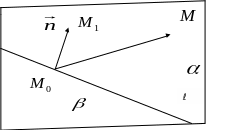
Как
известно прямая ℓ разбивает плоскость
на две открытые полуплоскости, которые
обозначим
и ,
причем полуплоскость
содержит отрезок
![]() .
.
Тогда,
как нетрудно заметить, если точка М(![]() )
расположена в полуплоскости ,
то угол между векторами
)
расположена в полуплоскости ,
то угол между векторами
![]() и
и
![]() будет острый. Если точка М
расположена в полуплоскости ,
то угол между векторами
и
будет тупой. Рассматривая скалярные
произведения этих векторов, получим:
будет острый. Если точка М
расположена в полуплоскости ,
то угол между векторами
и
будет тупой. Рассматривая скалярные
произведения этих векторов, получим:
Если точка М расположена в полуплоскости , то ( ,
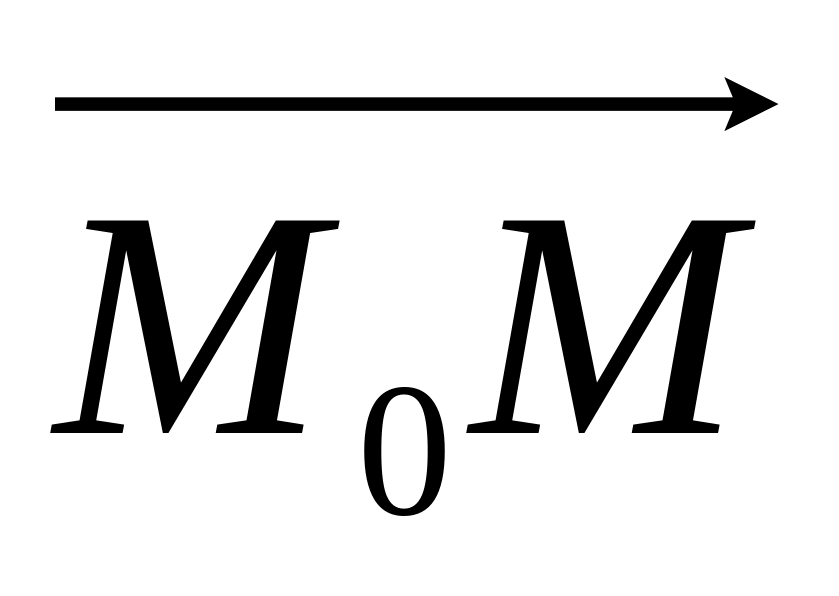 )
> 0.
)
> 0.Если точка М расположена в полуплоскости , то ( , ) < 0.
Записывая 1 и 2 в координатной форме, получим:
М
![]() >
0,
>
0,
М < 0.
Учитывая,
что точка
![]()
ℓ, (см (8)) получим:
ℓ, (см (8)) получим:
М
![]() > 0, (10)
> 0, (10)
М < 0. (11)
Таким образом, строгие неравенства (10), (11) являются уравнениями открытых полуплоскостей. Если неравенства нестрогие, т.е.
≥ 0, (12)
0. (13),
то они являются уравнениями полуплоскостей (вместе с граничной прямой ℓ).
Пример. В прямоугольной декартовой системе координат на плоскости заданы точки: А(2; −1), В(−1; 3), С(4; −5).
1) Составить уравнения прямой АВ в канонической, параметрической и общей формах. Определить координаты ее нормального вектора.
2) Определить угловой коэффициент прямой (АС) и отрезки, отсекаемые ею на осях координат.
3) Найти косинус угла между прямыми (АВ) и (АС).
4) Найти длину высоты треугольника АВС, проведенной из вершины С и составить уравнение прямой, содержащей этот отрезок.
Решение.
1. Прямую (АВ)
можно задать точкой А(2;
−1) и вектором
![]() ,
тогда каноническое и параметрическое
задания данной прямой будут выглядеть
следующим образом:
,
тогда каноническое и параметрическое
задания данной прямой будут выглядеть
следующим образом:
![]() (1)
(1)
и
![]() где
где
![]() R.
(2)
R.
(2)
Из канонического уравнения (1) равносильными переходами получим ее общее уравнение:
![]() ,
,
![]() .
(3)
.
(3)
Из
уравнения (3) найдем координаты нормального
вектора этой прямой:
![]() .
.
2. Аналогично пункту (1) можно получить общее уравнение прямой (АС): 2x + y − 3 = 0.
Откуда
y = −2x + 3.
Следовательно, угловой коэффициент этой прямой k = − 2.
Уравнение прямой (АС) запишем в виде: 2x + y = 3 и, разделив обе части уравнения на 3, получим
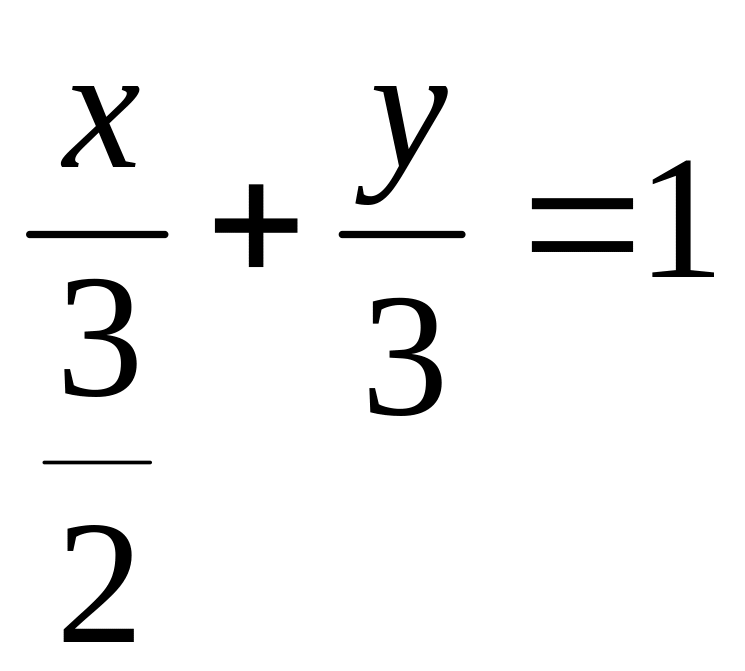 .
.
Мы
получили уравнение прямой в отрезках.
Отсюда находим точки пересечения прямой
с осями координат:
![]() ,
B(0;3)
,
B(0;3)
3. Для нахождения косинуса угла между прямыми (АВ) и (АС) используем следующую формулу:
![]() ,
,
где
![]() –угл между прямыми,
k1,
k2
– угловые коэффициенты данных прямых.
Во второй части задания мы нашли k2
= −2.
–угл между прямыми,
k1,
k2
– угловые коэффициенты данных прямых.
Во второй части задания мы нашли k2
= −2.
Общее уравнение прямой (АВ) получено в первой части задания:
4x
+ 3y
− 5 = 0, откуда
![]() и k1=
и k1=
![]() .
.
Следовательно,
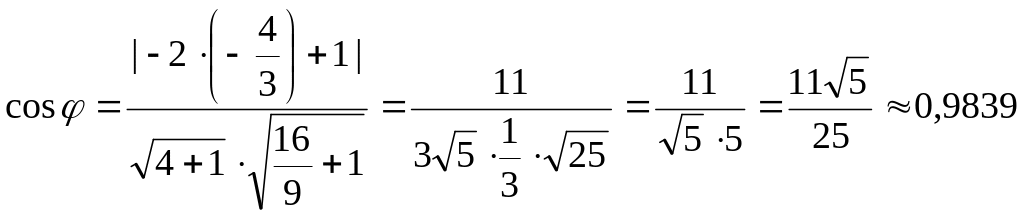 .
.
Итак,
![]() .
.
4 .
.
Длину
высоты
![]() можно рассматривать как расстояние от
точки С(4;−5).до прямой (АВ):
можно рассматривать как расстояние от
точки С(4;−5).до прямой (АВ):
![]() .
.
Т
H![]() .
Формула расстояния от точки до прямой
известна:
.
Формула расстояния от точки до прямой
известна:
![]() .
.
Следовательно,
![]() .
.
Итак, |CH|=0,8.
Прямую
(CH)
можно задать точкой С(4;
-5) и нормальным
вектором
![]() .
Поэтому −3
∙(x
− 4) + 4 ∙(y
+5)=0,
.
Поэтому −3
∙(x
− 4) + 4 ∙(y
+5)=0,
3x - 4y – 32 = 0 – уравнение прямой (CH).
