§ 4. Уравнения прямой в пространстве

Прямая ℓ в пространстве однозначно задается точкой и направляющим вектором. Пусть в О прямая ℓ задана точкой М₀(х₀, у₀, z₀) и не нулевым вектором . Если М(х, у, z)- произвольная точка, то

нетрудно заметить, что верно следующее утверждение:

МÎℓ Û ||‌‌ . (1)

Так как

|| Û = t , где t – действительное число,

то имеем уравнения прямой, которые называем параметрическими уравнениями 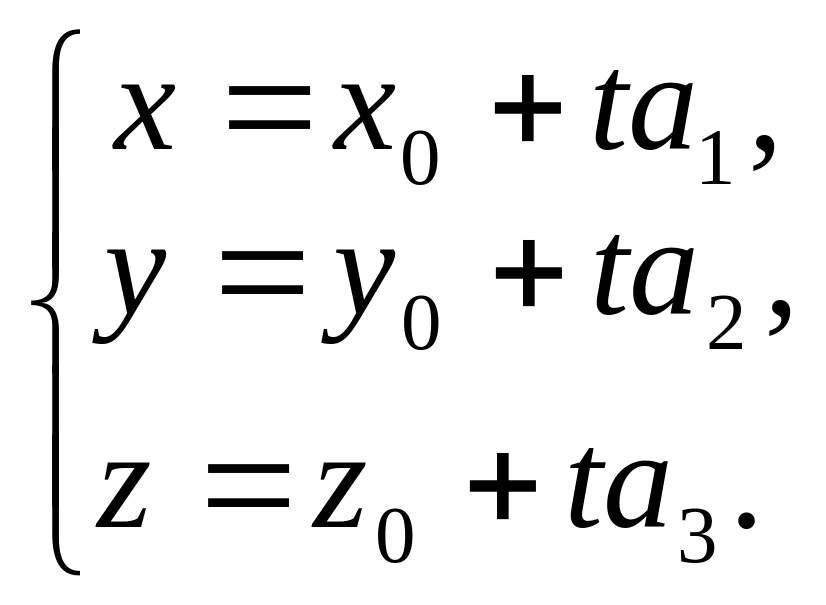(2)

Так как

|| Û ,

то имеем уравнения прямой, которые называем каноническими уравнениями.

. (3)

При записи уравнения (3) допускается запись нуля в знаменателе, так как в этом случае запись считается формальной. Эта запись подразумевает равенство числителя нулю.

Прямая ℓ в пространстве однозначно задается также двумя точками.

Пусть в О прямая ℓ задана различными точками М₁(х₁, у₁, z₁) и М₂(х₂, у₂, z₂). Одновременно рассматриваем вектор (х₂-х₁, у₂-у₁, z₂-z₁) как направляющий вектор прямой. При этом уравнение (3) примет новый вид, и мы получили уравнения прямой, заданной двумя точками:

. (4)

Взаимное расположение двух прямых в пространстве

Пусть прямые ℓ₁ и ℓ₂ заданы каноническими уравнениями:

ℓ₁: ,

ℓ₂: .

Из уравнений следует, что точки М₁(х₁, у₁, z₁) и М₂(х₂, у₂, z₂) лежат , соответственно, на прямых ℓ₁ и ℓ₂, а векторы и являются их направляющими векторами. Наша задача, пользуясь уравнениями прямых, найти условия, определяющие параллельность прямых, пересечение прямых и условия, когда эти прямые будут скрещивающимися.

Так как параллельность прямых однозначно определяется коллинеарностью их направляющих векторов, то получим :

ℓ₁ ||ℓ₂ Û || Û , (5)

в частности,

ℓ₁ = ℓ₂ Û || Ù М₂ Î ℓ₁ Û Ù . (5¢)

Прямые ℓ₁ и ℓ₂ являются скрещивающимися. Следовательно, эти прямые не лежат в одной плоскости. Тогда тройка векторов , , - не может быть параллельна одной плоскости, то есть эта тройка некомпланарная.

Условие компланарности тройки векторов § нам известно. Поэтому получаем: прямые ℓ₁ и ℓ₂ являются скрещивающимися тогда и только тогда, когда тройка векторов , , - некомпланарная, что в координатной форме выглядит так:

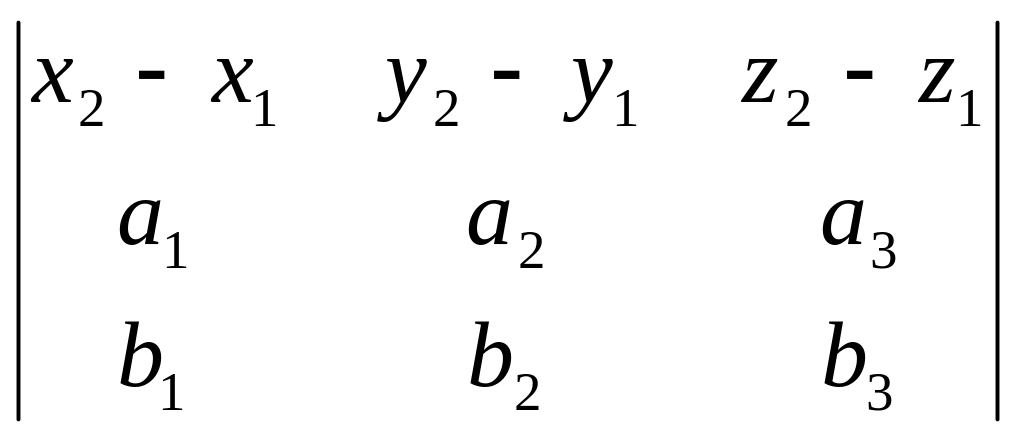¹ 0. (6)

Пусть прямые ℓ₁ и ℓ₂ пересекаются, тогда они лежат в одной плоскости и в этой плоскости не параллельны. Следовательно, условия (5), (5¢) и (6) не выполняются. Поэтому получаем условие, когда прямые ℓ₁ и ℓ₂ пересекаются:

( Ú Ú ¹ )Ù = 0.

Общее уравнение прямой в пространстве

Пусть плоскости p₂ и p₁ заданы в О общими уравнениями

= 0 и = 0.

Предположим, что плоскости пересекаются, а, значит, пересекаются по прямой ℓ. Следовательно, выполняется условие

Ú Ú . (7)

Тогда система уравнений

(8)

и является уравнением прямой ℓ, которое мы называем общим уравнением прямой.

Замечание. Зная общее уравнение прямой можно получить канонические уравнения этой прямой.

Пример. Прямая ℓ задана общим уравнением

ℓ: (1)

Написать канонические уравнения прямой.

Решение. Для решения нам достаточно найти две различные точки данной прямой. Для этого мы найдем два различных решения системы (1).

Перепишем систему (1) в виде

Пусть х =1, тогда у =2, а z= - 4. Если положить х = 0, то у =1, а z = - 1.

Таким образом, мы получили два решения системы, а, следовательно, две точки прямой: А(1, 2,−4), В(0, 1, −1).

Для составления канонических уравнений прямой выберем точку А(1, 2,−4) и вектор (1, 1, −3) за точку и направляющий вектор данной прямой.

Уравнения имеют вид :