
- •§ 1. Аффинные системы координат
- •Простое отношение трех точек
- •Задание фигур в пространстве
- •§ 2. Прямая на плоскости Различные виды уравнений прямой на плоскости
- •Угол между прямыми на плоскости
- •Взаимное расположение двух прямых на плоскости
- •Расстояние от точки до прямой
- •§ 3. Уравнения плоскости в пространстве
- •Угол между плоскостями
- •Расстояние от точки до плоскости
- •§ 4. Уравнения прямой в пространстве
- •Взаимное расположение двух прямых в пространстве
- •Общее уравнение прямой в пространстве
- •Расстояние от точки до прямой в пространстве
- •Расстояние между двумя прямыми в пространстве
- •Взаимное расположение прямой и плоскости
- •Угол между прямой и плоскостью
- •§ 5. Полярная система координат
- •Обобщенные полярные координаты
- •Решение нулевого варианта контрольной работы
- •Список литературы
- •305000, Г. Курск, ул. Радищева, 33
§ 2. Прямая на плоскости Различные виды уравнений прямой на плоскости
Составим уравнение прямой , проходящей через две различные точки М1(х1; у1) и М2 (х2; у2).
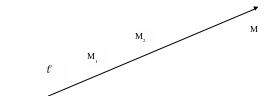
Пусть
М(х; у)
произвольная
точка прямой .
Точка М(х;
у) лежит на
прямой
тогда и только тогда, когда векторы
![]() и
и
![]() коллинеарные. Поэтому справедливо
равенство
коллинеарные. Поэтому справедливо
равенство
![]() .
.
Здесь
– некоторое число. Из векторного
равенства следует равенство одноименных
координат:
![]() и
и
![]() .
.
Из последнего равенства получим:
![]()
![]() .
.
Это уравнение называется уравнением прямой, проходящей через две заданные точки.
Любую прямую на плоскости можно однозначно задать точкой и не нулевым вектором, параллельным прямой. Этот вектор называется направляющим вектором прямой.
Пусть
в Оху прямая
ℓ
задана точкой М0
(х0;
у0)
и направляющим вектором
![]() (,
).
Пусть М(х; у)
– произвольная точка
прямой.
(,
).
Пусть М(х; у)
– произвольная точка
прямой.
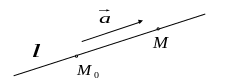
Нетрудно заметить, что верно следующее утверждение:
Мℓ
![]() ||
.
(1)
||
.
(1)
Так как
|| = t , где t – действительное число,
то получаем уравнения прямой, которые называем параметрическими уравнениями
ℓ:
![]() (2)
(2)
Так как
||
![]() ,
,
то получим уравнение прямой, которое называем каноническим уравнением
ℓ: . (3)
Замечание. В уравнении (3) допускается запись нуля в знаменателе, так как в этом случае запись считается формальной. Эта запись подразумевает равенство нулю числителя.
Уравнение (3), при условии 0, можно переписать в виде
![]() =
=
![]()
и,
обозначив отношение
![]() =
=
![]() ,
получим уравнение
с угловым коэффициентом
,
получим уравнение
с угловым коэффициентом
![]()
![]() ,
(4)
,
(4)
где
–
угловой коэффициент,
![]() .
.
Так как 0, то уравнение (4) имеют только прямые непараллельные оси Оу.
Замечание. Еще в школьном курсе, рассматривая уравнение прямой (4) в прямоугольно декартовой системе координат, было отмечено, что угловой коэффициент к = tg , где – ориентированный угол между прямой и осью абсцисс.
Уравнение
(3) можно привести к виду
![]() =
(
) . Раскрывая скобки,
получим уравнение вида
=
(
) . Раскрывая скобки,
получим уравнение вида
х – у + (у0 - х0) = 0
или
![]() =
0, (5)
=
0, (5)
где А = , В = – , А2 + В2 0, С = у0 - х0 .
Итак, мы показали, что любая прямая имеет уравнение вида (5). Покажем, что и любое уравнение вида (5), при условии А2 + В2 0 задает некоторую прямую. Действительно, при наших ограничениях уравнение (5) имеет решение. Пусть это будет пара (х0; у0). Тогда получим:
![]() =
0,
=
0,
![]() =
0.
=
0.
Из этих равенств получаем:
![]()
![]() (
(![]() ) = 0.
) = 0.
От этого уравнения легко переходим к уравнению вида (3):
![]() ,
,
которое
определяет нам прямую, заданную точкой
М0
(х0,
у0)
и направляющим вектором
(![]() ).
).
Следовательно, мы показали, что уравнение (5) является уравнением прямой, которое называют общим уравнением. При этом вектор ( ) является направляющим вектором прямой (5).
Уравнение прямой, заданной точкой и нормальным вектором
Определение. Ненулевой вектор, перпендикулярный прямой называется нормальным вектором этой прямой.
Прямую
на плоскости в О![]() можно однозначно задавать точкой и
нормальным вектором. Пусть прямая ℓ
задана точкой М0(х0,
у0)
и нормальным вектором
можно однозначно задавать точкой и
нормальным вектором. Пусть прямая ℓ
задана точкой М0(х0,
у0)
и нормальным вектором
![]() .
. 
Тогда выполняется следующее утверждение:
Мℓ
![]() .
.
Так как
![]() ,
,
то получим искомое уравнение прямой ℓ:
. (6)
Замечание.
Если раскрыть скобки в уравнении (6), то
получим общее уравнение прямой (5).
Следовательно, если прямая задана общим
уравнением (5) в О
,
то из уравнения находим нормальный
вектор к прямой:
![]() .
.
