Конспект лекций по ТАУ

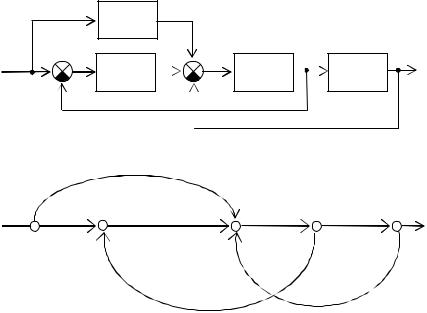
Контуры в этом примере касаются всех путей, поэтому дополнительные множители путей 1 = 2 = 1

Окончательно можно записать:

2
	∑ Pi	i			+ W2W3W5W6
W (s) =	i=1		=	W1W3W5W6		,
				1 − W3W5W4 + W5W6W7

что соответствует ранее полученному результату.

Пример 2.25. Рассмотрим структуру, показанную на рис. 2.25.

W2(s)
X(s)		Y(s)
W1(s)	W3(s)	W4(s)

W2(s)

X(s)

1

W1(s)

W3(s)

W4(s) Y(s)

– 1

– 1

Рис. 2.25. Структурная схема и сигнальный граф

От входа к выходу ведут два пути:

P1=W1W3W4, P2= W2W3W4.

101

В графе есть два контура:
L1= –W 1W3,	L2= –W 3W4.

Контур L1 касается контура L2 , поэтому определитель графа вычисляется по формуле

= 1 − (L1 + L2 ) .

Контуры здесь касаются всех путей, поэтому дополнительные множители путей 1 = 2 = 1.

Окончательно можно записать:

2
	∑ Pi	i			+ W2W3W4
W (s) =	i=1		=	W1W3W4		.
				1 + W1W3 + W3W4

Таким образом, использование сигнальных графов и применение формулы Мейсона позволяет алгоритмизировать процесс упрощения структурной схемы.

Пример 2.26. Рассмотрим систему и соответствующий ей сигнальный граф, приведенный на рис. 2.26.

От входа к выходу ведут два пути:

P1=W1W2,	P2= W3.
В графе есть два контура:
L1= –W 1,	L2= –W 2.
Определитель графа

= 1 − (L1 + L2 ) .

Дополнительные множители путей

1 = 1;

2 = 1 − L2 .

102

X(s)		=	5		=	1	Y(s)
	W1			W2
			s + 3			s + 4
	W3	=	1
			2s + 1
X(s)	1		W1(s) 1	W2(s) 1			Y(s)
			– 1	– 1
				W3(s)

Рис. 2.26. Пример многоконтурной системы Передаточная функция

2

∑ Pi

i

W (s) =

i=1

=

W1W2 + W3 (1 + W2 )

.

1 + W1 + W2

Подставляя численные значения, получаем:

2

∑ Pi

i

W (s) =

i=1

=

=

s5 + 29s4 + 258s3

+ 988s2 + 1664s + 960

.

2s6

+ 49s5

+ 460s4 + 2124s3 + 5001s2 + 5384s +

1680

103

Пример 2.27. Определить максимальное целое число µ, при котором для входного воздействия g(t) = tµ установившаяся ошибка слежения в системе, изображенной на рис. 2.27, будет равна нулю.

s T2 s + 1

X(s)	E(s)	k	Y(s)
			1
		T1s + 1	s

Рис. 2.27. Структурная схема следящей системы

Решение.

Определим ПФ замкнутой системы. Для этого построим сигнальный граф (рис. 2.28).

W1

1

1

W2

W3

1

-1

Рис. 2.28. Сигнальный граф системы

От входа к выходу ведут два пути:

P1=W1W3,

P2= W2W3.

104

В графе есть один контур

L1= –W 2W3,

Определитель графа вычисляется по формуле

= 1 − L1 .

Контур касается всех путей, поэтому дополнительные мно-

жители путей

1 = 2

= 1.

Окончательно можно записать:

2

∑ Pi

i

W1W3 + W2W3

W (s) =

i =1

=

.

1+W2W3

1

+

k

(T s2 + s + kT s + k )(T s2 + s)

W (s) =

T s + 1

T s2 + s

=

2

k

(T1s2 + s + k )(T1s2 + s)(T2s + 1) =

1

1

2

1

1 +

(T s2 + s)

1

T s2

+ (1 + kT )s + k

T s2

+ (1 + kT )s + k

1

2

1

2

=

(T s2

+ s + k )(T s + 1)

=

.

T T s3

+ (T + T )s2

+ (1 + kT )s + k

1

2

1

2

1

2

2

Таким образом, µ = 0 (в ПФ нет интеграторов).

105

2.10. Инвариантные системы

Система называется инвариантной по отношению к входному сигналу, если по окончании переходного процесса, обусловленного ненулевыми начальными условиями, ошибка и регулируемая величина не зависят от этого входного сигнала.

Можно рассмотреть инвариантность системы относительно внешнего возмущения и относительно входного воздействия.

Для устранения ошибки, т.е. построения инвариантной системы, используется комбинированное уравнение, реализующее одновременно принципы регулирования как по отклонению, так и по возмущению.

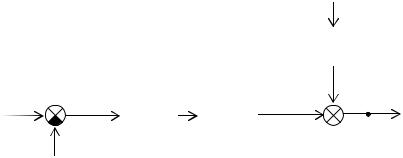
Рассмотрим систему, показанную на рис. 2.29, где F(s) – сигнал внешнего возмущения.

						F(s)
						W3(s)
						X2(s)
G(s)	E(s)				X1(s)			Y(s)
		W1(s)		W2(s)

Рис. 2.29. Система управления с шумом на выходе

Положим, что G(s) = 0, тогда для этой системы справедливо:

106

E(s) = −Y (s) ,

		1	(s) + X		2	(s) ,
Y (s) = X
X	1	(s) = W (s)W (s) E(s) ,
			1	2
X	2	( p) = W (s) F (s) .
				3

откуда

E(s) = −W1(s)W2 (s) E(s) − W3 (s) F (s) ,

(1+ W1(s) W2 (s)) E(s) = −W3 (s) F(s) .

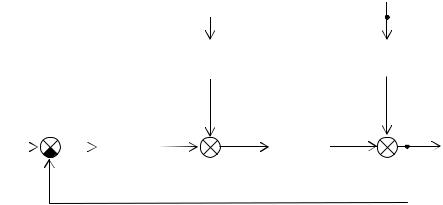
Для того чтобы поведение системы не зависело от внешнего возмущения, надо, чтобы правая часть этого уравнения была равна нулю. Помимо тривиального решения W3(s) = 0, здесь возможно введение второго канала передачи ошибки, компенсирующего влияние возмущения (рис. 2.30).

F(s)

W4(s)

W3(s)

B(s)

X2(s)

G(s) E(s)

A(s)

C(s)

X1(s)

Y(s)

W1(s)

W2(s)

Рис. 2.30. Инвариантная относительно возмущения система Для этой системы при условии G(s) = 0 справедливо:

107

E(s) = −Y (s) ,
Y (s) = X1 (s) + X 2 (s) ,
X		(s) =W (s) С(s) ,
	1	2
X 2 ( p) = W3 (s) F (s),
C(s) = A(s) + B(s),
A(s) = W1 (s)E(s),
B(s) = W (s)F (s) .
		4
Тогда

E(s) = −W2 (s)C(s) −W3 (s) F (s) =

= −W2 (s)W1 (s) E(s) −W2 (s)W4 (s) F (s) −W3 (s) F (s) ,

или

(1 + W1 (s)W2 (s))E(s) = −(W2 (s)W4 (s) + W3 (s))F (s) .

Таким образом, условие инвариантности ошибки относительно возмущающего воздействия:

W2 (s)W4 (s) + W3 (s) = 0.

Откуда следует выражение для ПФ второго канала:

W4 (s) = − W3 (s) = 0.

W2 (s)

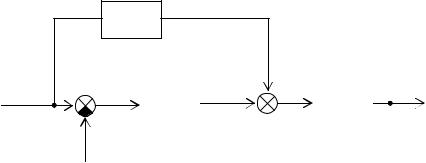
Рассмотрим далее систему, инвариантную относительно задающего воздействия. Здесь второй канал вводится способом, показанным на рис. 2.31.

108

B(s)

W3(s)

	G(s)	E(s)		A(s)	С(s)		Y(s)
			W1(s)			W2(s)

Рис. 2.31. Инвариантная относительно входного воздействия система

Для этой системы выполняется:

E(s) = G(s) − Y (s) ,
Y (s) = W (s)C(s) ,
	2
C(s) = A(s) + B(s) ,
A(s) = W (s) E(s),
	1
B(s) = W (s)G(s) .
	3

откуда

E(s) = G(s) − W2 (s)C(s) = G(s) − W1(s)W2 (s)E(s) − W2 (s)W3 (s)G(s).

(1+ W1(s) W2 (s)) E(s) = (1−W2 (s)W3 (s) )G(s) .

Тогда условие инвариантности относительно задающего воздействия приобретает вид

1 −W2 (s)W3 (s) = 0,

и второй канал должен иметь ПФ

109

W3 (s) =	1	.
	W2 (s)

На практике использовать это условие не всегда возможно, поскольку порядок числителя ПФ не должен превышать порядок знаменателя. Однако возможно приближенное решение, например:

W		(s) =	k		W (s) =	Ts + 1		≈	Ts +1		, T << T .
	2		Ts + 1						k (T1s +1)
					3	k					1

110