Конспект лекций по ТАУ

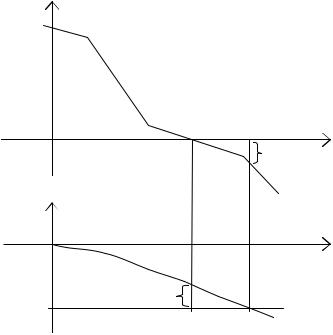
ЛФЧХ запас устойчивости по фазе – расстояние от значения фазы на частоте среза до уровня – π, и запас устойчивости по амплитуде – расстояние от оси частот ЛАЧХ до значения усиления на частоте, где фаза становится равной – π (рис. 4.19).

L(ω)

A ω

φ(ω)

ω

B

– π

Рис. 4.19. Запасы устойчивости по амплитуде (А) и по фазе (В).

Критерий устойчивости Найквиста для систем с запаздыванием

181

Формулировка критерия устойчивости Найквиста для систем с чистым запаздыванием аналогична формулировке для систем без запаздывания, имеющих дробно-рациональные передаточные функции. АФЧХ разомкнутой системы в этом случае:

W ( jω)e− jωτ = A(ω)e jϕ (ω)e− jωτ = A(ω)e j (ϕ (ω)−ωτ )

Из этого выражения видно, что звено запаздывания не меняет модуль А(ω) АФЧХ разомкнутой системы, а вносит лишь дополнительный отрицательный фазовый сдвиг ωτ, пропорциональный частоте ω с коэффициентом пропорциональности, равным времени запаздывания τ.

При построении АФЧХ разомкнутой системы с запаздыванием модуль A(ω) поворачивают на угол ωτ по часовой стрелке. С ростом частоты ω угол ωτ будет быстро расти, а модуль А(ω) обычно уменьшается, поэтому АФЧХ разомкнутой системы с запаздыванием имеет вид спирали, закручивающейся вокруг начала координат. Условие устойчивости ухудшается, так как вся АФЧХ приближается к критической точке (– 1, j0).

Можно найти критические значения времени запаз-

дывания τкр и соответствующие ему частоты ωкр, при которых W(jω)e– jωτ проходит через точку (– 1, j0).

Для этого случая запишем:

W ( jωкр )e− jωкрτкр = A(ωкр )e j (ϕ (ωкр )−ωкрτкр ) = −1.

Отсюда можно записать условия для амплитуд и фаз:

182

A(ωкр ) = 1;

φ(ωкр) – ωкрτкр = – π.

Из первого условия найдем ωкр , подставим это значение во второе уравнение и найдем допустимое минимальное значение τкр :

τкр = ϕ(ωкр ) + π , ωкр

где φ(ωкр) + π – запас устойчивости по фазе.

Обычно в целях повышения быстродействия и точности системы время запаздывания выбирают мини-

мальным: τ < τкр .

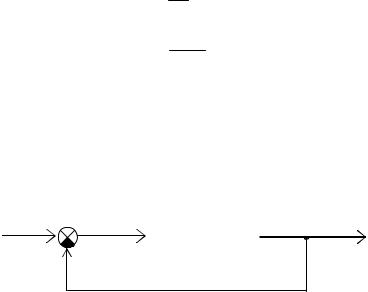
Пример 4.8. Найти значение τ, соответствующее границе устойчивости замкнутой системы, представленной на рис. 4.20.

183

X(s)	E(s)	e– τs		W (s) =	10		Y(s)
					s + 1

Рис. 4.20. Замкнутая система со звеном чистого запаздывания

Решение. Запишем передаточную функцию разомкнутой системы

W (s)e− τs =	10e− τs	,	W (s)e− jωτ =	10e− jωτ	.
	s +1			1+ jω

Найдем ωкр:

A(ωкр ) =			10		= 1	ωкр = 9 ,95;
			+ ωкр2
1
τкр = − arctg(9,95) + π ≈ 0,17.
				9,95

3. Частотные критерии качества

Запасы устойчивости

Частотные критерии качества наиболее разработаны в отношении определения запаса устойчивости, который можно определить по удалению АФХ разомкнутой системы от точки (– 1, j0) (рис. 4.21).

Запас устойчивости по амплитуде определяется точками a и c

184

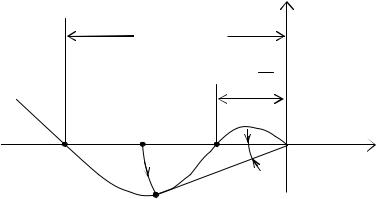
(см. рис. 4.21), которым соответствуют величины:

L1 = 20lg (β1) = 20lg(1/u1),

L2 = 20lg (β2) = 20lg(u2).

	u2 = β2		V(ω)
	u	=	1
	1	β
			1
	(– 1, j0)
c	a		U(ω)
		µ

b

Рис. 4.21. Определение запасов устойчивости

Запас устойчивости тем больше, чем больше L1 и L2. Запасом устойчивости по фазе называется величина

µ = 180 + φ,

где φ – аргумент частотной ПФ разомкнутой системы, соответствующий модулю, равному 1 (точка b).

Запас устойчивости также можно определять по показателю колебательности M.

Показателем колебательности называется максимальное значение ординаты Mmax амплитудной характеристики замкнутой системы при начальной ординате, равной 1, т.е. относительная высота резонансного пика (рис. 4.22).

Физический смысл показателя колебательности заключается в следующем. Если сигнал на входе системы меняется по закону

g(t) = gmax sin(ωt) ,

185

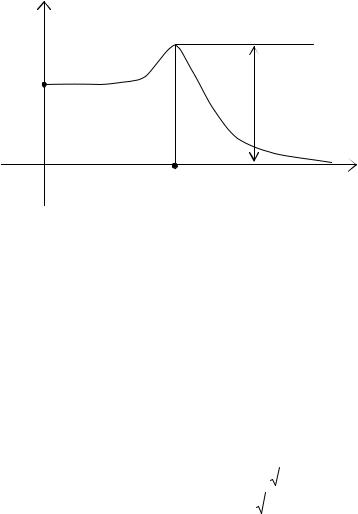
то на выходе будет сигнал

y(t) = ymax sin (ωt + φ) .

mod(W(jω))

1	Mma

ωp ω

Рис. 4.22. Определение показателя колебательности

Таким образом:

	ymax	=		W ( jω)		=	H ( jω)	,
	gmax						1 + H ( jω)

где W(jω) и H(jω) – ПФ замкнутой и разомкнутой системы.

M max	=		W ( jω)			=		H ( jω)		.
					max		1	+ H ( jω)
										max

Обычное требование Mmax < 1,1 ÷ 1,5.

Показатель колебательности можно отыскать по виду АФХ разомкнутой системы.

M =

=

H ( jω)

=

U + jV

=

U 2 + V 2

W ( jω)

.

1 + H ( jω)

1 + U + jV

(1 + U )2 + V 2

Если возвести в квадрат правую и левую часть и освободиться от знаменателя, то можно получить выражение:

186

(U + C )2 + V 2 = R2 ,
	M 2			M
C =		; R =			.
	M 2 − 1			M 2 − 1

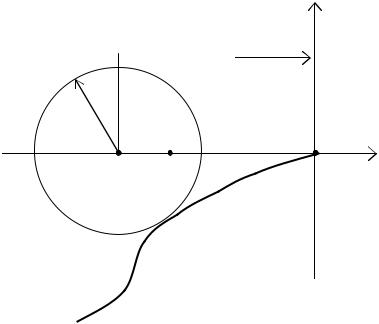
Таким образом получается уравнение окружности с центром, смещенным на С от начала координат и радиусом R.

Если задано условие на значение М, то достаточно, чтобы АФХ не заходила в запретную зону, заданную соответствующей окружностью (рис. 4.23).

jV

С

R

-1, j0

0 U

W(jω)

Рис. 4.23. Семейство окружностей, соответствующих разным значениям показателя колебательности

187

Точность при гармоническом воздействии

Пусть на вход системы поступает сигнал вида

g(t) = gmax sin(ωk t ).

Ошибка системы в установившемся режиме

e(t) = emax sin (ωk t + ϕ) .

Точность системы может быть оценена по амплитуде ошибки

emax = gmax						W ( jωk )			,
emax	=					gmax		.
			1	+ H ( jωk )

Обычно при проектировании emax << gmax, и на рабочей часто-

те

1 + H ( jωk ) >> 1.

Тогда

e ≈		gmax	=	gmax	,
max		H ( jωk )		A(ωk )

где A(ωk) - модуль частотной передаточной функции разомкнутой системы при ω = ωk.

Последнее выражение широко используется при расчёте систем методом ЛАХ. В этом случае модуль A(ωk) в дБ, т.е.

L(ωk ) = 20 lg A(ωk ) ,

равен ординате ЛАХ при частоте ω = ωk.

Для того чтобы амплитуда ошибки в системе не превосходила допустимого значения emax, ЛАХ должна проходить не ниже контрольной точки Ak с координатами

			g		max
L(ωk ) =							,
			20 lg A(ωk ) = 20 lg
			emax
ω = ω	k	.

188

Часто при проектировании и испытании систем управления пользуются синусоидальным задающим сигналом и в том случае, когда требования к системе поставлены по максимальной скорости и максимальному ускорению входного воздействия. В этом случае можно определить эквивалентный синусоидальный сигнал.

Если g(t) = gmsin(ωkt), то

g& = gmωk cosωk t

;

g&& = − gmω2k sin ωk t

Следовательно,

g&max = gmωk ;

g&&max = gmω2k .

Отсюда вычисляются частота ωk и амплитуда gm синусоидального задающего воздействия, соответствующие максимальной скорости и ускорению, а именно:

ωk = g&&m ;

g&m

gm = (g&m )2 . g&&m

Эти значения используются для нанесения координат контрольной точки на поле построения желаемой ЛАЧХ разомкнутого контура системы управления.

Пример 4.9. Найти амплитуду ошибки в системе, представленной на рис. 4.24.

G(s)	E(s)	H (s) =	k		Y(s)
			Ts + 1

189

Рис. 4.24. Замкнутая система при гармоническом воздействии

Входной сигнал

g(t) = gmax sin(ωk t ),

где gmax = 10, ωk = 2.

Передаточная функция замкнутой системы по ошибке

We

(s) =

1

=

1

=

Ts +1

,

+ H (s)

k

Ts +1+ k

1

1

+

Ts +1

=

Tjω +1

=

T 2ω2 +1

We

( jω)

.

Tjω+1+ k

T 2ω2 +1+ k

Пусть k = 20, Т = 0,1, тогда

	We ( jωk )		=			0,01× 4 +1			» 0,05.
					0,01× 4 + 20

emax = gmax W ( jωk ) = 10 ×0,05 = 0,5.

Сравним этот результат с приближенным значением:

e »		gmax	=	gmax T 2ω2 +1		» 0,5.
max		H ( jωk )			k

4.Синтез корректирующих устройств

Оценка качества следящей системы по виду ЛАЧХ разомкнутой системы

190