Конспект лекций по ТАУ

δ-функция (единичный импульс или функция Дирака) – это импульс, площадь которого равна единице при длительности, равной нулю, и высоте, равной бесконечности:

0	при	t < 0,
	при	t = 0,
δ(t) = ∞
	при	t > 0.
0

Согласно определению δ-функции справедливо:

∞

∫δ(t)dt = 1(t).

−∞

L(δ(t)) = 1.

Единичное рамповое воздействие (воздействие с постоянной скоростью).

x = t ×1(t); L(t ×1(t)) = 1 . s 2

Изменения во времени выходной величины звена (системы)

называют временными характеристиками звена (системы) или кривыми отклика.

Переходная характеристика – аналитическое выражение от-

клика звена на единичное ступенчатое входное воздействие при нулевых начальных условиях:

−1		1
h(t) = L	W (s)		.
		s

Произведение ПФ на изображение единичного ступенчатого воздействия, стоящее в квадратных скобках, соответствует изображению переходной характеристики. Графическое изображение переходной функции – кривая разгона.

71

Импульсная переходная характеристика (весовая функция) –

аналитическое выражение отклика звена на единичное импульсное входное воздействие при нулевых начальных условиях:

w(t) = L−1 (W (s) ×1) = L−1 (W (s)).

Графическое изображение импульсной переходной функции

– кривая веса.

Как нетрудно заметить:

sL(h(t)) = L(w(t)).

Таким образом, чтобы найти w(t), достаточно продифференцировать h(t).

Рамповая переходная характеристика – аналитическое вы-

ражение отклика звена на единичное рамповое входное воздействие при нулевых начальных условиях:

	−1		1
	x(t) = L	W (s)		.
			s 2

Переходная, импульсная переходная и рамповая переходная характеристики являются частными случаями временных характеристик (см. рис. 2.5).

Пример 2.11. Найти реакцию апериодического звена 1-го порядка при подаче на вход единичного ступенчатого воздействия и единичного импульса.

W (s) =

1

;

x(s) =

1

.

Ts + 1

s

−1

1 1

−1

A

B

−1

1

T

h(t) = L

=

L

+

=

L

-

=

(Ts +1) s

s

Ts +1

s

Ts +1

−1	1			−1		T			−	1	t
= L				- L					= 1(t) -1(t)e T .
	s				Ts +1

72

		dh(t)		1	−	1	t
	w(t) =		=		e T .
		dt		T

Пример 2.12. Дана переходная функция

h(t) = 1 + 2te−4t .

Определить ПФ.

Решение.

Переходная функция – это реакция на единичное ступенчатое воздействие:

h(t) = L−1 (W (s)x(s)),

где

x(s) =

1

.

s

1

2

h(t) = 1(t) + 1(t)2te

−4t = L−1

+

L−1

=

s

(s + 4)2

1 (s2

+ 10s + 16)

1

2

s2

+ 10s + 16

= L−1

+

= L−1

= L−1

.

2

2

2

s(s +

s

(s + 4)

4)

s (s

+ 8s + 16)

Таким образом:

W (s) =

s2 + 10s + 16

.

s2 + 8s + 16

Пример 2.13. Рассмотрим временные характеристики колебательного звена.

Передаточная функция колебательного звена

W (s) = k ,

T 2 s2 + 2ξTs + 1

где k – коэффициент усиления; T – постоянная времени; ξ – коэффициент затухания.

73

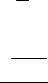
Колебательное звено меняет свои свойства и название в зависимости от величины ξ:

1)если 0 < ξ < 1, то звено называется колебательным, так как его временные характеристики носят колебательный характер;

2)если ξ ≥ 1, то звено называется апериодическим звеном второго порядка и колебания отсутствуют;

3)если ξ = 0, то звено называется консервативным (т. е. консервирующим колебания).

Определим переходную характеристику колебательного звена.

−1	1			−1			1
h(t) = L			W (s)	= kL					=
	s				s(T 2s2		+ 2Tξs + 1)

−1		1			T 2 s2 + 2Tξs
= kL			−						.
				(T	2		2
						s
	s							+ 2Tξs + 1)

Введем обозначение λ – показатель затухания:

λ = ξ ,

T

иω – угловая частота колебаний:

ω= 1 − ξ2 .

T

Тогда переходная характеристика равна

74

−1		1	1
h(t) = kL			−		2
	s			T

T 2 s2 + 2Tξs = ( + λ)2 + ω2 s

s +

ξ

1

ξ

ω

T

= kL−1

−

−

=

ωT (s + λ)2 +

s

(s + λ)2 + ω2

ω2

−1

1

s + λ

λ

ω

= kL

−

2

2 −

2

+ ω

ω

2

s

(s + λ)

(s + λ) + ω

λ

k 1

− e−λt cos(ωt ) −

e−λt

sin(ωt ) .

ω

Импульсная переходная характеристика

w(t) =	dh(t)	=	k	e− λt sin ωt.
			ωT 2
	dt

Пример 2.14. Временные характеристики консервативного звена.

Здесь λ = 0 и ω = 1/T, поэтому справедливо:

		λ
h(t) = k 1	− e− λt cos(ωt ) −		e− λt sin(ωt )	= k(1 − cos(ωt)),
		ω

w(t) = kωsin(ωt) = k sin(ωt).

T

2.5. Передаточная функция системы с обратной связью

Рассмотрим передаточную функцию одномерной системы с отрицательной обратной связью (рис. 2.7, где W – передаточная функция разомкнутой системы; WOC – передаточная функция обратной связи).

75

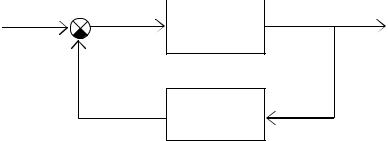
g(t)

e(t)

y(t)

W

yoc(t)

WOC

Рис. 2.7. Система с отрицательной обратной связью

Здесь справедливы следующие зависимости:

y(s) = W (s)e(s),

yOC (s) = WOC (s) y(s), e(s) = g(s) − yOC (s), g(s) = e(s) + yOC (s).

Тогда ПФ замкнутой системы Wз получается по формуле:

W (s) =

y(s)

=

W (s)e(s)

=

W (s)

=

W (s)

=

з

g(s)

e(s) + y (s)

1

+

yOC (s)

y(s)

OC

e(s)

1 + WOC e(s)

=

W (s)

.

1 + WOC (s)W (s)

При положительной обратной связи в знаменателе сумма превратится в разность.

Если отрицательная обратная связь единичная, то
Wз (s) =	y(s)	=	W (s)	.	(2.5)
	g(s)		1 + W (s)

76

Формула (2.5) показывает, что коэффициент усиления замкнутой системы меньше коэффициента усиления разомкнутой системы.

Рассмотрим вариант, когда WOCW >> 1, тогда

Wз (s) =		W (s)	»	1		,
		+ WOC (s)W (s)
1				WOC (s)

и выходной сигнал

y(s) = 1 g(s).

WOC (s)

При WOC = 1 выходной сигнал становится равным входу, однако условие WOCW >> 1 может привести к потере устойчивости системы.

Таким образом, введение обратной связи позволяет сформировать сигнал, пропорциональный ошибке управления, так что уменьшается влияние изменений параметров объекта управления на выходной сигнал, т.е. снижается чувствительность системы управления.

Чувствительность системы S определяется как отношение процентного изменения ПФ системы к процентному изменению ПФ объекта.

Передаточная функция системы равна отношению выходного сигнала к входному:

WS = Y (s) .

G(s)

Поэтому чувствительность разомкнутой системы S = 1. Для замкнутой системы:

	WS (s) /WS (s)		∂WS (s) /WS (s)		∂WS (s)	W (s)
S =	DW (s) /W (s)	=	¶W (s) /W (s)	=	¶W (s) ×		.
						W (s)
						S

Поскольку

77

	WS (s) =			W (s)
						,
		1 + WOC (s)W (s)
Получаем
	¶WS (s) W (s)			1
S =	¶W (s) ×			=			.
		WS (s)			1 + WOC (s)W (s)

Часто бывает нужно определить чувствительность относительно параметра α ПФ объекта W(s). Здесь можно использовать формулу:

Sα =	¶WS /WS	=	¶WS	×	α	.
	¶α/ α		¶α WS

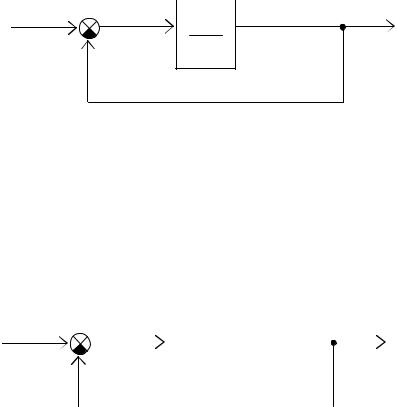
Пример 2.15. Рассмотрим систему с обратной связью, показанную на рис. 2.8.

g(t)

e(t)

y(t)

1

s + α

Рис. 2.8. Система с варьируемым параметром α

Здесь

	(s) =	1			Sα = -	α
WS				,			.
		s + α +1
						s + α +1

Пример 2.16. Исследуем чувствительность системы 2-го порядка относительно коэффициента усиления К (рис. 2.9).

g(t)	e(t)				y(t)
78			K
			s2 + s

Рис. 2.9. Система с варьируемым коэффициентом усиления

WS (s) =	K		SK = −	s2 + s
		,			.
	s + α + K			s2 + s + K

Исследования чувствительности выполняются при проектировании робастных систем, сохраняющих высокое качество функционирования при наличии неопределенных факторов.

2.6.Частные передаточные функции

Всоответствии с принципом суперпозиции, можно выразить любой выходной сигнал линейной системы через любой входной сигнал при условии, что все остальные входные сигналы равны нулю и имеются нулевые начальные условия.

Рассмотрим одноконтурную систему, т.е. такую систему, у которой при размыкании в какой-либо точке замкнутого контура получается цепь без параллельных и обратных соединений (рис.

2.10).

79

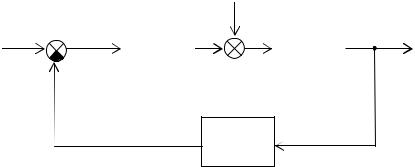
				F(s)
	U(s)	E(s)				Y(s)
			W1(s)		W2(s)

Yoc(s)

Woc(s)

Рис. 2.10. Система управления с обратной связью

Цепь по ходу сигнала от точки приложения входного сигнала до точки съема выходного сигнала называется прямой цепью. Прямая цепь представляет собой последовательное соединение звеньев, включая сумматоры (передаточная функция сумматора по входу плюс равна единице, а по входу минус – минус единице). На рис. 2.12 для входного сигнала U(s) и выходного

сигнала Y(s) прямая цепь W1(s)W2(s).

Существует правило вычисления ПФ замкнутой одноконтурной системы: передаточная функция Wxy одноконтурной системы относительно внешнего воздействия x и выхода y равна ПФ прямой цепи, деленной на единицу минус ПФ контура:

Wxy (s) =	Y (s)	=		WП (s)
					.
	X (s)
			1 − WK (s)

Главная ПФ или ПФ замкнутой системы:

Wзс (s) =	Y (s)	=		W1 (s)W2	(s)
						.
	U (s)
			1 + W1 (s)W2 (s)Woc (s)

При нулевом входном сигнале U(s) = 0, ПФ по возмущению (от возмущения к выходу). Рис 2.10 преобразуется к виду, приведенному на рис. 2.11.

80