Конспект лекций по ТАУ

		k					T1ω
A(ω) =			, ϕ(ω) = − arctg								.
							2
		2							2
		(1− T22ω2 ) + T12ω2			1		− T2	ω
L(ω) = 20 lg A(ω) = 20 lg k − 20 lg
				(1 − ω2T 2 )2			+ T 2	ω2 .
			2				1

При ω → 0:

L(ω) → 20 lg k .

При ω → ∞ наибольшее значение имеет член при ω4:

L(ω) → 20 lg k − 40 lg(T2ω)→ −∞.

Для вычисления наклона прямой опять рассмотрим изменение усиления в границах одной декады:

10

1

L(ω) = L

− L

=

T

T

10

1

= 20 lg k −

40 lg

T

−

20 lg k − 40 lg

T

= −40.

T

T

Наклон асимптоты оказывается равным –40 дБ/дек. Излом ЛАЧХ происходит на частоте ω = 1/T2. Запишем АЧХ колебательного звена в виде

A(ω) =		k
				.
		(1 − T 2ω2 )2 + (2ξTω)2

При коэффициенте затухания ξ = 0 и T2 = 1/ω2 коэффициент усиления звена становится бесконечным. В реальности при малых ξ в районе частот, близких к ω = 1/T2, наблюдается резонансный пик (рис. 4.6).

A

161

ω = 1

ω

T

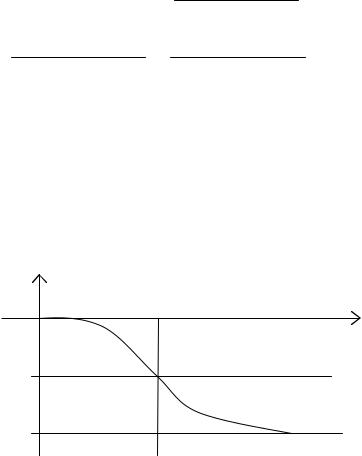
Рис. 4.6. АЧХ колебательного звена

Выделим в ПФ вещественную и мнимую часть:

				k
	W ( jω) =							=
			-T 2ω2 +1+ 2ξTωj
			k				((1-T 2ω2 )- 2ξTωj)
=					×		((1-T 2ω2 )- 2ξTωj)		=
		(1-T 2ω2 ) + 2ξTωj
=	k(1-T 2ω2 )			- j				2ξTωk		= .
	(1-T 2ω2 )2 + (2ξTω)2					(1-T 2ω2 )2 + (2ξTω)2

= U (ω) - jV (ω).

По определению ФЧХ определяется согласно формуле

	V (ω)			2ξTω
ϕ (ω) = arctg		= arctg	−		.
				1 − T 2ω2
U (ω)

Тогда w = 0, φ(w) = 0; w = 1/T, φ(w) = – π/2; w =¥, φ(w) = –

π.

График ФЧХ колебательного звена показан на рис. 4.7.

φ

ω =1/T

ω

162– π/2

–π

Рис. 4.7. ФЧХ колебательного звена

Таким образом, колебательное звено, как и все инерционные звенья, хорошо пропускает сигналы низкой частоты и плохо – сигналы высокой частоты; если частота гармонического входного сигнала близка к частоте собственных колебаний звена, то отношение амплитуды выходного сигнала к амплитуде входного больше коэффициента усиления k.

Пример 4.4. Рассмотрим ЛАЧХ и ЛФЧХ идеального дифференцирующего и идеального интегрирующего звеньев.

Идеальное дифференцирующее звено:

W ( jω) = jωk,
A(ω) = kω,
kω				π
ϕ (ω) = arctg			=		,
0				2

L(ω) = 20 lg(kω) = 20 lg(k )+ 20 lg(ω).

Очевидно, L(ω) = 0 при ω = 1/k.

Рассматривая границы одной декады, можно записать

10

1

L(ω) = L

− L

=

T

T

1

1

= 20 lg k +

20 lg 10

−

20 lg k + 20 lg

= 20.

T

T

163

Наклон оказывается равным 20дБ/дек. Аналогично для идеального интегрирующего звена:

W ( jω) =

k

= − j

k

,

ω

jω

A(ω) =

k

,

ω

− k / ω

π

ϕ (ω) = arctg

= −

,

0

2

k

L(ω) = 20 lg

= 20 lg(k )− 20 lg(ω).

ω

Очевидно, L(ω) = 0 при ω = k.

Рассматривая границы одной декады, можно записать

10

1

L(ω) =

L

− L

=

T

T

1

1

20 lg k − 20 lg 10

−

20 lg k − 20 lg

= −20.

T

T

Наклон равен –20 дБ/дек.

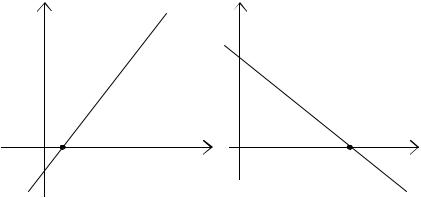
Графики ЛАЧХ показаны на рис. 4.8.

а)

б)

L(ω)

L(ω)

+20 дБ/дек

-20 дБ/дек

164

1

ω

ω = k

ω

ω =

k

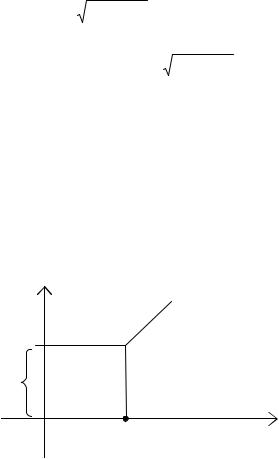
Рис. 4.8. ЛАЧХ идеального дифференцирующего (а) и идеального интегрирующего (б) звеньев

Пример 4.5. ЛАЧХ и ЛФЧХ форсирующего звена:

W ( jω) = k (1 + k1 jω),
A(ω) = k	(1 + k 2ω2 )	,
1
ϕ (ω) = arctg (k1ω),			(1 + k 2	ω2 )
L(ω) = 20 lg(k )+ 20 lg					.
			1
При ω → 0:
L(ω) → 20 lg k .
При ω → ∞:

L(ω) → 20 lg(k1ω)→ ∞.

Таким образом, форсирующее звено близко к идеальному усилительному на низких частотах и к дифференцирующему – на высоких частотах (рис. 4.9).

L(ω)

+20 дБ/дек

20lgk

ω =	1	ω	165

k

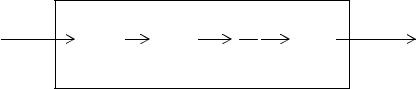
Рис. 4.9. ЛАЧХ форсирующего звена

4.3. Частотные характеристики разомкнутой системы

Рассмотрим последовательное соединение динамических звеньев (рис. 4.10).

x						y
	W1		W2		Wn
				W

Рис. 4.10. Последовательное соединение передаточных функций

Поскольку ПФ можно рассматривать как комплексное число, имеем

n

W ( jω) = A(ω)e jΨ (ω) = ∏ Ai (ω)e

i =1

n

j ∑ϕ i (ω)

i =1 ,

где Ai и φi – амплитудная и фазовая характеристика каждого звена.

Таким образом:

n

A(ω)= ∏ Ai (ω).

i=1

Ψ(ω) = n ϕ (ω)

∑i .

i=1

166

Для ЛАЧХ получается:

20lg A(ω) = 20lg A1 (ω)+ 20lg A2 (ω)+ ...+ 20lg An (ω).

Всоответствии с этой формулой методика построения ЛАЧХ

восновном сводится к суммированию ординат.

Разомкнутая динамическая система может быть представлена как совокупность последовательно соединенных типовых звеньев.

Алгоритм построения ЛАЧХ разомкнутой системы включает

всебя следующие шаги:

1.определяются сопрягающие частоты типовых

звеньев в порядке возрастания: ω1, ω2,… ωn , и помечаются на оси частот;

2.вычисляется при частоте ω =1 ордината 20lgK, где K – общий коэффициент передачи разомкнутой системы. Через полученную точку проводится низкочастотная

асимптота ЛАЧХ, представляющая собой при ω < ω1 прямую с наклоном – λ20 дБ/дек, где λ – количество интегрирующих звеньев;

3.изменение наклона ЛАЧХ L(ω) на сопрягающих

частотах ωi по сравнению с тем наклоном, который она имела до рассматриваемой частоты, происходит по правилу: для апериодического звена наклон изменяется на – 20 дБ/дек, для колебательного – на –40 дБ/дек, для форсируюшего – на +20 дБ/дек.

167

Пример 4.6. Построим ЛАЧХ система, ПФ которой в разомкнутом состоянии имеет вид:

W ( jω) = k (T2 s + 1) .

(T1s + 1)2 (T3s + 1)

Таким образом, ЛАЧХ и ЛФЧХ системы описываются формулами:

L(ω)= 20 lg k − 40 lg 1 + T12ω2 + 20 lg 1 + T22ω2 − 20 lg 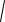1 + T32ω2 .

Ψ(ω) = −2arctg(T1ω) + arctg(T2ω) − arctg(T3ω). .

Пусть ПФ имеет следующие параметры: k = 100, T1 = 1 с, T2 = 0,2 с, T3 = 0,005 с. Тогда сопрягающие частоты:

ω =

1

= 1 c−1;

ω

=

1

= 5 c−1;

ω

=

1

= 200 c−1.

2

3

1

T1

T2

T3

Поскольку ПФ не содержит интегрирующих звеньев, начальный участок ЛАЧХ будет параллелен оси частот, затем на частоте ω = 1 наклон изменится на –40 дБ/дек, на частоте ω = 5 наклон изменится на +20 дБ/дек, и на частоте ω = 200 – на –20

дБ/дек (рис. 4.11).

L(ω)

40	–40 дБ/дек

20lg(k

ω3

ω1 ω2 10

100

1000 ω

168

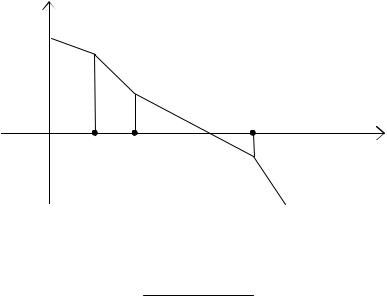
Рис. 4.11. Пример построения ЛАЧХ разомкнутой системы Пример 4.7. Определить, какая ПФ соответствует системе,

ЛАЧХ которой показана на рис. 4.12.

L(ω)

60 –20 дБ/дек

	–40	дБ/дек
		–20 дБ/дек
1	1.	2	ω
		–60	дБ/дек

Рис. 4.12. Пример построения ЛАЧХ разомкнутой системы

Ответ:

W (s) = 1000(0,83s +1) . s(s +1)(0,5s +1)2

4.4. Частотные критерии устойчивости

Критерий устойчивости Михайлова

Пусть известно характеристическое уравнение системы

A(s) = ansn +an−1sn−1 +×××+a1s +a0.

Если сделать замену s = jω, то получается уравнение ком-

169

плексного вектора

A( jω) = an ( jω)n +an−1( jω)n−1 +×××+a1( jω)+a0 =U(ω) + jV(ω).

При изменении частоты ω от 0 до ∞ этот вектор описывает некоторую кривую – кривую Михайлова.

Кривая Михайлова начинается при ω = 0 в точке U(0) = a0 и заканчивается в n-ом квадранте при ω = ∞ (если отсчет квадрантов вести против часовой стрелки), где уходит в бесконечность.

Таким образом, чтобы построить кривую Михайлова, надо в характеристическом уравнении заменить s на jω и разделить вещественную и мнимую часть. Далее, задавая различные значения частоты, найти точки с координатами:

{U(0); jV(0)}{, U(ω1); jV(ω1)}{, U(ω2 ); jV(ω2 )}...

По этим точкам строится кривая Михайлова.

Критерий устойчивости Михайлова: линейная система n-го порядка будет устойчива, если кривая Михайлова охватывает начало координат, и последовательно проходит n квадрантов против часовой стрелки.

Если кривая Михайлова проходит через начало координат, то система находится на границе устойчивости.

На рис. 4.13 показаны примеры кривой Михайлова для системы 6-го порядка.

	a)		б)
	jV(ω)		jV(ω)
	ω → ∞	ω2	ω → ∞
				ω2
	ω3	ω1	=
				ω1	=
		a0	U(ω)	a0	U(ω)
				ω3

170