Конспект лекций по ТАУ

u(t) = L di(t) + Ri(t), dt

которое в изображениях по Лапласу приобретает вид

U (s) = LsI(s) + RI(s) = I (s)(Ls + R).

Передаточная функция между входом и выходом схемы:

W (s) =	I (s)	=	1	=	1 R	=	k	,
					(L / R)s + 1
	U (s)		Ls + R				Ts + 1

где k = 1/R – коэффициент передачи, T = L/R – постоянная времени.

Для схемы на рис. 2.1, б будем считать входной величиной напряжение u1, а выходной – u2. При расчете передаточной функции должны выполняться два условия:

−цепь не нагружена (никаких элементов к выходным зажимам не подключено, либо эти элементы имеют сопротивление, стремящееся к бесконечности);

−сопротивление источника входного напряжения настолько мало, что им можно пренебречь.

u1 (t) = i(t)R + uc (t),
	(t) = uc (t),
u2
		duc (t)
i(t) = C			.
		dt

Переходя к изображениям по Лапласу, имеем

U1 (s) = (RCs + 1)Uc (s),U 2 (s) = Uc (s).

Передаточная функция

61

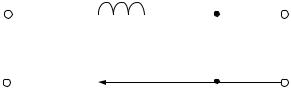
U2 (s)			Uc (s)	1
W (s) =		=		=		,
	U1 (s)		(RCs +1)Uc (s)		Ts +1

где T = RC –	постоянная времени.
Рассмотрим далее ПФ для RLC-цепи, показанной на рис. 2.3.
			R		L
u1										u2
						C
					i

Рис. 2.3. RLC-цепь Здесь справедливы соотношения:

u (t) = i(t)R + L					di	+ u		(t),
							c
	1				dt
		1
			∫	idt ,
		C
uc (t) =

u2 (t) = uc .

Преобразование Лапласа дает:

1

U1

(s) =

I (s) R + Ls +

,

sC

1

(s) =

I (s).

U

2

sC

W (s) =

U 2 (s)

=

1

=

1

.

U

(s)

LCs2 + RCs + 1

T s

2 + T s + 1

1

1

2

62

Пример 2.9. Рассчитает закон изменения выходного напряжения при известных параметрах RLC- цепи и известном входном напряжении.

Дано: u1 = 10 В, R = 3 Ом, L = 1 H, C = 0.5 Ф. Найти u2(t).

Решение.

W (s) =

U 2

(s)

=

1

=

2

.

U1

(s)

0.5s2 + 1.5s + 1

(s + 1)(s + 2)

U 2 (s) = U1 (s)W (s) =

20

=

10

−

20

+

10

.

s(s + 1)(s + 2)

s s + 1 s +

2

u2 (t) = 10 − 20e−t + 10e−2t .

Рассмотрим далее построение ПФ для механической системы с линейным перемещением y(t) (рис. 2.4).

63

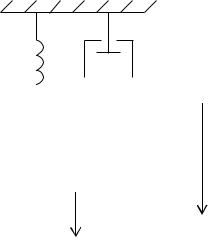
fПР= –k 1y(t)	fТР= –k 2dy(t)/dt

					y
	M
		f(t)

Рис. 2.4. Механическая система с линейным перемещением

На тело массой M действует три силы: внешняя сила f(t), сила трения fТР(t), пропорциональная скорости, и сила упругости пружины fПР (t), пропорциональная перемещению.

Под действием этих сил тело массой M движется согласно закону Ньютона, который гласит, что сумма сил, действующих на тело, равна произведению массы тела на его ускорение:

M	d 2 y(t)		= f (t) − k				dy(t)			− k y(t),
	dt 2					2 dt			1
а передаточная функция
W(s) =			Y(s)	=		1					.
					Ms 2 + k
			F(s)					2	s + k
									1

Это выражение определяет зависимость положения y(t) от действующей силы f(t).

Как показали приведенные примеры для RLC-цепи и механической системы с линейным перемещением, разным по своей

64

физической природе объектам может соответствовать одна и та же ПФ. Этим определяется универсальный характер аппарата ПФ.

2.3. Типовые динамические звенья

Поскольку произвольный полином можно разложить на множители, сложную ПФ можно представить в виде произведения простых ПФ с порядком не выше 2-го. Такие простые ПФ назы-

вают элементарными или типовыми (табл. 2.3).

Таблица 2.3

Типовые динамические звенья

№

Название звена

ПФ звена

1

Интегрирующее

W (s) =

k

s

2

Дифференцирующее

W (s) = ks

Усилительное

W (s) = k

3

(безынерционное)

Апериодическое 1 -го

k

4

порядка

W (s) =

(инерционное)

Ts +1

Апериодическое 2-го

порядка

W (s) =

k

; T1

³ 2T2

5

(все корни вещест-

T

2

s

2

+ T s + 1

2

1

венные)

65

Продолжение табл. 2.3

6

Колебательное*

W (s) =

k

; T1 < 2T2

T 2 s 2

+ T s + 1

2

1

7

Консервативное

W (s) =

k

Ts2

+ 1

Интегрирующее с за-

паздыванием

W (s) =

k

8

(реальное интегри-

s(Ts

+ 1)

рующее)

Дифференцирующее

9

с запаздыванием

W (s) =

ks

(реальное дифферен-

Ts + 1

цирующее)

10

Форсирующее

W (s) = k(Ts + 1)

11

Изодромное

W (s) =

k (Ts + 1)

s

12

Звено с чистым запаз-

W(s) = e−τs

дыванием

* часто используется описание колебательного звена в виде

W (s) =		K		; T = T ,	ξ =	T1	.
	T 2 s2	+ 2ξTs + 1
				2		2T
					2

Большинство реальных динамических объектов допускает описание с помощью ПФ первого или второго порядка (возможно – с запаздыванием), так что типовое описание объекта управления имеет вид

66

	W ( p) =	k exp(−τs)	;	T1 > 2T2 .	(2.1)
		(T1s + 1)(T2 s + 1)

Для объектов управления с явно выраженной преобладающей постоянной времени передаточная функция упрощается

W ( p) =	k exp(−τs)	,	(2.2)
	Ts + 1

где K, T, τ – коэффициент усиления, постоянная времени и запаздывание, которые должны быть определены в окрестности номинального режима работы объекта.

Для объекта управления без самовыравнивания передаточная функция имеет вид

W (s) =	ke− τs	.	(2.3)
	s

Рассмотрим метод касательной – экспериментальный метод определения временных динамических характеристик объекта управления (2.2), который предполагает подачу на вход объекта пробного тестирующего сигнала – прямоугольного ступенчатого сигнала. Кривая переходного процесса (кривая разгона) показана на рис. 2.5.

Коэффициент усиления k показывает, во сколько раз данное звено усиливает входной сигнал, таким образом:

k = yуст .

g

Точка перегиба соответствует переходу кривой от режима ускорения к режиму замедления темпа нарастания выходного сигнала. Постоянная времени Т определяется в соответствии с графиком рис. 2.5.

67

y(t), g(t)

yуст

0.63yуст

0.1yуст

τз τ

y(t)

g(t)

τ0.

t

T

Рис. 2.5. Кривая разгона динамического объекта

Достаточно точной считается также оценка вида:

T = τ0.63 − τз .

Динамическое запаздывание τ также определяется по графику, и складывается из двух компонент:

τ = τз + τd,

где τз – чистое (емкостное) запаздывание; τd – транспортное запаздывание.

Для объекта без самовыравнивания вида (2.3) динамический коэффициент усиления K определяется как отношение установившейся скорости изменения выходной величины y к величине скачка входного сигнала. При единичном скачке:

68

k = y . t

Таким образом, при описании апериодического звена 1-го порядка используются два коэффициента, которые имеют четкий физический смысл: K – коэффициент усиления; T – постоянная времени.

При описании колебательного звена также желательно иметь параметры, отражающие физический смысл. С этой целью применяется следующая форма записи:

ω 2
n
W ( p) = s2 + 2ξωn s + ωn2 .	(2.4)

где ξ – безразмерный коэффициент затухания; ωn – собственная частота колебаний (частота при отсутствии затухания).

Пример 2.10. Дана ПФ колебательного звена:

	W (s) =			1425				.
		s2 + 20s +
						1500
Требуется записать ПФ в форме (2.4).
Решение.
	ω2 = 1500				ω = 38,73 .
	n				n
	2ξωn = 20				ξ = 0,258 .
Таким образом,
1425								ω2
W (s) =				= 0,95				n
									.
	s2 + 20s + 1500						s2 + 2ξωn s + ωn2

Наиболее универсальным алгоритмом определения параметров модели следует признать метод наименьших квадратов (МНК). С его помощью можно построить модель не только второго, но и более высоких порядков. Для использования МНК

69

необходимы массивы значений входных и выходных сигналов объекта, снятых через некоторый интервал времени (период квантования).

2.4.Временные характеристики

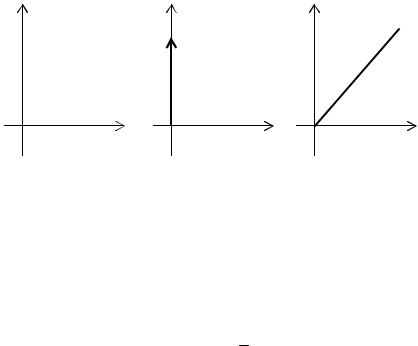
Одинамических свойствах звена (или системы) судят по реакции на типовые входные воздействия (единичное ступенчатое (рис. 2.6, а), единичное импульсное (рис. 2.6, б), с постоянной скоростью – рамповое (рис. 2.6, в) и т. д.).

a)		б)	в)
1(t)		δ(t)	x(t)
		∞
1

0	t	0	t	0	t

Рис. 2.6. Типовые входные воздействия

Единичное ступенчатое воздействие (единичная функция или функция Хевисайда) – это воздействие, которое мгновенно возрастает от нуля до единицы и далее остается неизменным:

0	при	t < 0,
1(t) =		t ³ 0.
1	при

L(1(t)) = 1 . s

70