Расчет поступательно движущихся систем
Определим напряжения в канате грузоподъемного механизма, к которому подвешен груз массой m (рисунок 15.2).
При равномерном подъеме с постоянной скоростью ускорение движения груза равно нулю, поэтому напряжения в канате такие же, как и в том случае, когда груз висит на канате в состоянии покоя, т. е. σ=mg/G, где g - ускорение силы тяжести.
Рисунок 15.2.
Во время разгона движение груза неравномерно, и в канате появляются дополнительные напряжения, для определения которых мысленно остановим груз и приложим к нему силу инерции. Эта сила направлена в сторону, противоположную движению груза и равна
,
где v - скорость подъема; w - ускорение.
Наибольшее усилие в канате соответствует моменту максимального ускорения груза во время разгона:
.
Следовательно, максимальное напряжение в канате при подъеме груза
.
больше напряжений при статическом приложении груза σcn=mg/F в kд раз; коэффициент
называется динамическим коэффициентом.
Таким образом, для уменьшения растягивающего усилия в канате необходимо обеспечить плавное увеличение скорости подъема, так как при больших ускорениях напряжения в канате могут стать значительными. График изменения скорости в период разгона должен иметь вид, представленный на рисунок 14.3. Тангенс наибольшего угла α наклона касательной к этой кривой определяет максимальное ускорение движения груза во время подъема.
Рисунок 14.3.
При опускании груза в начале движения величина w=dv/dt в выражении для kд будет иметь отрицательный знак. Следовательно, напряжения в канате в этом случае будут меньше напряжений от статического действия груза m.
Если канат длинный, то следует учесть массу самого каната и силы инерции его частиц. В этом случае опасным будет верхнее сечение каната, усилие в котором
,
где x - длина каната; ρ - плотность материала каната.
Рассмотрим горизонтальный брус, поднимаемый вверх силой S, приложенной посредине бруса (рисунок 14.4,а).
Интенсивность полной погонной нагрузки, состоящей из собственного веса q бруса и инерционной нагрузки pi, определяется по формуле (рисунок 14.4, б, в)
или
,
где G - вес бруса, w - ускорение бруса.
Рисунок 14.4.
Сила S и нагрузка qсумм вызывают изгиб бруса. Эпюры изгибающих моментов M и поперечных сил Q показаны на рисунок 14.4, г, д.
Напряжения в тонкостенном вращающемся кольце
Рассмотрим случай вращения тонкостенного кольца (δ<<R) с постоянной угловой скоростью ω вокруг оси, перпендикулярной к плоскости кольца (рисунок 14.5, а).
При вращении кольца каждый его элемент движется с центростремительным ускорением j=ω2R. Силы инерции направлены в сторону, противоположную ускорениям, и при постоянном сечении распределены равномерно вдоль кольца. Интенсивность сил инерции, т. е. сила инерции, приходящаяся на единицу длины кольца, q=Fρω2R. Здесь ρ - плотность материала, F - площадь сечения, а R - радиус средней линии кольца.
Кольцо теперь можно рассматривать как неподвижную плоскую раму, нагруженную равномерно распределенными радиальными силами интенсивностью q.
Рассекая кольцо любой диаметральной плоскостью на две части, приложим в сечениях осевые силы N и изгибающие моменты X1.
Рисунок 14.5.
Проектируя все силы, действующие на полукольцо, на направление оси y, получаем
.
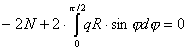Отсюда
.
Подставляя в это выражение значение q, находим
.
Для определения неизвестного X1 составим каноническое уравнение
,
коэффициенты которого вычислим способом Мора.
Изгибающий момент в текущем сечении полукольца от силы N и распределенной нагрузки q (см. рисунок 14.5, б)
,
а от единичной пары M1j=+1.
Следовательно, δ1P=0 и поэтому X1=0, т. е. изгибающие моменты во всех поперечных сечениях кольца равны нулю. Этот результат объясняется тем, что при вращении вокруг центра кольцо сохраняет свою форму и никаких изгибных деформаций не испытывает; увеличивается только его диаметр.
Таким образом, нормальные напряжения в поперечном сечении кольца
|
(14.2) |
.Например, в стальном кольце (ρ=7850 кг/м3) радиуса R=50 см при n=2500 об/мин растягивающее напряжение
Итак, напряжения во вращающемся кольце зависят только от окружной скорости v=ωR и плотности материала, но не зависят от площади его поперечного сечения. Поэтому увеличением размеров сечения нельзя уменьшить напряжения в тонкостенном вращающемся кольце.
Рассмотрим теперь случай равномерного вращения тонкостенного кольца вокруг его горизонтальной оси x.
Различные элементы кольца находятся на разных расстояниях от оси вращения, и поэтому силы инерции распределены неравномерно по длине кольца (рисунок 14.6, a):
.
Максимальная интенсивность q=ρFω2R. Следовательно,
.
В сечениях вдоль вертикальной оси симметрии кольца будут действовать только изгибающие моменты X1, а перерезывающие силы Q и нормальные силы N равны нулю. В отсутствии нормальных сил N в этих сечениях легко убедиться, спроектировав все силы, действующие на левое или правое полукольцо, на горизонтальную ось симметрии.
Представим эквивалентную систему, как показано на рисунок 14.6,б. Изгибающий момент в текущем сечении кольца от внешней нагрузки
,
а от единичной пары M1j+1.
|
Рисунок 14.6. |
Рисунок 14.7. |
Составим каноническое уравнение
,
Коэффициенты δ1P и δ11 этого уравнения:
;
.
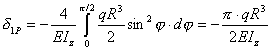Следовательно,
.
Итак, изгибающий момент в текущем сечении рамы
.
Эпюра изгибающих моментов представлена на рисунок 14.7. Опасными являются сечения A и B кольца, так как в этих сечениях кроме изгибающих моментов M=qR2/4 действуют наибольшие растягивающие нормальные силы
.
Максимальные напряжения в раме
,
где Wz - момент сопротивления изгибу, а F - площадь поперечного сечения кольца.