
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота № 1 Властивості визначників. Обчислення визначників за допомогою їх властивостей.
- •Вправи для самостійної роботи
- •Індивідуальні завдання №1
- •Самостійна робота № 2 Ранг матриці та способи його обчислення.
- •Приклади розв’язання типових задач.
- •Самостійна робота № 3 Обернена матриця
- •Матричні рівняння.
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання №3
- •Самостійна робота № 4
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 4
- •Самостійна робота № 5
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 5
- •Самостійна робота № 6
- •Основні теоретичні відомості
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 6
- •Самостійна робота № 7 вектори
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Самостійна робота № 8
- •Приклади розв’язання типових задач.
- •Вправи для аудиторної роботи.
- •Індивідуальні завдання № 7
- •Індивідуальні завдання №8
- •Основні теоретичні відомості
- •Приклади розв’язання типових задач.
Приклади розв’язання типових задач.
1.
Дано точки
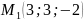 ,
,
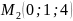 .
Знайдіть:
.
Знайдіть:
а)
координати, довжину, напрямні косинуси
та орт вектора
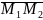 ;
;
б)
координати точки М, яка ділить відрізок
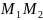 у відношенні
у відношенні
 .
.
Розв'язання.
а)
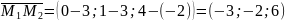
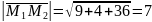 ;
;
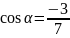 ,
,
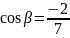 ,
,
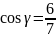 .
.
Орт вектора такий:
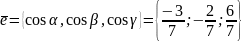 .
.
б)
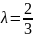 ,
тоді
,
тоді
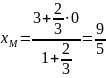 ,
,
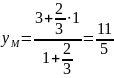 ,
,
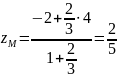 .
.
2.
Знайдіть вектор
,
якщо він утворює з осями координат
однакові кути і
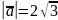 .
.
Розв'язання. Враховуючи рівності
 ,
,
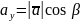 ,
,
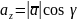
і
умову
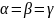 ,
записуємо співвідношення
,
записуємо співвідношення
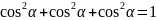 ,
,
звідки
дістаємо
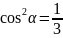 ,
,
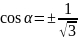 ,
,
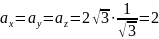 або
або
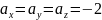 .
.
Відповідь:
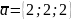 або
або
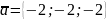 .
.
3.
Чи колінеарні вектори
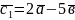 і
і
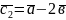 побудовані на векторах
побудовані на векторах
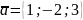 і
і
 ?
?
Розв'язання. Послідовно дістаємо
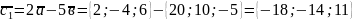
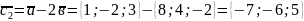 .
.
Оскільки
координати векторів
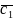 і
і
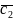 не пропорційні, то ці вектори не
колінеарні.
не пропорційні, то ці вектори не
колінеарні.
4.
Початком вектора
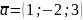 є точка
є точка
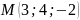 .
Знайдіть координати точки Р, яка є кінцем
вектора
.
.
Знайдіть координати точки Р, яка є кінцем
вектора
.
Розв'язання. Враховуючи умову рівності двох векторів, дістанемо
 ,
,
або
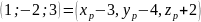
звідси
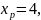
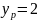 ,
,
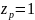 ,
тобто
,
тобто
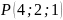 - кінець вектора
.
- кінець вектора
.
5.
Відомо, що вектори
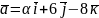 та
та
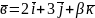 колінеарні. Знайдіть
і
.
колінеарні. Знайдіть
і
.
Розв'язання. Записуємо умову колінеарності заданих векторів:
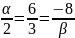
звідси
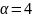 ,
,
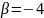 .
.
6.
Знайдіть подання вектора
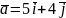 у базисі
у базисі
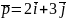 ,
,
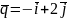 .
.
Розв'язання.
Передусім переконуємось, що вектори
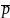 і
і
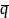 утворюють базис:
утворюють базис:
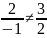 . Записуємо
розклад
. Записуємо
розклад
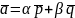 ,
де коефіцієнти
та
підлягають визначенню. Далі маємо
,
де коефіцієнти
та
підлягають визначенню. Далі маємо
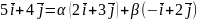
або
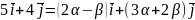
Звідси дістаємо систему рівнянь
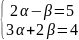 ,
,
розв’язок
якої
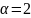 ,
,
 .
.
Отже,
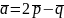 .
.
Вправи для аудиторної роботи.
1.
Дано точки
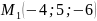 ,
,
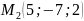 .
Знайдіть:
.
Знайдіть:
а) координати, довжину, напрямні косинуси та орт вектора ;
б)
координати точки М, яка ділить відрізок
у відношенні
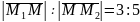 .
.
2.
Знайдіть вектор
,
якщо він утворює з осями Ох і Оу кути
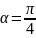 та
та
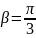 відповідно, і
відповідно, і
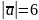 .
.
3.
Чи колінеарні вектори
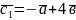 і
і
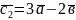 побудовані на векторах
побудовані на векторах
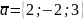 і
і
 ?
?
4.
Відомо, що вектори
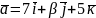 та
та
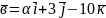 колінеарні. Знайдіть
і
.
колінеарні. Знайдіть
і
.
5.
Знайдіть подання вектора
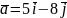 у базисі
у базисі
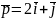 ,
,
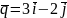 .
.
Самостійна робота № 8
Скалярний добуток векторів.
ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ.
Скалярним
добутком двох векторів
і
називають число
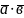 ,
що дорівнює добутку довжин цих векторів
на косинус кута між ними:
,
що дорівнює добутку довжин цих векторів
на косинус кута між ними:
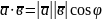
Якщо хоча б один із векторів чи нульовий, то за означенням
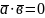 .
.
Оскільки виконуються рівності
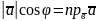 ,
,
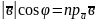
то
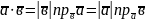
Геометричний зміст скалярного добутку: скалярний добуток двох векторів дорівнює добутку довжини одного вектора на проекцію на нього другого вектора (рис.1).
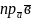
Тоді
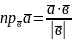 (1)
(1)
Формула (1) – робоча формула для обчислення проекції вектора на вектор (або вісь).
Властивості скалярного добутку.
Алгебраїчні властивості скалярного добутку:
1.
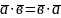 ;
;
2.
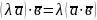 ;
;
3.
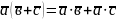 .
.
Геометричні властивості скалярного добутку:
1.
якщо
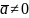 та
та
 , то
, то
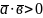 , якщо кут
гострий, і
, якщо кут
гострий, і
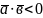 ,
якщо кут
тупий;
,
якщо кут
тупий;
2. скалярний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли ці вектори перпендикулярні;
3. скалярний квадрат вектора дорівнює квадрату його довжини, тобто
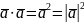 ,
,
звідки
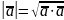 .
(2)
.
(2)
Умова перпендикулярності двох векторів.
Ненульові вектори і перпендикулярні тоді і тільки тоді, коли їхній скалярний добуток дорівнює нулю:
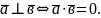
Зокрема:
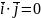 ,
,
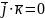 ,
,
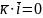
Вираз скалярного добутку через координати. Кут між векторами.
Нехай вектори і задані своїми координатами
, .
Тоді
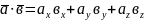 (3)
(3)
Висновки з формули (3) такі:
1. умова перпендикулярності векторів і :
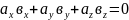 ;
;
2.
довжина вектора
:
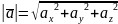 ;
;
3. косинус кута між векторами і :
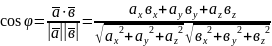 .
.
