Matematika_Praktikum

Общее решение ЛНДУ ищем в виде y C(x)sinx.

Найдем y C (x)sin x C (x)cos x .

Подставим у и y в исходное уравнение:

C (x)sin x C(x)cos x C(x)sin x ctg( x) sin( x)	или
C (x)sin x sin( x).

Получили C (x) 1 или dC(x) 1. Тогда C(x) dx x C .

dx

Следовательно, общее решение исходного уравнения есть y=(x+C) sin x.

II. Метод Бернулли

Пусть y uv. Тогда y u v uv и уравнение принимает вид

u v uv uv ctg x sin x ,

или

v(u uctg x) v u sin x .

Подберем функцию u(x) так, чтобы выражение в скобках равнялось нулю, т.е. решим первое дифференциальное уравнение с разделяющимися переменными u vctg x 0,

du uctg x, dx

ln	u	ln	sin x	ln	C1	, C1 0.
Откуда u=С1 sin x.
Пусть С1=1, u=sin x.
v sin x sin x, (по						условию sin x 0), отсюда	v 1, т.е.

v x C .

Итак, y=(x+C)·sin x, C R есть общее решение данного ЛНДУ.

№9. Найти общее решение уравнения	y			y
			x y2 .

Решение. Данное уравнение не является линейным

относительно х и x . Так как	y	1	, то приведем исходное
уравнение к виду (10.6):		х

101

y	1		y	, т.е. x	x y2	или x	x	y. Далее это ДУ
			x y2		y
	x						y

решим двумя методами:

1) Метод вариации произвольной постоянной

Найдем сначала общее решение соответствующего ЛОДУ

x x 0. Разделяя переменные и интегрируя, получим ln|x| =

y

ln |y| + ln |C1|, C1 0.

Общее решение ЛОДУ можно записать так х= Су, C R (так как х=0 – решение).

Общее решение заданного (преобразованного) уравнения ищем в виде х=С(у)у (постоянную С заменили неизвестной функцией С(у)). Подставляя х и x С (y)y С(y)в ЛНДУ,

придем к равенству:

C (y)y C(y) C(y)y y, т.е. y

C (y)y y.

Отсюда dC(y) 1, dC(y) dy. Интегрируя, имеем С(у) = у +

dy

С.

Таким образом, общее решение ЛНДУ есть х = (у + С)у или х = у2 + Су. Заметим, что у=0 также является решением, и для нашего примера оно является особым.

2) Метод подстановки

Полагаем x uv, где u=u(y), v=v(y) – функции переменной у. Подставим х и x u v uv в уравнение

u v uv 1 uv y или

у

				1		(*)
					v y.
u v u v
				у

Решим дифференциальное уравнение с разделяющимися

переменными v 1 v 0,

y

102

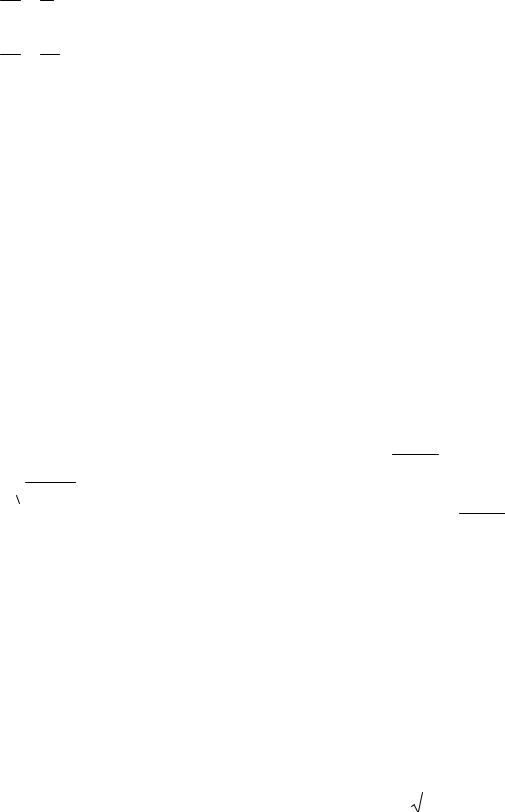
dv v , dy y

dv dy v y

откуда v=Cy, C R .

Выбираем одно из частных решений (самое простое), например, при С=1, т. е. v=y. Подставив v=y в уравнение (*), получим u y y или u 1. Тогда u = у + С. Следовательно, общее решение заданного уравнения х=у2+Су, C R , при этом у=0 – особое решение.

10.6. Варианты заданий

Уравнения с разделяющимися переменными

№10.1. Найти общие интегралы (общие решения)

уравнений.

а) (y 1)2 dx (1 x)3 dy 0;

б) x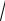9 y2 dx y(4 x 2 )dy 0 ;

в) cosxcosydx sinxsinydy 0; г) lnxsin3 ydx xcosydy 0;

д) xyy 1 x2 ;

е) sin dr 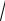r2 4 cos d 0;

ж)sin2 ytgxdx cos2 xctgydy 0;

з) (1 x2 ) y xy y1 x2 ;

и) y xy 2 0;

к) x 1 y2 dx ydy .

№10.2.

Найти

частные

решения

уравнений,

удовлетворяющие указанным начальным условиям:

а)

x

e;

y sin x y ln

y 0, y | e

ye

x 1,

y(1)

x

б)

;

2

r sin rlnr cos 0, r( /6) e;

е) x2dy y2dx, y(

1

)

1

;

в)

2

3

2

ж) y 1,5 3

,

y( 2)

1;

ydx (4 x

)ln y dy 0, y(2) 1;

y

з) 1 y2 xyy ,

1;

г)

y(2)

y 3x2

x 9 y 0,

y(0) 0;

и)

д)

y 2x y 2x y , y(0) 0 ;

к)

103

ds (3t 2 2t)dt , s |t 2 4 .

Однородные уравнения первого порядка

№10.3. Найдите общие решения уравнений:

у

а) ху у хех 0;

б) у ху у2 ; 2х2 ху

в) 2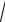ху х dy уdx 0;

г) ss 2s t 0;

д) у cos y у cos у 1 0; x x x

е) dу у x ;

dx x y

ж) y x у ; x y

з) xy y(ln y ln x) 0;

и) xy xtg у y; x

к) x2 y2 2xyy .

№10.4.

Найдите

частные

решения

уравнений,

удовлетворяющие указанным начальным условиям:

а)

x2 3y2

2xyy 0, y( 2) 2;

д)

dy

=

y

+sin(

y

),y(1)=π/

б)

xy2dy=(x3+y3)dx,

dx x

x

y(1)=3;

2;

в)

(x2+y2)dx=xydy,

е)

y

y

ln

y

,

y(1) e

y(1)=0;

x x

г)

(x – y)dy = y dx,

y(0)=1;

ж)

xcos(

y

)dy–

x

ycos( y )dx+xdx=0,

x

y(1)=0.

Линейные уравнения первого порядка

№10.5. Решить дифференциальные уравнения:

а) y	y	3 х ;	г)	dy	cos2		x y e tg x ;
				dx
	х
б) х2 y 2хy 1 0;				dy			y 2
в) y 7y 8е3х ;			д)					;
				dx			x ye 1 / y

104

x x0ekt.

е)	y tg х y			1		;	з) y	y	tg	x	;
				cosx				sin x	2
ж)	y 2	хy e	x		2		и) (x2 1)y xy x3 x.
					;

№10.6. Найти частные решения дифференциальных

уравнений,

удовлетворяющих

заданным

начальным

условиям:

а)

y 2y 1 2х2 , у(0) 2;

г)

xy y x3

0, y(2) 4;

б)

s ssint 2sin2t, s(0) 1;

д)

xy lnx y lnx, y(e2) 2ln2;

в)

1

dy

y sin x ycosx 1, y

е)

2

4

2

x dx y x

sin x, y( /2)

.

10.7. Применение дифференциальных уравнений в биологии и медицине.

Задача 1. Закон размножения бактерий с течением времени.

Скорость размножения некоторых бактерий пропорциональна количеству бактерий в данный момент. Найти зависимость изменения количества бактерий от времени.

Обозначим количество бактерий, имеющихся в данный момент, через х. Тогда

dx kx, dt

где k — коэффициент пропорциональности.

В этом уравнении разделим переменные и проинтегрируем его:

dx	kdt;		dx	k dt;	ln x kt lnC;
x			x

ln x lnekt lnC.

Потенцируем последнее выражение:

x Cekt.

Полагая, что при t=0 х=х0, получим С=x0. Следовательно,

(10.12)

Уравнение (9.7.1) выражает закон размножения бактерий с течением времени. Таким образом, при благоприятных условиях увеличение бактерий с течением времени происходит по

-

105

-

экспоненциальному закону.

Этот закон представляет интерес не только с теоретической, но и с практической точки зрения. Он говорит о том, что, создавая для полезной популяции благоприятные условия, можно очень быстро получить популяцию с больший численностью. Весьма показательна в этом смысле история с пенициллином. Когда был открыт этот антибиотик, грибки, его выделяющие, стали выращивать в наилучших условиях. Их неограниченно подкармливали, следили, чтобы им не было тесно, и, конечно, оберегали от вредных видов. Будущий урожай можно было совершенно точно подсчитать по формуле. Размножаясь в соответствии с экспоненциальным законом, пенициллиновые грибки в короткий срок обеспечили весь мир ценным лекарством.

Экспоненциальному закону размножения подчиняется так называемый «экологический взрыв», когда тот или иной биологический вид, попав В благоприятные условия, за короткий срок достигает большой численности. Для примера можно указать на губительные нашествия полчищ насекомых (саранчи, шелкопряда и др.) или на неожиданные последствия акклиматизации кроликов в Австралии.

Задача 2. Закон роста клеток с течением времени.

Для палочковидных клеток, у которых отношение поверхности клетки к ее объему сохраняется постоянным, скорость роста клетки dl/dt пропорциональна длине клетки l в данный момент:

dl ( )l,(10.13)

dt

где и β — постоянные, характеризующие процессы синтеза и распада.

В уравнении (9.7.2) разделим переменные и проинтегрируем его:

	dl	( )dt;		dl	( )dt;
	l			l
lnl ( )t lnC;			lnl lne( )t lnC,

l Ce( )t .

106

При t=0, l=l0 постоянная С=l0, и поэтому

l l0e( )t ,

т.е. рост палочковидных клеток происходит по экспоненциальному закону.

Задача 3. Закон разрушения клеток в звуковом поле.

Кавитация ультразвуковых волн проявляется в виде разрывов суспензионной среды и образования мельчайших пузырьков и пустот, плотность которых незначительна по сравнению с плотностью воды. Простейшие — бактерии, водоросли, дрожжи, лейкоциты и эритроциты — могут быть разрушены при кавитации, возникающей в интенсивном ультразвуковом ноле. В очень широком диапазоне частот относительные скорости разрушения биологических клеток различных видов остаются постоянными. Эти скорости могут характеризовать относительную хрупкость клеток различных видов. Чтобы выразить это количественно, нужно определить скорость разрушения клетки в постоянном звуковом поле. Изучение этого вопроса показывает, что, пока по крайней мере 1% популяции остается неразрушенным, можно написать, что

dN RN, (10.14)

dt

где N — концентрация клеток; t — время; R — постоянная. Разделим в уравнении (9.7.3) переменные и проинтегрируем

его:

	dN	Rdt;		dN	Rdt;	ln N Rt lnC;
	N
				N
		ln N ln e Rt lnC;				N Ce Rt.

Постоянную С найдем из условия, что при t=0 N=N0 и C=N0 Тогда

N N0e Rt

Разрушение клеток в постоянном звуковом поле происходит по экспоненциальному закону.

Задача 4. Составление и решение дифференциальных уравнений в теории эпидемий.

107

Рассмотрим составление и решение дифференциальных уравнений в теории эпидемий при условии, что изучаемое заболевание носит длительный характер. При этом процесс передачи инфекции значительно более быстрый, чем течение самой болезни, и зараженные особи не удаляются из колонии и передают при встречах инфекцию незаряженным особям.

Пусть в начальный момент t=0 a — число зараженных, b - число незаряженных особей, х(t)—число зараженных особей в момент времени t, a y(t) — число незараженных особей к моменту времени t.

В любой момент времени t для промежутка [0, Т], меньшего времени жизни одного поколения, имеет место равенство

x y a b. (10.15)

При этих условиях нужно найти закон изменения числа незараженных особей с течением времени, т. е. найти y=f(t).

Так как инфекция передается при встречах зараженных особей с. незараженными, то число незараженных особей будет убывать с течением времени пропорционально количеству встреч между зараженными и незаряженными особями. Для, промежутка времени dt

dy xydt,

Откуда

dy xy, dt

где β — коэффициент пропорциональности.

Подставив в это уравнение x из равенства (10.15), получим дифференциальное уравнение с разделяющимися переменными

dy y(a b y). dt

После разделения дифференциалов и переменных в последнем уравнении получим

dy

dt.

y(a b y)

Преобразуем левую часть уравнения и проинтегрируем его:

108

1

1

1

dy dt;

a b

a b y

y

1

1

1

dy

dt;

a b y

a b y

1

dy

1

dy

t C;

a b

a b y

y a b

ln y ln(a b y) (a b) t lnC

или

y

ln

ln e (a b)t lnC

a b y

Выполним в последнем уравнении потенцирование:

	y	Ce (a b)t.
	a b y

По начальным условиям: при t=0 y=b найдем постоянную интегрирования С:

	b	Ce0;	C	b
	a b b			a

Подставим значение С=b/a в последнее .равенство:

y		b	e (a b)t.
a b y
		a

Разрешая это уравнение относительно у, окончательно получим

	y(t)	b(a b)	.(10.16)
		b ae (a b)t

Формула (10.16) дает закон убывания числа незараженных особей с течением времени.

10.8.Варианты заданий

1.Скорость укорочения мышцы описывается уравнением

dx B(x0 x), dt

где х0 —полное укорочение мышцы; В — постоянная зависящая от грузки; х — укорочение мышцы в данный момент. Найти закон сокращения мышцы, если в момент времен t=0 величина укорочении мыший была равна 0.

2. Если при прохождении через слой воды толщиной 3 м поглощается половина первоначального количества света, то

109

какая то часть этого количества дойдет до глубины 30 м? Количество света, поглощенного при прохождении через топкий слой воды, пропорционально толщине слоя и количеству света, падающего на его поверхность.

3.Если первоначально количество фермента равно 1 г, а через 1 ч становятся равным 1,2 г, то чему оно будет равно через 5 ч после начала брожения? Скорость прироста фермента считать пропорциональной его наличному количеству.

4.Скорости ферментативных каталитических реакций иногда подсчитываются следующему уравнению:

dx k(a x) , dt 1 k'(a x)

где х- концентрация продукта в момент времени t: a - начальная концентрация реагента. Найти закон зависимости изменения концентрации продукта от времени.

5.Скорость распада некоторого лекарственного вещества пропорциональна наличному количеству лекарства. Известно, что по истечении 1 ч в организме осталось 31,4 г лекарственного вещества, а по истечении 3 ч – 9,7 г. Определить:

1)сколько лекарственного вещества было введено в организм:

2)через сколько времени после введения в организме останется 1% первоначального количества.

6.За 30 дней распалось 50% первоначального количества

радиоактивного вещества. Через сколько времени останется 1% от первоначального количества?

7.Определить период полураспада радия и радона, если

постоянные распада данных веществ соответственно равны

1,354·10-11с-1 и 2,1·10-6с-1.

8.Сколько ядер радиоактивного йода 53I131 из каждого миллиарда распадается в 1 с. если период, полураспада 53I131 равен 8 суткам?

9.Счетчик Гейгера, установленный вблизи препарата радиоактивного изотопа серебра, при первом изменении зарегистрировал 5200 (β-частиц в минуту, а через сутки — только

300.Определить период полураспада изотопа.

110